平移变换法速解圆锥曲线定点定值子弦问题

广东省广州市华南师范大学(510631) 王金莹

设点P是圆锥曲线上的一个定点,PA,PB是该曲线过定点P的两条弦,当直线PA,PB的斜率之和(积)为定值λ时,称线段AB为该曲线上定点P的关于定值λ的斜率等和(积)子弦[1].本文所研究的问题即圆锥曲线定点定值子弦的性质:当时,关于λ的斜率等和(积)子弦所在直线必过定点.

下面以椭圆为例,用平移变换法予以证明和应用.

一、斜率等和子弦

结论1椭圆C:= 1(a > b >0),点P(m,n)为椭圆C上一点.设直线l不经过点P,且与椭圆C相交于A,B两点.若kPA+kPB=λ(0),则直线l过定点.

证明作平移变换

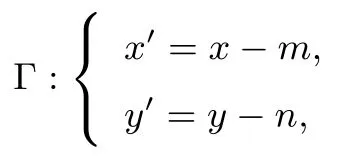
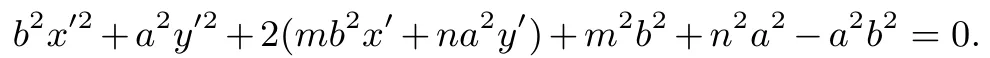
由于P(m,n)为椭圆上一点,所以.于是

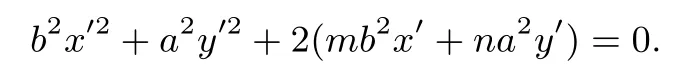
设l′:ux′+vy′=1,代入上式得

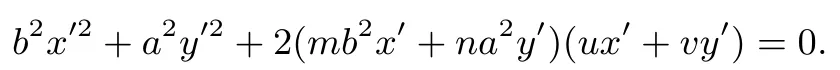
等式两边同时除以x′2得

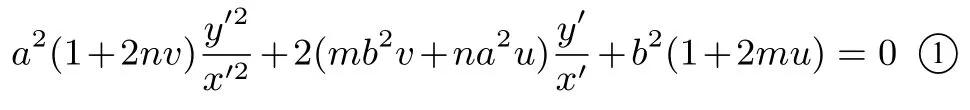
由于平移变换后点P的坐标变为P′(0,0),故kP′A′,kP′B′为方程①的两个根.又因为平移变换不改变直线的斜率,所以kP′A′+kP′B′=λ,从而由韦达定理有

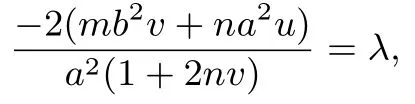
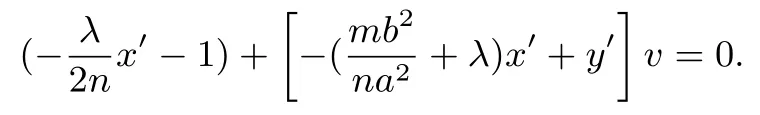
可知直线l′恒过定点,故直线l恒过定点

注利用平移变换,将椭圆上的定点转化为原点,从而变换后弦P′A′,P′B′的斜率即为点A′,B′的坐标比值.巧妙的是,平移变换不改变直线的斜率,而直线l不过定点P,也即变换后直线l′不过原点,故交点A′,B′必不是y轴上的点,如图1.由此可以同除以x′2得到方程①,kP′A′,kP′B′即为方程①的两个根,达到了简化运算,避免分类讨论不同直线情形的目的.

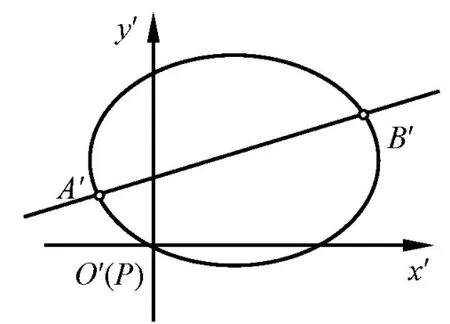
图1平移变换后的椭圆

例1(2017年高考全国I 卷理科第20 题)已知椭圆四点P1(1,1),P2(0,1),中恰有三点在椭圆C上.

(1)求椭圆C的方程;

(2)设直线l不经过点P2且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为−1.证明:直线l过定点.

证明(1)

(2)作平移变换

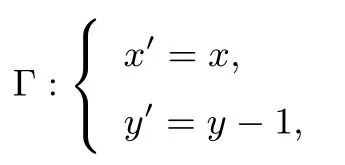
设l′:mx′+ny′=1,代入上式得

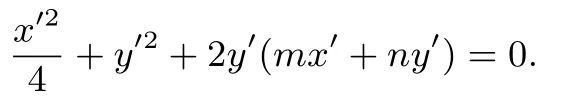
等式两边同时除以x′2得

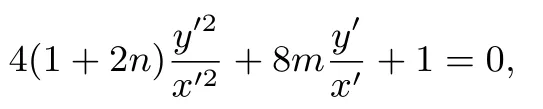
可知kP2′A′,kP2′B′为方程的两个根.又因为平移变换不改变直线的斜率,所以kP2′A′+kP2′B′=−1,从而由韦达定理有−=−1,化简得2m= 1+2n,代入直线l′方程得故直线l′过定点(2,−2).从而由变换Γ 知直线l过定点(2,−1).

评注常用的证明方法需要设直线斜截式与曲线联立,于是需要讨论斜率的存在性.此外,kP2A+kP2B的坐标表示非常复杂.而利用平移变换则解决了以上难处,寥寥几行便得知直线所过的定点.

例2(2015年高考陕西卷文科第20 题)椭圆E:经过点A(0,−1),且离心率为

(1)求椭圆E的方程;

(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.

解(1)

(2)作平移变换

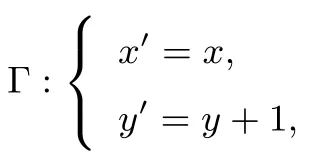
设l′:mx′+ny′= 1,由于平移变换不改变直线斜率,且点(1,1)变换后为(1,2),从而直线l′方程为(1−2n)x′+ny′=1,代入椭圆方程得

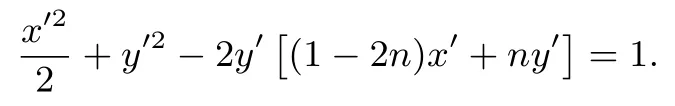
等式两边同时除以x′2得

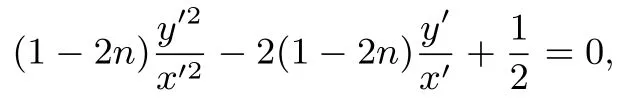
可知kP2′A′,kP2′B′为方程的两个根,故

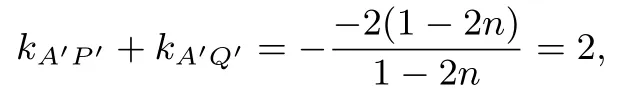
也即kAP+kAQ=2.

例3(2018年中原名校高三第六次质检)已知椭圆的离心率,且椭圆C与圆的4 个交点恰为一个正方形的4 个顶点.

(1)求椭圆C的标准方程;

(2)已知点A为椭圆C的下顶点,D,E为椭圆C上与A不重合的两点.若直线AD与直线AE的斜率之和为a2,试判断是否存在定点G,使得直线DE恒过点G.若存在,求出点G的坐标;若不存在,请说明理由.

解(1)

(2)作平移变换

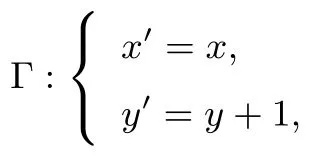
设l′:mx′+ny′=1,代入上式得

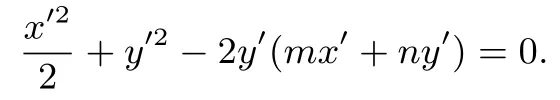
等式两边同时除以x′2得

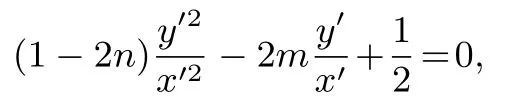
可知kP2′A′,kP2′B′为方程的两个根,从而由韦达定理有kA′D′+kA′E′== 2,化简得m= 1−2n,代入直线l′方程得(−2x′+y′)n+x′−1 = 0,故直线l′过定点(1,2).从而由变换Γ 知直线l过定点(1,1).

评注例2 和例3 互为逆命题,可知斜率等和(积)与子弦所在直线过定点是等价关系.

二、斜率等积子弦

结论2椭圆C:= 1(a > b >0),点P(m,n)为椭圆C上一点.设直线l不经过点P,且与椭圆C相交于A,B两点.若则直线l过定点.

证明同结论一证明得方程

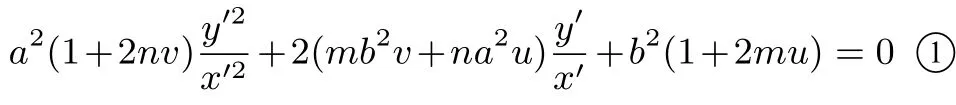
同理可知kP′A′,kP′B′为方程①的两个根且kP′A′·kP′B′=λ,故由韦达定理有

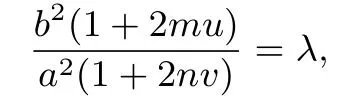
化简得

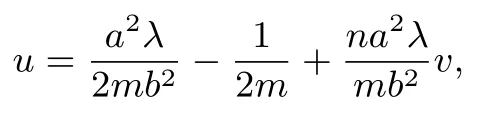
代入直线l′方程得

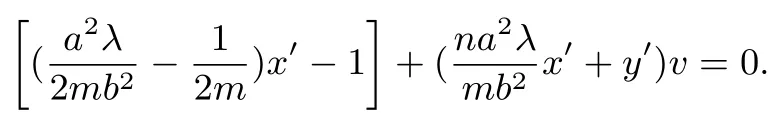
可知直线l′恒过定点故平移变换前直线l恒过定点

例4(2019年昆明市教学质检)已知椭圆C的中心在原点,一个焦点为,且椭圆C经过点

(1)求椭圆C的方程;

(2)设椭圆C与y轴的正半轴交于点D,直线l与椭圆C交于A,B两点(l不经过点D),且AD⊥BD.证明:直线l经过定点,并求出定点的坐标.

解(1)

(2)依题意可知D(0,1),kAD·kBD=−1.作平移变换

同例1可得方程

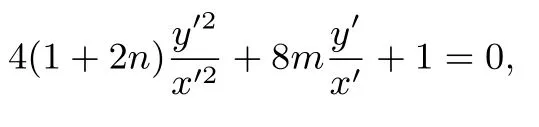
kA′D′,kB′D′为方程的两个根.因为平移变换不改变直线的斜率,从而,解得于是直线l′的方程为,可知直线l′过定点从而由变换Γ 知直线l过定点

评注本题与例1 几乎一致,差别不过是对方程利用韦达定理求两根之积,可见这一方法的普适性.同时也提醒我们,许多试题都是同源的,要勤于钻研,举一反三.

例5(2016年宜昌市模拟考试)已知椭圆C的中心在原点,焦点在x轴上,离心率为,它的一个焦点恰好与抛物线y2=4x的焦点重合.

(1)求椭圆C的方程;

(2)设椭圆的上顶点为A,过点A作椭圆C的两条动弦AB,AC.若直线AB,AC斜率之积为,直线BC是否恒过一定点?若经过,求出该定点坐标;若不经过,请说明理由.

解(1)

(2)依题意可知A(0,1),作平移变换

设l′:mx′+ny′=1,代入上式得+y′2+2y′(mx′+ny′)=0.等式两边同时除以x′2得

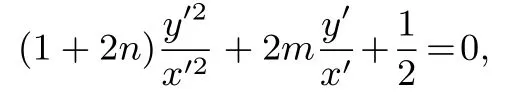
可知kA′B′,kA′C′为方程的两个根,从而由韦达定理有kA′B′+kA′C′=,化简得,代入直线l′方程得,故直线l′过定点(0,2).从而由变换Γ 知直线l过定点(0,3).

三、结束语

解析几何常常因为大量的计算影响解题速度,让学生产生畏难情绪.除了上述的平移变换法,还有伸缩变换法、极坐标法、参数方程法等等灵活计算的方法,可以大大降低计算量,掌握这些技巧是挖掘解析几何各种性质的有利武器.