2019年全国I卷理科第21题的探究及其题型归类

广东省湛江一中培才学校(524037) 魏 欣

课堂教学活动要以教材为准则,解题教学要以课本例习题为基础,并作合理变式,适度拓展,充分发挥例习题所蕴含的数学问题的典型性、方法的指导性、解题过程的示范性作用.下面以2019年全国Ⅰ卷理科第21 题为例,挖掘教材和高考题的功能,探究求满足an+2=pan+1+qan(n ∈N∗)的二阶线性递推数列通项公式的解法.

一、试题展示与评析

题目(2019年全国Ⅰ卷理科第21 题)为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1 分,乙药得−1 分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1 分,甲药得−1 分;若都治愈或都未治愈则两种药均得0 分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.

(Ⅰ)求X的分布列;

(Ⅱ)若甲药、乙药在试验开始时都赋予4 分,pi(i=0,1,··· ,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则

p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,··· ,7),其中a=P(X=−1),b=P(X= 0),c=P(X= 1).假设α=0.5,β=0.8.

(i)证明:{pi+1−pi}(i=0,1,2,··· ,7)为等比数列;

(ii)求p4,并根据p4的值解释这种试验方案的合理性.

解(Ⅰ)X的所有可能取值为−1,0,1;

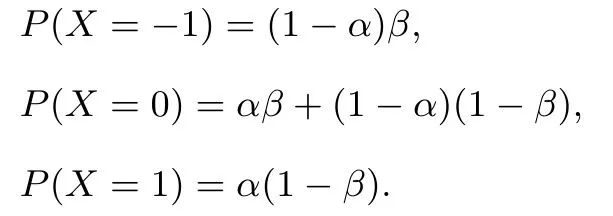
所以X的分布列为:

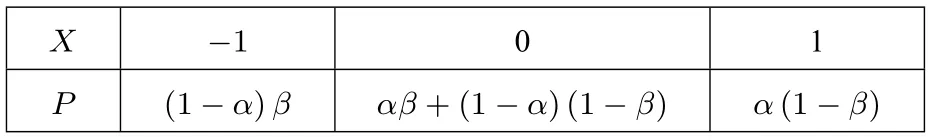
X−1 0 1P(1−α)βαβ+(1−α)(1−β)α(1−β)

(Ⅱ)(i)由(1)得a= 0.4,b= 0.5,c= 0.1.因此pi=0.4pi-1+0.5pi+0.1pi+1,所以0.5pi= 0.4pi-1+0.1pi+1,故pi+1=5pi−4pi-1,即pi+1−pi=4(pi−pi-1).又因为p1−p0=p1≠ 0,所以{pi+1−pi}(i= 0,1,2,··· ,7)为公比为4,首项为p1的等比数列.

(ii)由(i)可得

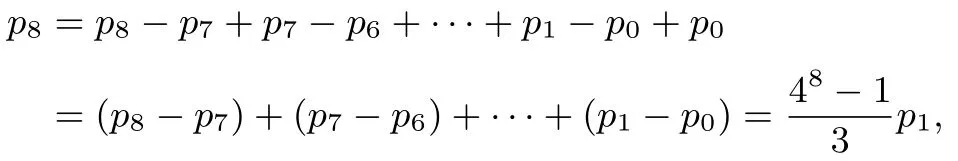
由于p8=1,故,所以

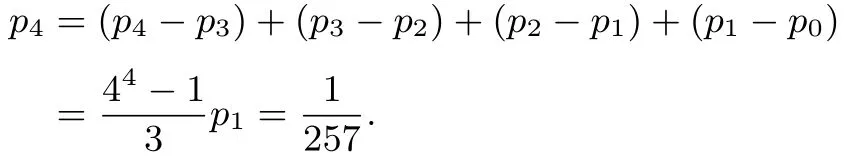
p4表示最终认为甲药更有效的概率,由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8 时,认为甲药更有效的概率为,此时得出错误结论的概率非常小,说明这种试验方案合理.

评析本题在试卷中处于21 题,属于压轴题的位置,该题以测试新药为背景,解释试验方案的合理性,是一个数学应用的题目,体现了数学的应用价值,考察了学生的数学建模能力与数据分析能力.此外,本题第二问还考察了数列方面的知识,要求学生有较强的分析能力与推理能力,因此本题综合性较强,是一道考察学生数学综合能力的好题.

二、教材寻根

在解答过程中,有pi+1= 5pi−4pi-1,实质上是求二阶线性递推数列的通项公式.考查数列的相关知识,重点考查概率与数列知识,知识点全面,数学思想丰富,运用到化归与转化、数学建模等数学思想方法,能充分检测学生对相关知识的掌握程度,以及运用数学知识解决问题的能力.既有初等数学背景,又有高等数学特征方程、特征根的影子,是初等数学与高等数学完美结合的一个典型.深入研究,可以在教材中找到此题的“题根”.

题目(新课标人教版A 版《数学(必修5)》第二章复习参考题B 组第6 题)已知数列{an}中,a1=5,a2=2,an=2an-1+3an-2(n≥3),对于这个数列的通项公式作一研究,能否写出它的通项公式?

解法1(配凑法)由an=2an-1+3an-2,得

而a2−3a1=−13,故数列{an+1−3an}是公比为−1,首项为−13 的等比数列,所以

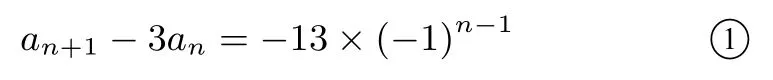
又由an=2an-1+3an-2,得an+an-1=3(an-1+an-2),而a2+a1=7,故数列{an+1+an}是公比为3,首项为7 的等比数列,所以

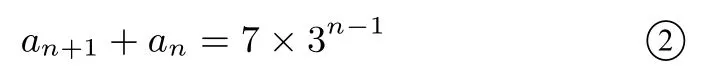
由①、②两式消去,得

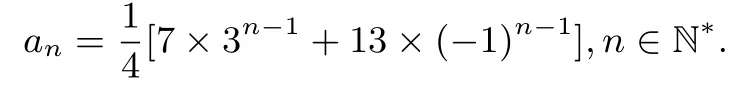
解法2(待定系数法)由an=2an-1+3an-2,设

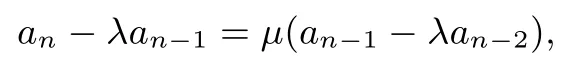
其中λ,µ是待定的常数,则

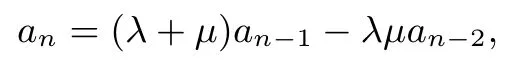
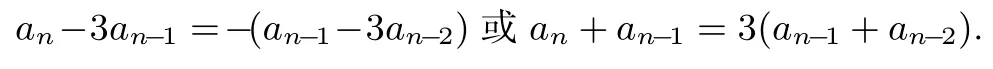
下面与解法一相同,可得

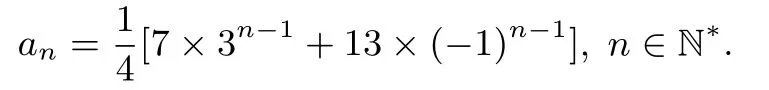
小结G•波利亚曾说:观察可能导致发现.观察将揭示某种规律、模式或定律.通过比较,我们发现解法1 和解法2的解法本质上是相同的,关键是构造出两个等比数列,再利用方程思想得到通项公式.这种解法能否推广到一般情况呢?是否都能构造出两个等比数列呢?回答是肯定的.

三、提炼推广

问题的提炼设数列{an}满足:a1=a,a2=b,an+2=pan+1+qan,n ∈N∗,(pq≠0),求an.

解设an+2−λan+1=µ(an+1−λan),其中λ,µ是待定的常数,则an+2= (λ+µ)an+1−λµan,比较系数得显然λ,µ是方程x2−px −q=0 的两根,即方程x2=px+q的两根,

当∆=p2+4q≥0 时,设其实根为α,β,从而有得an+2−αan+1=β(an+1−αan)或an+2+βan-1=α(an+1+βan),所以数列{an+1−αan},{an+1−βan}分别是公比为β和α的等比数列,故得

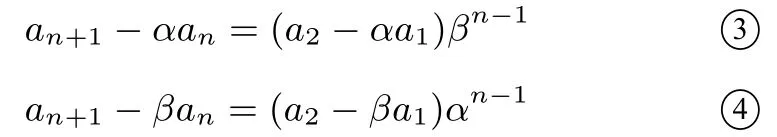
(ⅰ)当时,由 ③−④消去an+1,可得an,即

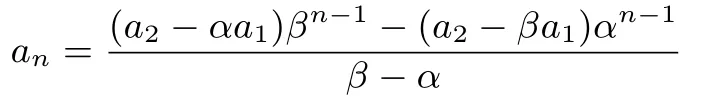
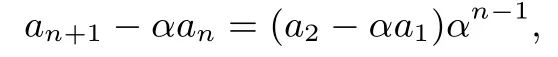
上式两边同除以αn+1,得

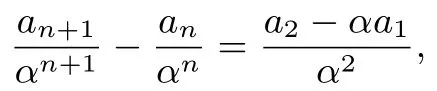
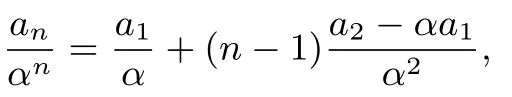
得

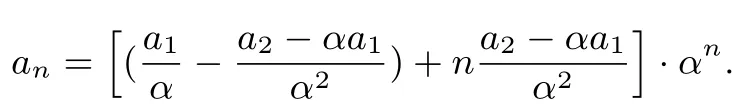
从上述解答过程来看,我们不仅找到了解决问题的方法,而且找到了解决问题的公式.正如教育家G•波利亚所说的一样,“好问题同某种蘑菇有些相像,它们都成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个”.

解法小结上述解题过程中得到的方程x2=px+q称为递推方程an+2=pan+1+qan的特征方程,特征方程的根α,β叫做特征根.

设数列{an}满足:a1=a,a2=b,an+2=pan+1+qan,n ∈N∗,(pq0),其特征方程为x2=px+q,设其两根为α和β.

构造法结论1:二阶线性递推数列的通项公式均可通过构造法转化为等比数列或等差数列求得.构造过程可采用配凑法、待定系数法.

(ⅰ)当方程有两个相异实根()时,构造两个等比数列{an+1−αan},{an+1−βan},它们的公比分别为β和α,再利用方程思想解得通项an.

(ⅱ)当方程有两个相同实根(α=β)时,可以构造出等差数列,其公差为,首项为的等差数列.

待定系数法结论2:

(ⅰ)当方程有两个相异实根(αβ)时,an=c1αn-1+c2βn-1,常数c1,c2由a1,a2确定;

(ⅱ)当方程有两个相同实根(α=β)时,an=(c1+nc2)αn,常数c1,c2由a1,a2确定;

(ⅲ)当方程有两个共轭复数根时,an=c1αn-1+c2βn-1,常数c1,c2由a1,a2确定.

由此,对于例2,可得

解法3(待定系数法)由an= 2an-1+3an-2,得特征方程为x2= 2x+3,解得x1= 3,x2=−1,设an=c1×3n-1+c2×(−1)n-1,其中c1,c2是待定的常数,把a1=5,a2=2 的值代入得

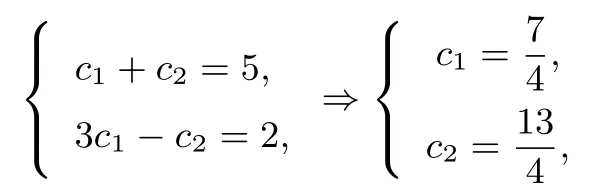
从而

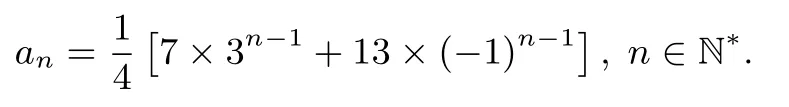
四、题型归类

类型一:特征方程有两个相等实根

例1(2009 全国II 卷理科第19 题)设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2.

(1)设bn=an+1−2an,证明数列{bn}是等比数列;

(2)求数列{an}的通项公式.

分析由已知Sn+1=4an+2,得Sn+2=4an+1+2,两式相减得:an+2= 4an+1−4an,可直接应用特征根法就数列{an}的通项公式.

解由已知Sn+1= 4an+2,得Sn+2= 4an+1+2,两式相减得:an+2= 4an+1−4an,特征方程是x2= 4x −4,x1=x2=2,

设an=(c1+nc2)2n,又a1=1,a1+a2=S2=4a1+2,得a2=5.把a1=1,a2=5 代入通项公式,得

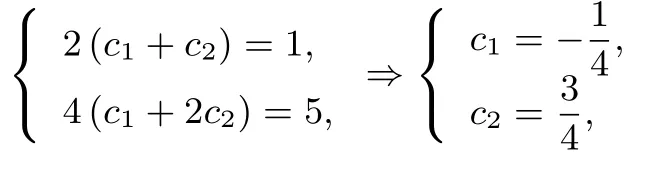
故

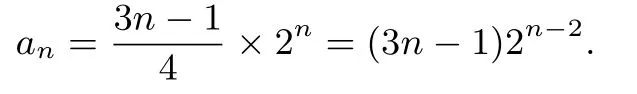
例2(2013年高考安徽卷文科第19 题)设数列{an}满足a1=2,a2+a4=8,且对任意n ∈N∗,函数

(1)求数列{an}的通项公式;(2)略.

解f′(x)=an−an+1+an+2−an+1sinx−an+2cosx,an−an+1+an+2−an+1= 0,即an+2= 2an+1−an,显然可以利用特征根法求解.又an+2= 2an+1−an可变形为2an+1=an+an+2,从而知数列{an}是等差数列,由已知可得公差为1,且首项a1=2,所以an=n+1.

注当p=2,q=−1 时,满足an+2=pan+1+qan的数列{an}是等差数列.

类型二:特征方程有两个相异实根

例3(2008年高考广东卷文科第21 题)设数列{an}满足a1= 1,a2= 2,an=(an-1+2an-2),(n= 3,4,···).数列{bn}满足b1=1,bn(n=2,3,4,···)是非零整数,且对任意的正整数m和自然数k,都有:−1 ≤bm+bm+1+···+bm+k≤1.

(1)求数列{an}和{bn}的通项公式;(2)略.

解特征方程是设把a1=1,a2=2 代入通项公式,得

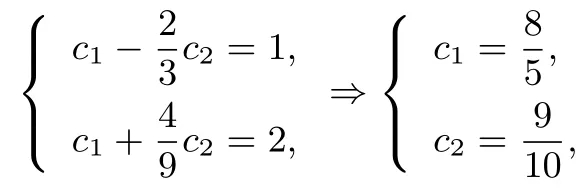
例4(2010年全国高中数学竞赛河北赛区第6 题)从满足a1=a2= 1,an+2=an+1+an(n≥1)的数列{an}中,依次抽出能被3 整除的项组成数列{bn},则b100=( ).

A.a100B.a200C.a300D.a400

解此数列是斐波那契数列,写出前几项,归纳可知a4k(k≥1)能被3 整除,故选D.

设

把a1=a2=1 代入通项公式,得

故

启示“斐波那契数列”是人教A 版《数学(必修5)》第二章第一节的阅读材料,教材中给出了递推关系式,但没有给出通项公式,我们在教学中,可以适当地对相关知识进行拓展、延伸,对学生的成长会有很大的促进作用.

类型三:特征方程有两个共轭复数根

例5(2013年全国高中数学竞赛安徽赛区第4 题)设数列数列{an}满足a1=a2= 1,an=−an-2(n≥3),则a2013=____.

解特征方程是,得两根为

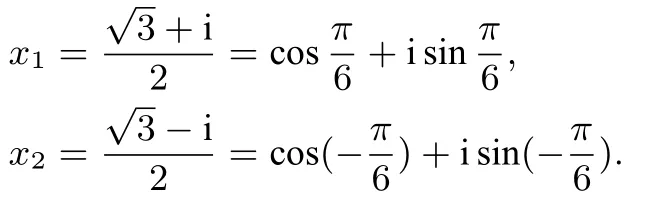
设

把a1=a2=1 代入通项公式,得

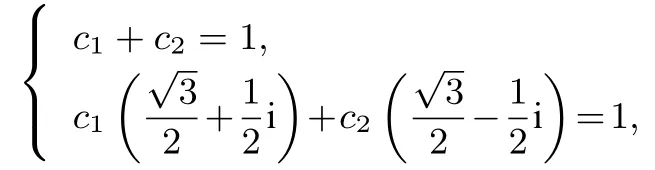
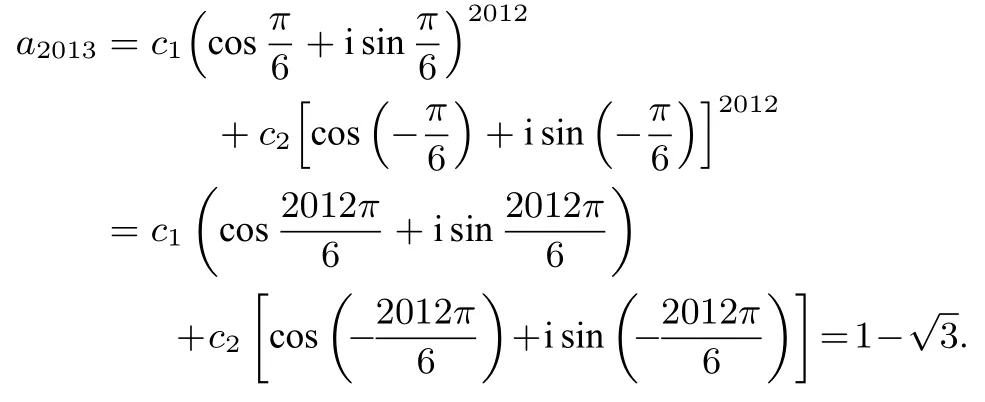
五、教学建议

教材是教师上课之本、学生数学认知之本,也是高考专家命题之本.分析教材是教师进行教学设计的基础,是教师上课的前奏;对教材分析是否到位,不仅关系到能否真正发挥教材的作用,也会直接影响教师的课堂教学质量.其中,课本例题与习题也是需要教师尤为关注的对象,课本例题既是如何运用知识解题的经典,也是思维训练的典范.习题则是例题的题型与模式在学生头脑中的再现,是对学生知识与方法掌握与否的考查.例题的教学与习题的训练是整个教学活动的重要部分,下面就教师在教学过程对教材例题与习题的处理提一些建议.

1 仔细分析,注重例题中隐含的数学思想方法.

掌握数学思想方法是掌握解决数学问题的本质,教师除了向学生展示例题的解决过程,更应该注重提取例题背后隐含的数学思想方法,并让学生学会对方法进行总结和迁移.学生不仅知道如何解这道题,而且能从中学习解决此类问题的技能,能以点化面,举一反三.

2 理解例题结论,构建模式题型.

教材中的某些例题,除了是本节知识点的应用典范外,其结论的呈现可能具有一定的目的和意图.学生具有例题结论的经验,在头脑中形成模式化,可能对后续问题的解决具有较好的指引作用.然而大部分学生这种挖掘例题背后意图的能力不足,需要教师的适当引导与启发.

3 立足学生认知,合理进行归类总结及其变式.

基于例题思想方法的典型性,将例题进行变式训练是促进学生知识迁移的一个必要环节.在对例题进行变式时,我们应注重立足学生的数学认知,在原有认知的基础上进行有意义的拓展延伸.为了让学生从原有认知顺畅地过渡到拓展的结论,可以适当地运用图形直观,使学生意识到拓展结论的合理性,引发学生想办法证明结论的兴趣.同时作一个较为系统的梳理和总结,以期达到让学生能抓住重点的同时又突破难点的目的.