考虑柱纵向钢筋屈曲特征的修正材料本构模型

杨 红，耿南锋，刘子珅

(1.重庆大学土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400030)

震害现象和试验结果表明[1-4]，纵向受力钢筋屈曲是混凝土柱受力后期的重要非线性特征之一。屈曲是指钢筋受拉屈服并经历一定塑性伸长后，反向受压时逐渐弯曲并向外鼓出，且纵筋的弯曲程度随柱顶侧移变形加大而逐渐加重，保护层混凝土剥落后甚至可观察到纵筋在塑性铰区反复压弯、拉直的现象。纵筋屈曲会导致钢筋混凝土柱抗震性能退化、承载能力降低，严重时可能引起构件失效，并使构件的修复、加固极为困难[1,4]。

将构件控制截面按纤维进行离散化是目前计算钢筋混凝土结构、构件非线性反应的常用细化有限元分析方法，此时，必须分别采用合理的单轴材料本构模型准确描述混凝土、钢筋的滞回受力性能[4-6]。对于屈曲钢筋，采用纤维模型进行分析时一般通过将弯曲的钢筋视为未弯曲的等效单轴材料，同时修正钢筋应力-应变模型以考虑屈曲效应的影响。因此，建立能正确反映屈曲导致的局部非线性特征影响的钢筋等效材料本构模型是有限元计算结果真实、合理的基础。

一些学者对钢筋的屈曲受力性能进行了研究。Monti 等[7]、Rodriguez 等[8]、Bae 等[9]、Kashani 等[10]通过单根钢筋的单调或循环加载试验研究了长径比、初始偏心等因素对钢筋屈曲受力性能的影响；Dhakal 等[11]采用细化有限元法研究了长径比、屈服强度对屈曲的影响；Zong 等[12]采用“弹簧支承梁”模型分析了初始缺陷、箍筋强度、纵筋屈服强度等的影响。

在试验、有限元分析结果的基础上，研究者普遍采用的考虑纵筋屈曲影响的简化方法是[7,11,13-19]，根据屈曲纵筋在相邻两层箍筋之间的轴向力P、轴向变形δ分别计算钢筋的平均应力(σ=P/As，As为钢筋的名义截面面积)、平均应变(ε=δ/L，L为屈曲钢筋的初始长度)，并通过修正σ-ε关系以近似考虑屈曲对钢筋本构模型的影响(即将屈曲钢筋等效为未弯曲的单轴材料)。Monti 等[7]根据试验结果提出的模型计算公式较复杂；Dhakal 等[11]建立的考虑长径比、屈服强度影响的模型仅适用于单调加载；Gomes和Appleton[13]提出的模型力学概念清楚，但模拟效果差(以下称G-A 模型)；Akkaya 等[14]在文献[11]的基础上提出了改进模型并对其进行了验证；OpenSees 中的Reinforcing Steel 单轴材料本构模型[15]通过引入β、r和γ三个参数对G-A 模型进行了改进，但其参数β在程序中被固定为1.0(无法调节屈曲开始点的位置)；Kunnath 等[16]建议的修正模型无法考虑屈服强度对应力-应变关系的影响；杨红等[17]为提高使用效率对Reinforcing Steel 模型进行了改进；文献[18]通过改进屈曲力学模型提出了修正的G-A 模型；Urmson 等[19]通过分析屈曲钢筋中间截面的弯矩表达式(以应变比 y/ε ε和长径比L/d为变量)，对屈曲受压的平均应力-平均应变骨架曲线进行了修正。此外，刘子珅等[20]对屈曲钢筋的变形特征进行了分析，提出了三种基于横向挠度判断钢筋屈曲开始点的方法。邢国华等[21]研究锈蚀钢筋混凝土柱的压-剪-弯修正有限元模型时考虑了纵筋屈曲效应的影响。

以上各种考虑屈曲影响的钢筋材料本构模型多是基于试验结果建立σ-ε的经验公式，或是对数值分析结果进行现象学总结获得σ-ε的简化曲线，且文献[17－18]直接采用G-A 模型的两个基本假定，均缺乏受力机理分析。本文以G-A 模型为基础，通过对钢筋屈曲受力模型各基本假定的合理性、误差进行分析，从变形、受力特征出发建立了力学概念明确、模拟效果更优的考虑屈曲影响的钢筋材料本构模型修正方法。

1 屈曲钢筋的循环加载试验 与有限元模拟

文献[17]完成了36 个原状钢筋试件(测试段未进行任何加工处理)考虑屈曲的循环拉压试验，本文首先采用基于截面纤维模型和非线性杆单元的有限元模型对各试件的试验进行了模拟。

1.1 试验方法

各试验均在INSTRON 电液侍服单轴材料试验机(如图1(a)所示)上完成。各钢筋试件直径分别为 12 mm、14 mm、16 mm、18 mm、20 mm、22 mm共6 种；试件的试验段长度分别为100 mm、 150 mm共2 种，共进行了36 个试件的屈曲受力性能试验。

试验采用的三种加载方法分别为：“拉-压相等循环加载”和“拉-压不等循环加载”(分别反映不同轴压比时柱纵筋的受力特征)、完全受拉的“拉-拉循环加载”(反映梁纵筋的受力特征)。由于研究对象为柱纵筋，故本文仅分析拉-压相等、拉-压不等的24 个试件。

各试件均采用位移控制加载，直至钢筋断裂。试验过程中，通过传感器采集了INSTRON 试验机对试件施加的轴向力P，采用百分表分别测量了屈曲钢筋沿竖向的长度变化量ΔL、 钢筋跨中截面的横向屈曲位移(见图1(b))。

图1 试验装置与屈曲钢筋的横向屈曲位移测量方法 Fig.1 Testing equipment and lateral buckling displacements measuring method of buckled steel bars

1.2 屈曲钢筋的简化力学模型与有限元模拟方法

观察图2(a)发现，屈曲后钢筋构件可视为由中间截面分开的上、下两根杆件，塑性变形和损伤主要集中在杆件两端，符合集中塑性铰模型的受力特点(见图2(b))。因此，参考Dhakal 等[11]以及Massone等[22]的做法，将屈曲钢筋简化为由跨中截面分开的两个集中塑性铰杆单元，如图2(c)的“单元1”和“单元2”所示。

图2 屈曲钢筋有限元模型示意图 Fig.2 Schematic of FEM model of a buckled steel bar

图2(c)的有限元模型中，单元1 和单元2 均采用OpenSees 中的Beam With Hinges Element 模拟，单元中部定义为弹性，单元端部的p1l和p2l为塑性铰长度，根据各试件的损伤特点，结合Massone 等[22]和Scott 等[23]的建议，计算时取lp1=lp2= 5d/6 (d为钢筋的初始直径)。

两单元端部控制截面采用纤维模型定义，各纤维均采用OpenSees 中的Reinforcing Steel 材料模型。模型通过杆件大变形模拟钢筋的屈曲受力特征，故定义Reinforcing Steel 材料模型时疲劳参数、屈曲参数均取为0。

1.3 有限元计算结果

图3 为部分钢筋试件的σ-ε试验结果与有限元计算结果对比，图中试件D12-150-1 的编号含义为：钢筋直径为12 mm、自由段长度为150 mm、试验采用第一种加载方法(即拉-压相等循环加载)，其他试件类似。由图3 可见OpenSees 的模拟结果误差小，这确保了有限元计算结果的合理性。有限元模拟存在的主要误差是在后期的循环加载过程中与最大拉应变对应的平均应力值略大于试验实测结果，主要是由于Reinforcing Steel 材料本构的疲劳参数已设为0，未考虑钢筋因低周疲劳损伤导致的强度衰减。

图3 钢筋试件σ-ε 曲线的试验与有限元计算结果对比 Fig.3 Comparison of experimental and computational σ-ε curves of steel bar specimens

图4 为部分试件跨中截面的横向屈曲位移的有限元计算结果与试验测量结果对比，两者的曲线形状、峰值和谷值大小基本相同，这进一步证明了有限元模拟结果的有效性。因此，有限元计算得到的每循环最大拉、压平均应变对应的中间节点侧向位移值较为准确(与试验结果相比差异小)，说明该有限元模型可以较真实地再现随着加载位移幅值增大(或横坐标“数据采集点序列”逐渐加大)，钢筋中间节点的侧向位移峰值不断增大(或钢筋弯曲程度逐渐加重)的特征。

图4 钢筋试件屈曲横向位移曲线试验与计算结果对比 Fig.4 Comparison of experimental and computational lateral buckling displacement curves of steel bar specimens

2 G-A 模型的计算公式与基本假定

G-A 模型[13]有明确的力学概念，故本文以G-A模型为基础对屈曲钢筋的σ-ε模型进行改进。

如图5 所示，G-A 模型是以相邻两箍筋之间纵筋屈曲后的塑性机构平衡为基础建立的简化理论分析模型，图中L为钢筋的初始长度，δ为钢筋端部纵向位移，θ为刚性转角，w为中间节点的横向位移。

图5 屈曲纵筋的受力平衡关系[13] Fig.5 Equilibrium relationship of a buckled bar[13]

忽略钢筋轴向变形，w、δ和θ之间的几何关系为：

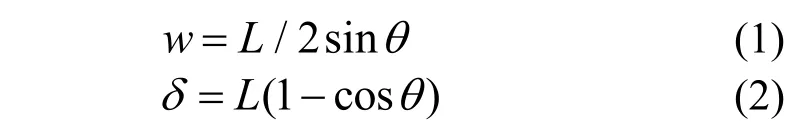
忽略高阶无穷小项，由式(1)和式(2)可得：

G-A 模型假定屈曲钢筋的塑性变形全部集中在端部截面与中间截面，且均为全截面塑性状态，式中Mp为钢筋的截面塑性弯矩。将钢筋视为圆形截面并忽略轴力作用，可以得到：

式中：Zp为截面的塑性模量；σy为钢筋的屈服强度；d为钢筋直径。

由式(4)和式(5)可得：

将相邻箍筋间屈曲纵筋的平均应变定义为ε=δ/L，平均应力定义为σ=P/As，则不考虑轴力影响时有：

将式(7)用于整体σ-ε关系曲线时，其中的应力是以零应力点为参考的，即ε-ε0，其中ε0为零应力点处的应变。因此，σ-ε关系可变换为：

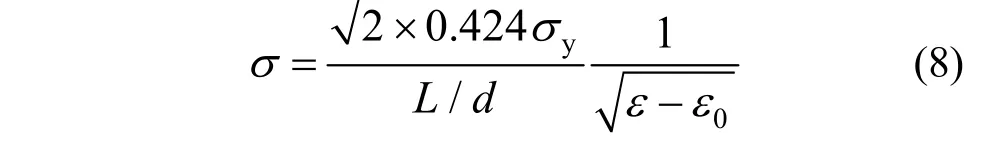
如果计算屈曲钢筋中间截面塑性弯矩时考虑轴力的作用，则可以得到：

故考虑轴力的平均应力-平均应变关系为：

Gomes和Appleton[13]通过比较考虑和不考虑轴力与弯矩间相互作用时的σ-ε骨架曲线发现，ε较小时两种方法的计算结果有一定差别，但ε较大时差别很小。因此原始G-A 模型采用了式(8)所示的简化关系。

式(8)为G-A 模型给出的屈曲钢筋应力计算表达式的初始形式，为方便程序编制，一般可将其改写为式(12)，其中Ω为原始G-A 模型的比例系数。

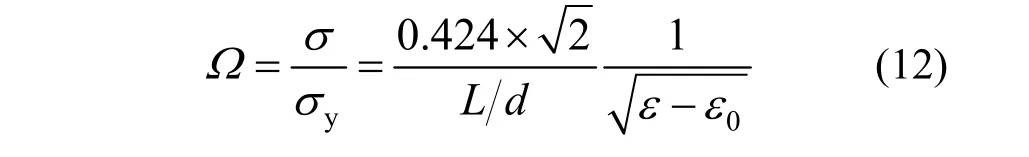
3 原始G-A 模型几何关系的修正

3.1 对G-A 模型几何关系的第一种修正方法

以处于图6(a)所示某屈曲状态的钢筋为例，其顶端竖向位移δ、杆件轴向变形ε′均会引起中间节点侧向位移，同时考虑两类贡献的中间节点侧向位移在图6 中用w′表示，并用Δw表示单元轴向变形对中间节点侧向位移的影响。如图6(b)所示，若不考虑轴向变形、仅在δ作用下，中间节点将产生侧向位移GAw-(这即是G-A 模型的几何关系基本假定)。在图6(b)基础上进一步考虑单元轴向变形ε′影响，若杆件承受压力，单元长度缩短将导致GAw-减小至w′，则wΔ 为负，如图6(c)所示；若单元承受拉力、杆件长度伸长，将导致GAw-增加至w′，则Δw为正(见图6(d))。因此，可用 Δw/w0表示ε′对中间节点侧向位移w0的贡献。

图6 中间节点侧向位移的构成示意 Fig.6 Composition of lateral displacement of mid-span node

提取各试件的有限元计算结果后，可按式(12)～式(14)计算 0/w wΔ ，其中0w为图2(c)所示有限元模型中间节点2 的侧向位移的数值计算结果。

根 据 计 算 结 果 绘 制ε/εy- Δw/w0和ε/εy-wG-A/w0关系曲线，结果如图7 所示。可见，两试件的 Δw/w0和wG-A/w0随应变比ε/εy的变化规律是类似的，当ε/εy较小时，Δw/w0为负值，且绝对值很大，说明屈曲钢筋轴向压缩使跨中侧向位移在GAw-的基础上明显减小；随着加载的进行(y/ε ε增大)，ε′对0w的影响逐渐减小，顶端节点的竖向位移δ(或平均应变ε)成为决定0w的主要因素。与D20-100-1 相比，试件D20-100-2 的 0/w wΔ由负值转为正值所对应的 y/ε ε更小。

图8 为拉-压相等、拉-压不等循环加载下典型试件的 y/ε ε-0/w wΔ 关系计算结果汇总。图8 表明，随长径比增加，相同 y/ε ε对应的 0/w wΔ 值一般相应增大。在图8(a)中，拉-压相等循环加载试件的轴向变形ε′仅在最后几级加载过程中使跨中侧向位移有少量增加，其他多数时刻ε′均使跨中侧向位移变小。图8(b)中，拉-压不等试件随长径比增加，轴向压缩变形的贡献减小、轴向拉伸变形的贡献增大，y/ε ε较大时ε′对加大跨中侧向位移的贡献明显增大。

图7 屈曲钢筋的 ε /ε y- Δw /w0和 ε /ε y- wG - A /w0关系 Fig.7 Relationship of ε /ε y- Δw /w0 and ε /ε y - wG - A /w0 of buckled steel bars

图8 典型钢筋试件的 y/ε ε - 0/w wΔ 关系 Fig.8 y/ε ε - 0/w wΔ relationship of representative specimens

综合图7 和图8 的分析结果发现，拉-压相等试件与拉-压不等试件的屈曲变形特征存在差异。与 拉-压不等试件相比，拉-压相等试件屈曲程度较小时轴向压缩对0w减少的贡献相对更大、屈曲程度较大时轴向拉伸对0w增加的贡献相对更小。与拉-压不等试件的计算结果相比，y/ε ε较小时拉-压相等试件通过G-A 模型的几何关系基本假定计算得到的wG-A与OpenSees 计算得到的w0差距更大，ε/εy较大时wG-A与w0更接近。

由于从理论上推导GAw-与0w的关系较为复杂，本文根据上述计算结果，考虑长径比 /L d的影响，经回归分析，得到了0/w L与GA/wL- 的关系式(用于后文修正G-A 模型的GAw-)，见式(15)和式(16)，其回归效果如图9 所示，图中直线为6 种不同 /L d取值的回归公式计算结果。

拉-压相等试件：

拉-压不等试件：

图9 屈曲钢筋的 wG - A /L 与 w0 /L 关系回归结果 Fig.9 Regression result of relationship between wG - A /L and w0 /L of buckled steel bars

3.2 对G-A 模型几何关系的第二种修正方法

采用图10 所示方法也可修正屈曲钢筋的几何特征。如图10(d)所示，顶端节点竖向位移δ由两部分组成：一是由杆件轴向变形ε′引起的竖向位移δΔ ，如图10(b)所示；二是由中间节点侧向位移0w引起的竖向位移latδ，如图 10(c)所示。因此有δ=δlat+Δδ(见图10(d))。若杆件承受压(拉)力、长度缩短(伸长)，则Δδ为负(正)。因此，可根据δlat/δ和 Δδ/δ的计算结果分析屈曲钢筋顶部端节点竖向位移的组成方式。

提取有限元计算结果，并按下式计算δlat/δ和Δδ/δ，其中δ为图2(c)所示有限元模型顶端节点3 的竖向位移的数值计算结果。

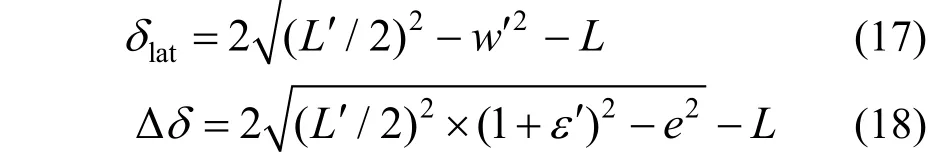
图10 顶端节点纵向位移的构成示意 Fig. 10 Composition of longitudinal displacement of top node

图11 为根据计算结果绘制的ε/εy-δlat/δ和ε/εy- Δδ/δ关系曲线。图11 表明，ε/εy较小时，顶端节点竖向位移δ主要由轴向变形ε′提供；随着屈曲程度增加、中间节点侧向位移0w增大，0w对δ的贡献逐渐增加，在中、后期甚至会引起δΔ 反向(δΔ ＜0)，这是杆件产生较大不可恢复塑性拉伸变形导致的。

图11 屈曲钢筋的 y/ε ε - lat /δ δ 和 y/ε ε - /δ δΔ 关系 Fig.11 Relationship of y/ε ε - lat /δ δ and y/ε ε - /δ δΔ of buckled steel bars

图12 为典型试件的ε/εy- Δδ/δ关系计算结果汇总。对拉-压相等试件而言，长径比较小(L/d＜8)的试件，杆件轴向变形ε′对δ的贡献随ε/εy增加而减小、Δw的贡献则逐渐增大；中等长径比(8＜ /L d＜11)试件，ε′对δ的贡献随 y/ε ε增加而增大；较大长径比( /L d＞11)试件，ε′主要为拉长，对δ的影响随 y/ε ε加大而增加。与拉-压相等试件相比，拉-压不等试件经历的拉应变相对更大，故同一循环受拉、受压产生的轴向变形的差值更大，因此在图12(b)中，ε′更快地从压缩转变为拉长，且其对δ的贡献也更大。

图12 典型钢筋试件的 y/ε ε - /δ δΔ 关系 Fig.12 y/ε ε - /δ δΔ relationship of representative specimens

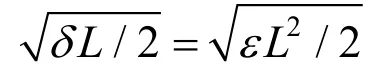
拉-压相等试件： 拉-压不等试件：

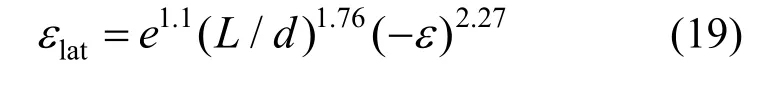
图13 屈曲钢筋的 latε 与ε 关系回归结果 Fig.13 Regression result of relationship between latε and ε of buckled steel bars

4 原始G-A 模型 pM 基本假定的修正

采用两种方法对G-A 模型假定的屈曲钢筋中间关键截面的全截面塑性弯矩 pM进行修正。

4.1 对G-A 模型 pM 假定的第一种修正方法

G-A 模型按全截面塑性假定进行计算，对于给定直径和屈服强度的钢筋来说，pM为一定值。

图14 是两个钢筋试件 (直径20 mm、 长度100 mm)的ε/εy-Mp/M0散点图计算结果，其中M0是按图2(c)所示有限元模型计算所得的屈曲钢筋跨中截面弯矩，pM则按G-A 模型给出的式(5)进行计算。图14 表明，单根钢筋循环加载时钢筋截面是逐渐进入塑性状态的，其截面弯矩在加载过程中不断变化，且在屈曲程度不严重(应变比ε/εy小于4～6)时，Mp远大于M0(约为2 倍～6 倍)，可见Mp会导致明显误差，这与文献[17]的理论分析结果是一致的，因此有必要对Mp进行修正。

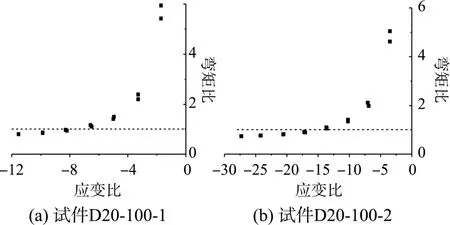
图14 钢筋试件的 y/ε ε - p 0/M M 散点图 Fig.14 y/ε ε - p 0/M M scatter plot of specimens

根据各钢筋试件的 y/ε ε-0p/M M计算结果，考虑应变比和长径比影响，经回归分析，可得到式(21)和式 (22)的修正方法，其散点图和回归效果如 图15 所示，图中曲线为5 种不同 /L d取值的回归 公式计算结果。

图15 典型钢筋试件最大压应变处的 y/ε ε - 0 p/M M 关系 Fig.15 y/ε ε - 0 p/M M relationship at maximum compression strain of representative specimens

4.2 对G-A 模型 pM 假定的第二种修正方法

第二种方法仍沿用全截面塑性假定，但考虑轴力影响、中性轴位置的变化，经理论推导和回归分析得到中间截面的弯矩修正系数。

G-A 模型按式(10)计算塑性弯矩 pM′时可考虑轴力的影响，其中θ取值与中性轴位置有关，故本文首先根据有限元计算结果对中性轴位置进行分析。图16 是屈曲钢筋在各级加载循环下最大压应变处中间截面的应力分布规律(图中实线)，为方便回归计算，可采用图中虚线所示的简化应力分布进行分析，可见中性轴位置并非如G-A 模型假定是固定的，随着屈曲程度加重(或 y/ε ε加大)中性轴逐渐向y轴正向移动。

图16 钢筋试件最大压应变处截面应力分布及简化 Fig.16 Stress distribution and idealization along cross section at maximum compression strain of specimens

采用参数naxx定义中性轴位置，naxx等于中性轴距离钢筋截面圆心的长度，统计分析发现naxx主要与 y/ε ε和长径比L/D有关，经回归分析，可得

如下中性轴位置naxx的计算式(式中r为钢筋半径)。 拉-压相等试件：

拉-压不等试件：

将式(10)改写为参数naxx的形式，则考虑轴力影响的 pM′修正表达式为：

将式(23)和式(24)代入式(26)，可得：

拉-压相等试件：

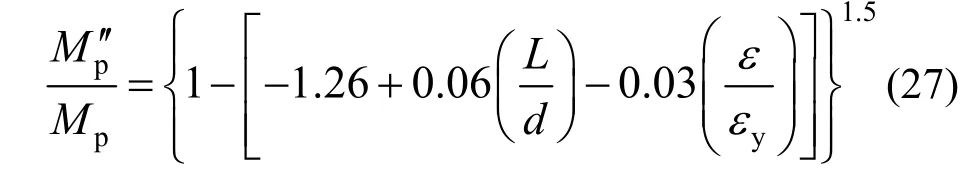
拉-压不等试件：

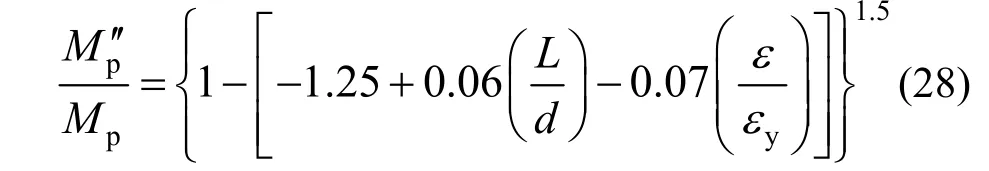
由于考虑轴力影响的全截面塑性应力分布与试件跨中截面的实际应力分布形式(见图16)仍存在一定差距(与各钢筋纤维屈服后强化程度不同有关)，为提高精度，本文引入修正系数α=M0/Mp′ ，并根据各钢筋试件的有限元计算结果回归得到了α的计算表达式：

因此，同时考虑中性轴位置变化、截面应力分布特征的弯矩修正系数为ΩM2=α(Mp′ /Mp)。

5 G-A 模型σ-ε 关系式的修正

基于前文所述的方法，可对G-A 模型的几何关系和跨中全截面塑性假定进行修正。

1) 几何关系修正

a) 跨中侧向位移GAw-的修正系数 wΩ

修正系数Ωw=w0/wG-A，将式(15)和式(16)分别代入 wΩ的定义式，可得：

拉-压相等试件：

拉-压不等试件：

b) 顶端竖向平均应变GAε-的修正系数 εΩ

修正系数Ωε=εlat/ε，式中ε为按G-A 模型计算的平均应变，将式(19)和式(20)分别代入 εΩ的定义式，可得：

拉-压相等试件：

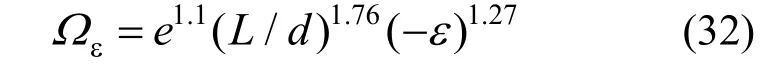
拉-压不等试件：

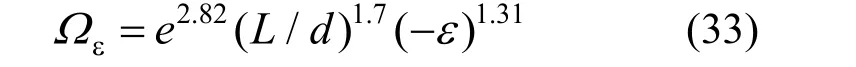
2) 跨中截面弯矩 pM的修正

a)pM的第一种修正方法(M1Ω)

弯矩Mp的修正系数ΩM1=M0/Mp，根据式(21)和式(22)以及 M1Ω的定义式，可得：

拉-压相等试件：

拉-压不等试件：

b)pM的第二种修正方法(M2Ω )

弯矩Mp的修正系数ΩM2=αMp′ /Mp，根据 式(27)～式(29)以及 M2Ω的定义式，可得：

拉-压相等试件：

拉-压不等试件：

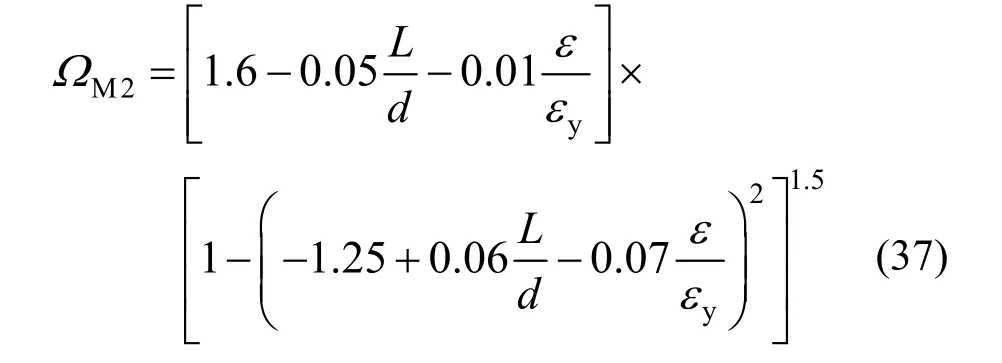
在同一坐标系下计算并绘制由上述4 个修正系数(Ω i,i=1, 2, 3, 4)得到的-ε曲线，并与G-A 模型、OpenSees 模拟结果、以及根据试验数据得到的σ-ε曲线进行比较，可对比、判断四种修正系数的效果。图17 以拉-压相等循环加载的钢筋试件18-150-1、拉压不等试件18-150-2 为例给出了计算结果的对比，图中虚线为试验所得屈曲钢筋的σ-ε滞回曲线，粗黑点为各级加载循环下与最大压应变对应的平均应力试验结果。

图17 各方法修正的平均应力-平均应变骨架线对比 Fig.17 Comparison of average stress-strain skeleton curves modified by different methods

因此，对于原始G-A 模型的σ-ε关系(式(12))，本文建议采用如下方法进行修正：

拉-压相等试件：

拉-压不等试件：

式中：εΩ按式(32)、式(33)计算；M1Ω按式(34)、式(35)进行计算。

6 修正G-A 模型的程序实现及校核

如前所述，Kunnath 等[16]以及文献[17－18]建议的修正方法并未考虑G-A 模型的理论误差，其修正方法是基于现象学而提出，引入的参数缺乏受力机理分析。本文基于屈曲钢筋的变形规律、受力特征提出了修正G-A 模型。

6.1 修正G-A 模型的程序实现

在OpenSees 平台上，定义新的单轴材料模型Modified G-A Steel Material，通过编制相应的子程序将修正G-A 模型在OpenSees 中予以实现。

OpenSees 的单轴材料模型Reinforcing Steel Material 可考虑屈曲效应[15]，其采用的是Kunnath 等建议的基于原始G-A 模型的修正屈曲模型[16]。文献[17]为方便使用将Reinforcing Steel Material 模型的三个外部输入参数(β、r和γ)简化为一个参数。经试算后本文发现，对于一些试件，这种方法计算得到的平均应力在第三、四象限(反向受压的加载过程)退化过于严重，故本文在编制修正G-A 模型的子程序时除采用参数β用于调整屈曲骨架线与未屈曲σ-ε骨架线的交点位置外，还保留了参数r，将其用于调节屈曲骨架线与未屈曲骨架线之间的位置。

6.2 修正G-A 模型的校核

在OpenSees 平台上，分别采用文献[17]的屈曲钢筋循环拉压试验、Monti 等的试验[7]得到的σ-ε曲线试验结果(详见图18～图19 中的虚线)，对本文建议的修正G-A 模型进行了校核。

建立有限元模型时，屈曲钢筋采用桁架单元(Truss)单元模拟，截面划分时将钢筋定义为单根纤维(Fiber)，钢筋纤维则分别采用三种单轴材料模型进行定义，即原始G-A 模型、Reinforcing Steel Material 模型(后文图中表示为“RSM 模型模拟”)以及Modified G-A Steel Material(即修正G-A模型)，各单轴材料模型除了考虑屈曲效应外，还采用相同的方法和参数取值考虑了低周疲劳效应。

图18 基于文献[17]屈曲钢筋试验结果的σ-ε曲线模拟结果对比 Fig.18 Comparison of computational σ-ε curves based on experiments of buckled steel bars in reference [17]

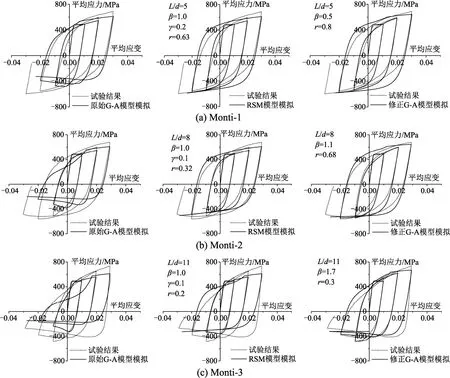
图19 基于文献[7]屈曲钢筋试验结果的σ-ε曲线模拟结果对比 Fig.19 Comparison of computational σ-ε curves based on experiments of buckled steel bars in reference [7]

图18～图19为部分不同长径比钢筋试件的有限元计算结果与试验结果对比。文献[17]的相关材料参数取值见前文。对于Monti 等的试验[7]，根据文献[7]给出的相关材料参数取值，有限元计算时Esh=0.04Es，εsh=0.01。由于Monti 等的试验[7]缺乏部分确定低周疲劳模型的相关参数(如钢筋直径)， 其有限元分析暂忽略疲劳效应的影响，这导致有限元模拟结果的误差有所增大。Reinforcing Steel Material 模型的源程序中参数β在被固定为1.0，用户无法调节屈曲开始点的位置，且参数r和γ对卸载及反向受拉段的平均应力-平均应变曲线的调整相互影响，故图18～图19 的RSM 模型计算结果均是经过反复试算后所得到的最优结果。

图18 与图19 的对比结果表明，原始G-A 模型的模拟结果较差，特别是 /L d较小的试件，在第三、四象限模拟结果与试验结果差别较大；Reinforcing Steel Material 模型的模拟效果相对于G-A 模型有明显改善，但仍存在不可忽视的误差；修正G-A 模型不仅在每级循环最大压应变处模拟结果更准确，而且从最大拉、压应变处卸载后反向再加载曲线也与试验结果更吻合，显然其模拟效果优于前述两个模型。

分析结果表明，修正G-A 模型效果最优，但与试验结果相比仍存在误差，这与修正G-A 模型采用图5 所示简化三塑性铰力学模型等有关，有待研究更合理的屈曲模型对其进行改进。应用分析时，对L/d较小的钢筋，建议采用修正G-A 模型；L/d较大时，若不需考察RC 试件受力后期的承载力退化规律，可采用更简化的原始G-A 模型进行计算。

7 结论

基于有限元分析结果，对G-A 模型的几何关系和截面弯矩进行修正，建立了屈曲钢筋的修正材料模型。

(1) 有限元分析结果表明，屈曲钢筋的跨中截面应力分布与G-A 模型采用的全截面塑性基本假定差别较大。循环加载初期、应变比较小时截面弯矩远小于全截面塑性弯矩 pM；加载后期部分纤维进入强化，且中性轴向受压侧移动，其截面弯矩大于 pM。

(2) 可采用两种方法修正G-A 模型采用的全截面塑性基本假定：① 基于弯矩比-应变比有限元计算结果，经回归分析得到弯矩修正系数；② 沿用全截面塑性弯矩，但考虑中性轴位置变化、轴力影响等得到弯矩修正系数。

(3) G-A 模型的几何关系忽略了轴向变形影响，导致屈曲钢筋跨中侧向位移计算结果存在明显误差。

(4) 可采用两种方法修正G-A 模型的几何关系：① 将屈曲钢筋的中间节点侧向位移分解为由顶端竖向位移引起的侧移和由轴向变形引起的侧移；② 将顶端竖向位移分解为由中间节点侧向位移引起的变形、由轴向变形引起的变形两部分。

(5) 多组屈曲钢筋试验的校核分析结果表明，修正G-A 模型的计算结果明显优于原始G-A 模型。