深地能源工程热水力多场耦合效应高效模拟方法

赵志宏，刘桂宏，徐浩然

(清华大学土木工程系，北京 100084)

当今世界面临的土地短缺、环境污染和能源枯竭等问题，使得深部地下空间开发利用已成必然趋势[1―2]，如水电工程引水隧道最大埋深突破2400 m，南水北调输水隧道最大埋深1150 m，高放废物地质处置库埋深500 m～1000 m，地热、矿产、油气资源开采深度已达3000 m～8000 m(图1)。深地能源工程旨在将地球深部蕴藏的能源提取出来或将人类生产生活产生的废物永久封存于地球深部，都涉及到储层岩体复杂的热(T)-水(H)-力(M)-化(C)多场耦合效应及其动态调控。深部岩体在高地应力、高地温、高渗透压等极端条件的耦合作用下，不仅岩体本身的物理力学性状较浅部发生了显著改变，而且多物理、化学场的耦合效应更为明显。深地能源工程导致地震、地下水位下降等灾害事故频发，通常难以有效预测与防治，故全面深入理解深部岩体的多场耦合效应是深地能源工程成功建设和安全运行的重要理论基础。

图1 典型深地能源工程示意图 Fig.1 Schematic diagram for the typical deep geo-energy projects

由于深地能源工程的隐蔽性，仅通过室内试验和现场实测很难完全掌握储层岩体复杂的耦合机理及其长期耦合效应，主要存在的技术困难有：如何准确获取深部岩体的物理力学参数；如何准确施加反映深部岩体赋存环境的边界条件与初始条件；如何实现试验数据的实时监测与动态传输。准确高效的数值模拟则可以克服试验研究遇到的上述难题，是研究深地能源工程多场耦合效应的另一重要手段。自20 世纪80 年代初，国内外学者已开始关注深部岩体多场耦合效应，尤其在DECOVALEX (development of coupled models and their validation against experiments)[3]、 GTO-CCS (geothermal technology office’s code comparison study)[4]等国际合作项目的推动下，多孔介质多场耦合作用的理论框架与模拟算法已日臻成熟，已可满足近场模拟的需求。但是，对于远场尺度且考虑围岩-结构相互作用的数值模拟，在精度和效率方面尚需提高。

已在深地能源工程多场耦合效应评价中广泛应用的数值模拟方法主要包括有限元、边界元、有限差分、有限体积等，主要的代表性多场耦合模拟程序如表1 所示[5―6]，其中，多数程序都可进行渗流传热过程的耦合分析，在此基础上部分程序可进行热-水-力三场、甚至热-水-力-化四场的耦合模拟。Rutqvist[21]采用TOUGH-FLAC 研究了阿尔及利亚InSalah CO2地质封存、美国Geysers 地热田等深地项目中的岩体变形与压力变化规律。朱万成等[22]提出了岩体损伤过程中的热-水-力多场耦合模型，并在COMSOL平台实现了耦合方程的有限元求解。Kong 等[23]基于OpenGeoSys 建立了热储井间距优化方法。THYME3D[24]、ROLG 等[25]程序考虑了液气转换与蒸气传输。Pan 等[26]将细胞自动机的思想引入到岩石力学中，利用简单的弱化元胞单元来模拟复杂裂隙网络模型的力学行为，并应用到热-水-力耦合模拟中。可见，基于连续介质力学的深部岩体多场耦合模拟方法发展很快。

表1 深地能源工程多场耦合程序[5―6] Table 1 The codes for modeling the coupled processes in deep geo-energy engineering[5―6]

多数深地能源工程都用到钻井进行能量或物质的转移，但常规井筒结构(直径约0.1 m～0.2 m)与储层本身(＞100 km2)存在3 个到4 个数量级以上的尺度差异，导致大尺度数值模型中精细刻画井筒结构的计算难度很大。Al-Khoury等[27―28]和Saeid等[29]将三维井筒结构简化为一维线单元模型，显著提高了深地工程数值模拟的效率。

本文基于三维井筒结构一维线单元假设，提出一种适合于深地能源工程远场尺度的热-水-力多场耦合效应高效模拟方法，并依托我国京津冀及周边地区典型水热型地热田群井系统开展案例研究，揭示深部热储温度场、渗流场、变形场的长期演化 特征。

1 模拟方法

深地能源工程包含若干储层与盖层，以及大量开采井和回灌井，其典型井筒结构如图2 所示，通常采用多开成井模式，包括泵室段、井壁段、滤水段等，井段数量根据井深与储层性质设计。盖层以上部分放入套管，并采用水泥砂浆完井。储层部分放入滤水管，提供流体交换通道。

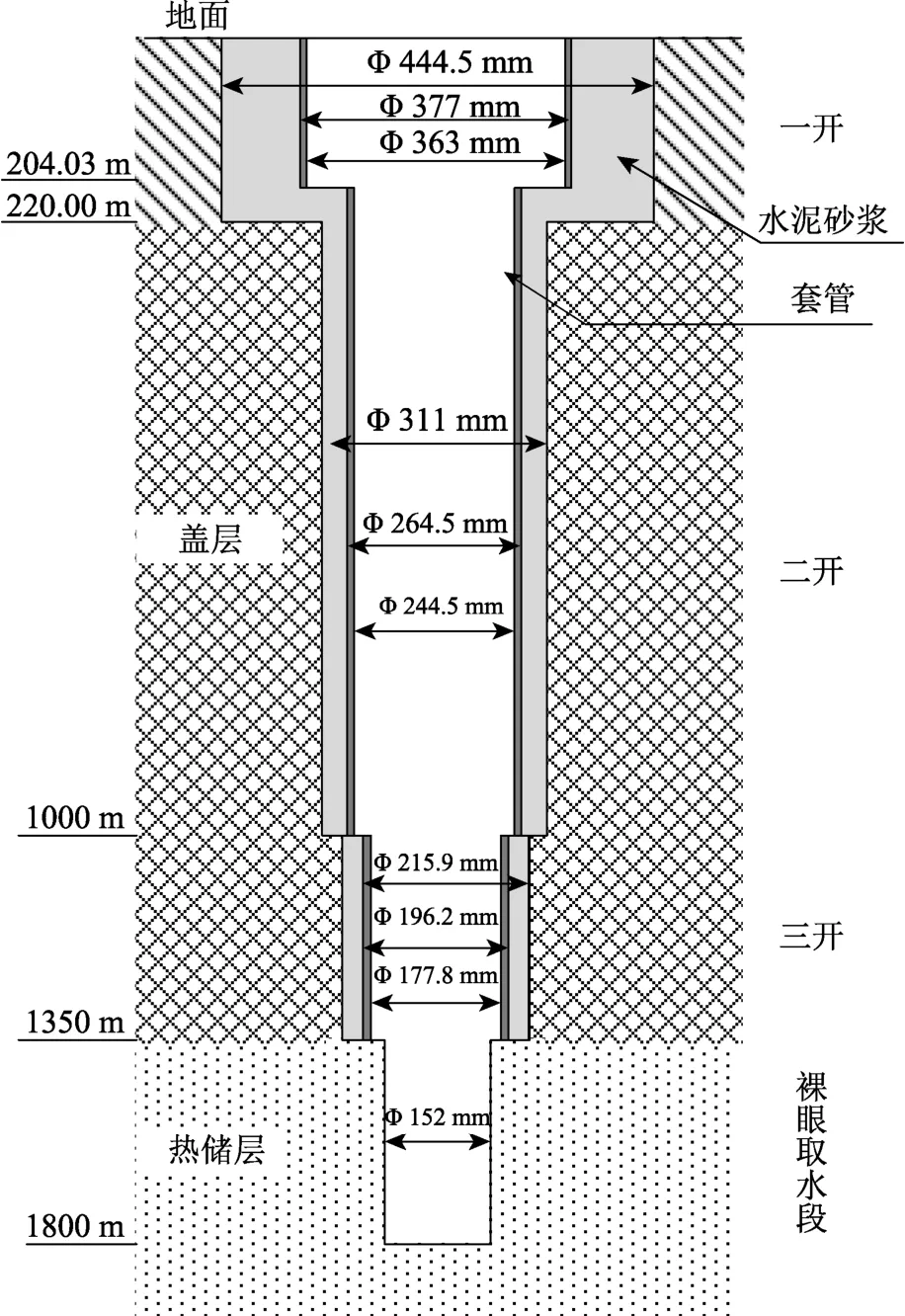
图2 深地能源工程典型井筒结构 Fig.2 Schematic diagram of a typical well completion in deep geo-energy engineering

本节引入一维线单元对该三维井筒结构进行简化，考虑沿井筒轴向的渗流传热过程，井筒内流体与盖层的热交换通过等效换热系数来近似考虑，其它主要假设条件包括：

1) 储层处于完全饱和状态，且不考虑储层内气液相变过程；

2) 盖层处于完全干燥状态，且不考虑不同储层之间的水力联系；

3) 井筒内流体沿轴向流动，且同一深度流速沿径向处处相等；

4) 考虑井筒内流体性质如密度、粘度、热传导系数、热容等与温度的相关性，但不考虑井筒内气液相变过程。

1.1 储层

储层中渗流过程可用质量守恒方程描述：

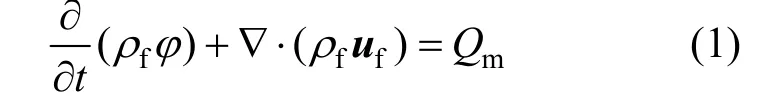
式中：t/s 为时间；fρ/(kg·m-3)为流体密度；φ为孔隙率；Qm/(kg·m-3·s-1)为流体质量源项；达西流速uf为：

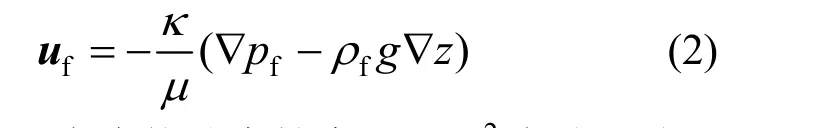
式中：μ/(Pa·s)为流体动力粘度；κ/m2为储层渗透率；pf/Pa 为流体压力；g/(m·s-2)为重力加速度；z/m为竖向坐标，向上为正。

根据多孔介质弹性理论有以下关系[30]：

式中：S/Pa-1为储水系数，可表示为孔隙率φ、Biot系数Bα、流体体积模量Kf和储层岩体体积模量Kd的函数：

联立式(1)～式(3)可得：

储层中热对流-传导过程可用能量守恒方程描述：

式中：Cp,f/(J·kg-1·K-1)为恒压下流体的比热容；T/K为温度；Q/(W·m-3)为热源； (ρCp)eff/(J·kg-1·K-1)为储层岩体等效体积热容，可表示为：

式中，effk/(W·m-1·K-1)为储层岩体有效导热系数，是储层导热系数sk和流体导热系数fk的加权平均值：

多孔介质弹性理论可用于描述热储中流体、温度、变形之间的相互作用关系，即应力张量σ、应变张量ε、热应变Tε与孔隙水压力fp的关系为[30]：

式中，C/(N/m)为储层岩体刚度张量，应在排水且恒定孔压条件下测量应力引起的应变。

温度应变可以表示为：

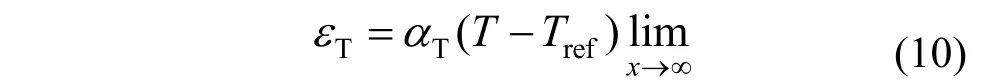
式中：Tα为储层岩体热膨胀系数；refT/K 为储层初始温度。

根据Biot 定理，流体孔隙压力与多孔基质的膨胀和流体含量有如下关系：

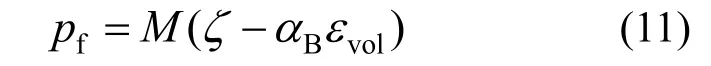
式中，M/Pa 表示Biot 模量，是储水系数S的倒数。 在纯重力荷载下，处于平衡状态的储层可用Navier 方程来表示：

式中，ρav=ρfφ+ (1 -φ)ρs/(kg·m-3)为储层岩体等效密度。

1.2 盖层

对于盖层，其传热过程只考虑热传导：

1.3 断层

储层中常含有断层等不连续体，其渗流过程可用质量守恒方程描述：

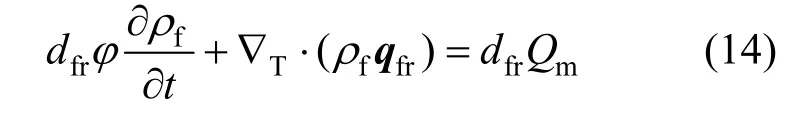
式中：dfr/m 为断层开度；qfr为断层中的体积流量，可表示为：

断层中热对流-传导过程可用能量守恒方程来描述：

1.4 一维井筒简化模型

一维井筒单元中不可压缩流体的能量守恒方程为[31]：

式中：Aw/m2为地热井的截面积；/(m/s)为沿井筒轴向的平均流速；Qw为通过地热井壁发生流体与外部围岩的热交换；fD为达西摩擦因子，与雷诺数(Re)、表面粗糙度e、地热井径di有关：

对于层流(Re＜2000)，Df与井筒的表面粗糙度e无关，可用Stokes 公式计算：

对于湍流(Re＞2000)，Df可用Haaland 公式计算[32]： 定义等效传热系数(hZ)eq来近似描述地热井内流体与周围岩石之间的传热过程：

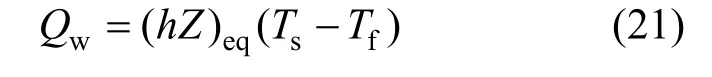
式中：Tf/K 为地热井中流体的温度；Ts/K 为岩石温度。考虑单位长度内从流体通过井筒的热流相等，可推导出等效传热系数为：

式中：r0/m、r1/m 和r2/m 分别为套管内径、外径和水泥砂浆外径；kp/(W·m-1·K-1)和kc/(W·m-1·K-1)分别为套管和水泥砂浆的导热系数。

流体井筒内产生的热膜阻hint可通过下式计算：

式中：Nu为努塞尔数。对于层流时，Nu为常数3.66。对于湍流(3000＜Re＜6×106，0.5＜Pr＜2000)，努塞尔数可由下式确定：

式中，Pr表示普朗特数。

1.5 初始条件与边界条件

储层初始水压按静水压力考虑，Dirichlet 或Neumann 边界条件均可应用于模型顶部、侧面和底部边界。井筒内初始水压也按静水压力考虑，运行开始后(t＞ 0)，井口设为流速边界条件。

模型初始温度场可根据地温梯度TΔ 确定：

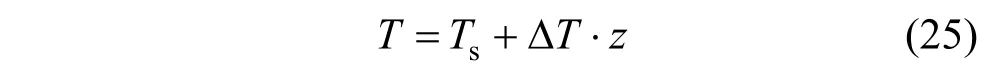
式中：Ts/K 为地面温度。Dirichlet 或Neumann 边界条件均可应用于热储模型顶部、侧面和底部边界。井同内初始温度等于围岩初始温度，运行开始后(t＞ 0)，回灌井口温度固定为：

开采井井口的热通量设为：

在井筒与储层围岩界面，将质量通量(Mt)应用于储层内边界：

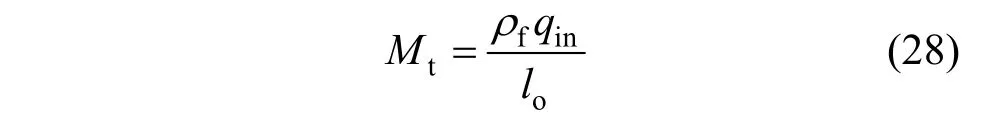
式中，lo/m 为地热井的裸眼段长度。

根据回灌井井底温度(Tb)，在储层内边界设置线热源：

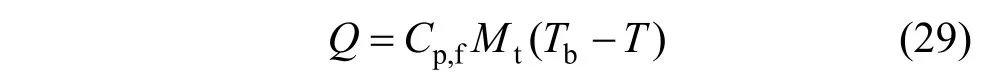
开采井井底温度取为储层内边界温度均值[29]：

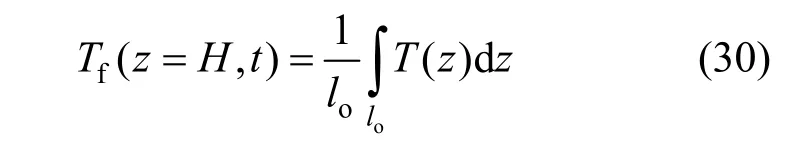
模型顶部为自由边界，底面设为固定位移边界。模型侧边水平位移为0，只允许竖向位移。

1.6 流体参数

深部储层中流体密度、粘度、导热系数和比热容随温度变化按如下经验公式考虑[33―34]：

1.7 模型求解过程

基于有限元计算平台COMSOL，建立远场尺度深地能源工程三维数值模型，采用四面体单元离散数值模型，一维线单元代表井筒。对于储层岩体中的热-水-力耦合控制方程(式(5)、式(6)、式(12))、盖层岩体中传热控制方程(式(13))、井筒中渗流传热控制方程(式(16)和式(21))，采用COMSOL 中的并行直接稀疏求解器接口求解非线性系统，模型求解流程如图3 所示。

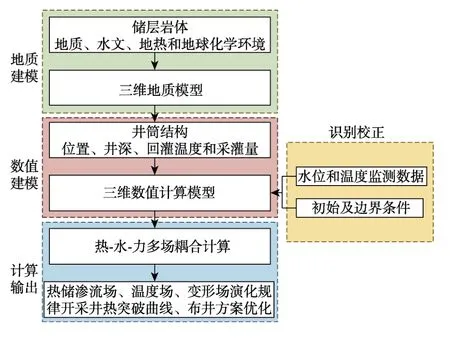
图3 计算流程示意图 Fig.3 Calculation procedure for the reservoir-well model

2 案例研究

2.1 北京东南城区地热田

2.1.1 地热地质条件

北京东南城区地热田位于天安门广场以东至东四环附近(图4)，属典型坳陷盆地，热储层包括蓟县系铁岭组(埋深约578 m～1200 m)和雾迷山组(埋深约517 m～2456 m)，均为水热型热储，岩性为白云岩。由于长期地质构造作用，上述两热储层由洪水庄组页岩隔开，铁岭组热储由下马岭组页岩覆盖，受崇文门—胡家沟大断裂带的影响，地热田中部及偏北方向铁岭组缺失(图5)。

图4 地热井分布及剖面I-I’位置示意图 Fig.4 Locations of geothermal wells and geologic section I-I’

20 世纪70 年代北京东南城区地热田开采以区域供暖为主，之后随着开采井数量的增加，地热水开采量急剧增加，导致热储压力迅速下降(水位下降0.83 m/a～2.36 m/a)，严重威胁地热资源的可持续开采。自2000 年以来，通过地热尾水回灌部分实现了地热资源的可持续开采。

2.1.2 模型建立与校正

数值模型尺寸为长11.6 km，宽8.5 km，高2 km，共包含2 个热储层、9 个不同地层、4 条断层以及39 口地热井(其中8 口回灌井)(图6)。兼顾计算精度与效率，地热井与断层周边区域网格约尺寸约为2.5 m，而远离地热井或断层的区域则使用较大尺寸的网格，约为 430 m。模型总计包含662817 个四面体单元，39 口地热井由1291 个一维线单元代表(图6)。

图5 I-I’剖面示意图 Fig.5 Geologic section I-I′ of geothermal field

图6 北京东南城区地热田数值模型 Fig.6 Numerical model of the Beijing City geothermal field

模型内包含4 口水位监测井，即井2、井3、 井5 和井7，监测历时11 年(1971 年―1981 年)，开采井流量与监测井水位变化如图7 所示[35]。通过对水位监测数据的拟合来反演热储渗透率及标定模型边界水位，所求得的热储渗透率及其余输入参数如表2 所示。计算结果表明，4 口监测井的模拟水位与实测水位基本吻合，可在此基础上模拟两个热储对回灌的响应以及预测地热井在未来50 年使用寿命内的热突破。此外，由于铁岭组热储的厚度小于雾迷山组热储(雾迷山组未揭穿)且整体水位在1971 年更低，随着开采井数量及开采量的增加，经过11 年的开采，到了1981 年，铁岭组热储出现了大范围的抽水漏斗(图8)。

东南城区地热田温度约为90 ℃，而回灌水温度为30 ℃，故应按式(31)～式(34)考虑流体性质(密度、粘度、导热系数和比热容)随温度的变化。Yang 等[35]提供了地温梯度分布(图9)，结合模型输入参数(表2)，计算得到模型的初始温度场分布如图10 所示。

2.1.3 计算结果分析

图7 北京东南城区地热田数值模型水位校正 Fig.7 Calibration of water level for numerical model of the Beijing City geothermal field

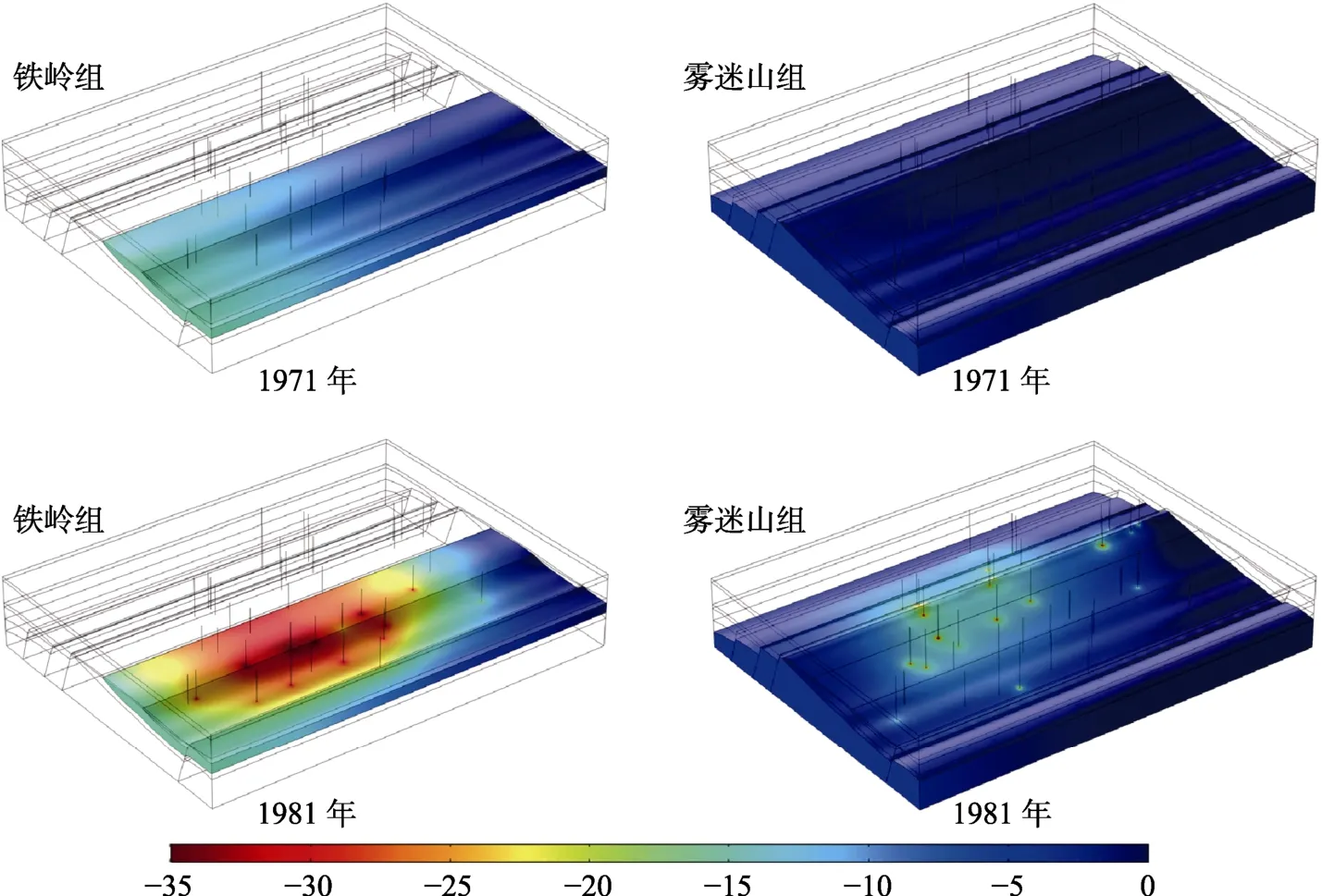
图8 北京东南城区地热田数值模型水位分布图 /m Fig.8 Distribution of water level in the numerical model of the Beijing City geothermal field

本文考虑两种工况：一种为开采率和回灌率相等，即地热田注采比为0.26；另一种工况回灌率为 开采率的2.875 倍，即地热田注采比为1.0。通过对比分析这两种模拟工况，揭示注采比对热储长期性能的影响。注采比为1.0 是地热资源可持续开发的趋势，但我国实际地热开采中注采比仍远小于1.0。该地热田回灌井位置分布不均匀，选择两个包含采灌井的典型区域来解释模拟结果(图4中虚线方框)。在模拟过程中对开采温度进行监测，并将开采温度降低1 ℃的时间定义为开采井的热突破时间。两种工况在普通台式计算机(CPU i7-4790K，内存16 GB)上都需要约9.5 h 的计算时间，这对于地热项目的设计和管理是合理的。

表2 模型拟合及输入参数列表[36―38] Table 2 Fitting and input parameters for the numerical model[36―38]

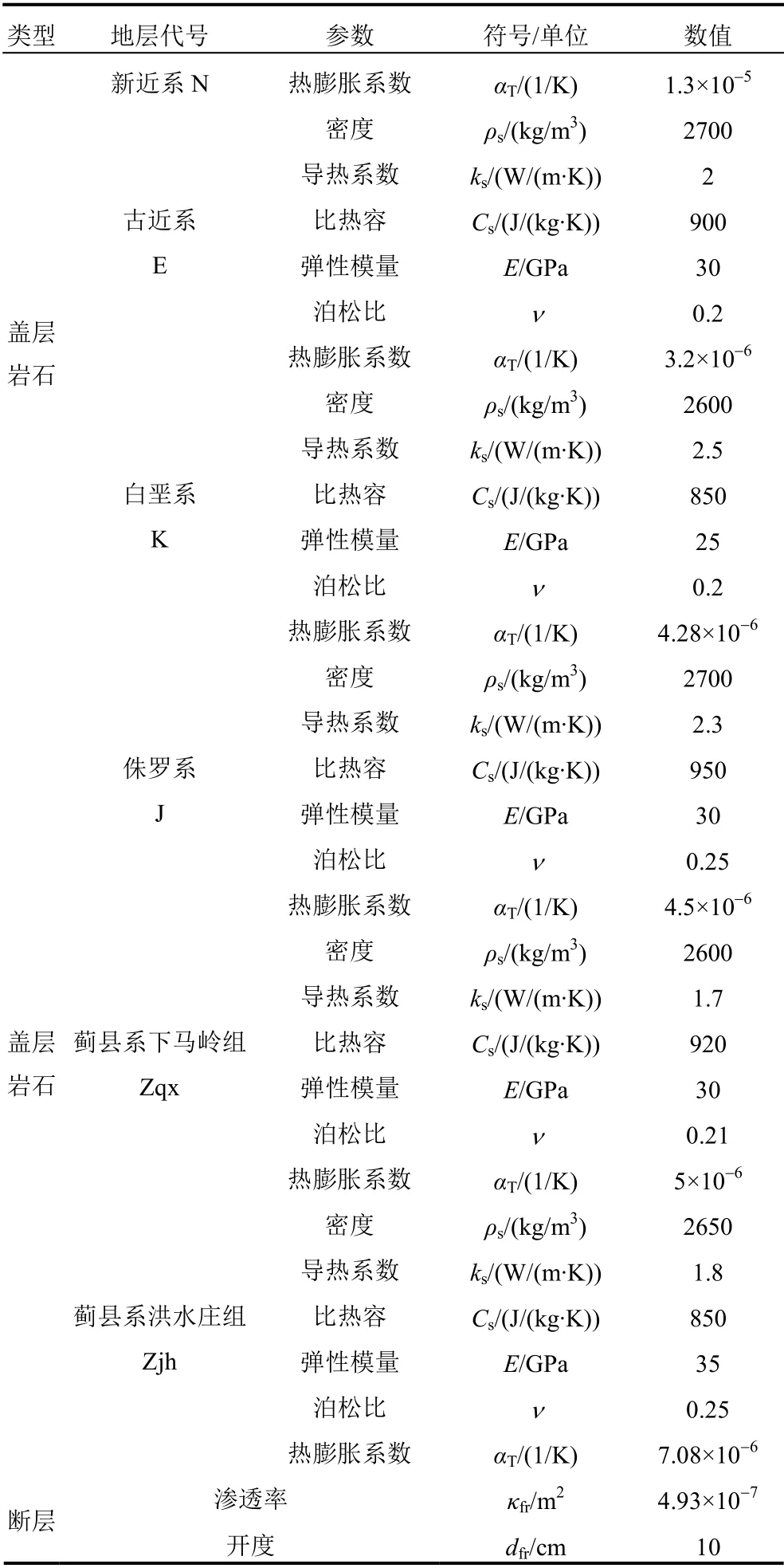
(续表)

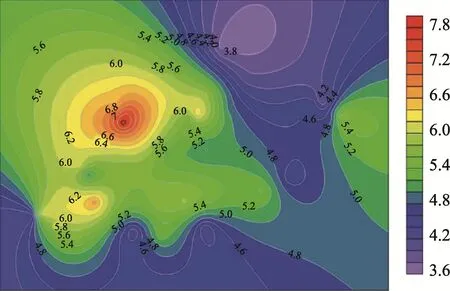
图9 北京东南城区地热田数值模型地温 梯度分布 /(℃/100 m) Fig.9 Distribution of temperature gradient in the numerical model of the Beijing City geothermal field

图10 北京东南城区地热田数值模型初始 温度场分布 /(℃) Figure 10 Initial temperature field in the numerical model of the Beijing City geothermal field

1) 工况I：注采比0.26

图11 给出两个热储温度场随时间的演变过程。随着开采时间的延长，冷锋面由回灌井向开采区移动，部分靠近回灌井的开采井发生了热突破(图12)，对于雾迷山组热储，由于井29 和井35 距离回灌井R2 只有240 m 和460 m，因此井29 在8.8 a 就发生了热突破，井35 在22.5 a 发生了热突破。对于铁岭组热储，井31 和井R3 形成地热对井系统，井31在23.3 a 发生热突破，而回灌井井G 的冷锋面在 50 a 内尚未到达井32、井15、井9 和井27。

2) 工况II：注采比1.0

与工况I 相比，由于增大了回灌量，冷锋面在工况II 中运移得更快，导致有更多的开采井发生了热突破(图12)，对于雾迷山组热储，井29、井35和井5 分别在2.1 a、8.0 a 和14.8 a 时就发生了热突破，但回灌没有影响井16 的温度变化，因为井16距离回灌井R2 和井E 约为883 m 和611 m。对于铁岭组热储，除了井27 以外的所有开采井都发生了热突破，考虑到地热系统会运行很长时间，井27在未来也有可能发生热突破。

3) 热储变形分析

从回灌井中注入冷水到高温高压的热储中，必然会导致热储在回灌压力及热应力的作用下发生变形，在长期回灌条件下，回灌井周围的热储逐渐被冷却，沉降量较大的区域均出现在回灌井周围(图13)，但这并不一定意味着回灌一开始就导致热储产生较大的变形，事实上，在回灌开始的较短时间内，热储因回灌压力的作用导致热储发生了膨胀，即产生了正向位移，并反映在地表沉降量变化中(图14)，说明在回灌初期，回灌压力对热储的变形起主导作 用。但随着回灌时间的增加，热储逐渐被冷却，这时热应力对热储的变形作用大于回灌压力的作用，并发生了“热收缩”现象，导致热储沉降量逐渐增大。对于开采井，由于开采高温地热水，导致开采井周围的岩石遇热发生了膨胀，在地表开采井周围均出现了正向位移(5 mm～12 mm)，但随着冷锋面逐渐向开采井运移，开采井井底周围岩石遇冷收缩，导致沉降量逐渐增大，如井29(图14)。

图11 北京东南城区地热田数值模型热储的温度场分布 /(℃) Fig.11 Temperature distribution in the geothermal reservoirs of the Beijing City geothermal field

图12 北京东南城区地热田数值模型典型地热井的热突破曲线及温度分布 /(℃) Fig.12 Thermal breakthrough curves of the representative production wells and temperature distribution in the geothermal reservoirs of the Beijing City geothermal field

图13 北京东南城区地热田数值模型热储位移场分布 /mm Fig.13 Displacement distribution in the geothermal reservoirs of the Beijing City geothermal field

图14 北京东南城区地热田数值模型位移变化曲线 Fig.14 The displacement curve of the geothermal reservoirs and ground surface of the Beijing City geothermal field

2.2 山东德州城区地热田

2.2.1 地热地质条件

研究区位于山东省德州市德城区，自中、新生代以来，受燕山运动和喜马拉雅运动的影响，地壳运动总的趋势是以下降为主，长期接受沉积，并沉积了巨厚的新生界地层，厚度超过3000 m，其下为中生界地层。钻孔揭露的地层分布从上往下分别为：第四系平原组(Qp)、新近系明化镇组(Nm)、新近系馆陶组(Ng)、古近系东营组(Ed)和古近系沙河街组(Es)，热储层为新近系馆陶组，区内共有地热井86 口，其中回灌井2 口，监测井4 口(图15)。

图15 德城区地热井位置分布图 Fig.15 Distribution of geothermal wells in the Decheng district

2.2.2 模型建立与校正

数值模型区域面积约为310 km2，深度2.5 km，共包含1 个热储层、5 个不同地层以及86 口地热井(图16)。兼顾计算精度与效率，地热井及周围区域的网格细化，最大单元尺寸2.5 m，热储层区域网格细化，最大单元尺寸1 km，其余盖层网格粗化，最大单元尺寸12 km。模型总计包含308163 个四面体单元，86 口地热井由2216 个一维线单元代表(图16)。

图16 德州城区地热田数值模型 Fig.16 Numerical model of the Decheng district geothermal field

研究区内共有4 口水位监测井，即DZ1 井、DZ28 井、DZ48 井和DZ53 井，监测历史20 年(1998年―2017 年)。从1998 年开始，陆续有新的地热井投入使用且开采量逐年增加(图17)，通过对水位监测数据的拟合来反演热储渗透率及标定模型边界水位(水位埋深约70 m)，所求得的热储渗透系数及其余输入参数如表3 所示。计算结果表明，4 口监测井的模拟水位与监测水位基本吻合(图18)，可在此基础上利用模型进行德城区的采灌优化设计，此外，随着开采井数量的增加，研究区内因抽水而形成的漏斗范围在逐年扩大(图19)。

研究区内有1 口温度监测井，即DZ17 井，该井为回灌井，回灌期2016 年12 月14 日―2017 年4 月30 日，回灌结束后从7 月4 日开始，每隔1 个月监测不同井深的温度变化，持续4 个月，至11月3 日结束。通过调整模型的导热系数和比热容等参数，使模拟温度与加测温度基本吻合，最终得到的模型参数如表3 所示，计算结果表明，模拟温度值与实测温度值基本一致(图20)，说明可用该模型进行后续计算。

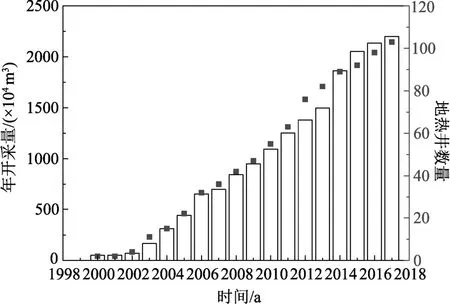
图17 德城区年开采量及地热井数量 Fig.17 Evolution of geothermal well number and production volume in Decheng district

2.2.3 计算结果分析

为控制馆陶组热储层地下水水位的持续下降和地热尾水的排放污染，地热供暖尾水必须100%回灌，以保证采灌均衡。研究区采用“一采一灌”对井模式，区内目前DZ17 井与DZ1 井组成地热对井系统，DZ31 井与DZ28 井组成地热对井系统，需给其余82 口开采井匹配相应的回灌井，在采灌量等于90 m3/h 的前提下，模拟出防止开采井热突破的最优采灌井间距，考虑到住宅小区的范围与规模，采灌井间距初步设置方案为200 m、300 m、400 m 和500 m，布井方案如图21 所示，回灌温度为30 ℃，并考虑采灌周期(4 个月开采，8 个月停采)的影响。通过计算，得到了DZ48 井、DZ53 井和DZ56 井在不同采灌井间距下的热突破曲线(图22)，随着采灌井间距的增大，开采井发生热突破的时间越长，曲线的振荡频率与采灌周期有关，振幅与井深关，开采井井深越大，温度曲线的振幅越大。将3 口监测井在不同采灌井间距下的热突破时间进行统计(表4)，当在井间距为200 m 时，3 口监测井的热突破时间均为13 a，热突破时间较短，说明采灌井间距不应小于200 m，DZ48 井在井间距小于500 m 时相比DZ53 井和DZ58 井来说，热突破时间较短，这是由于DZ48 井受到DZ54 井回灌井的影响，造成DZ48 井的热突破时间较短，由于DZ53井和DZ58 井位置比较孤立，不受周围回灌井的影 位置，避免出现“一采多灌”的情况发生，建议在实际工程中，采灌井间距应大于400 m 才能延长开采井的热突破时间。

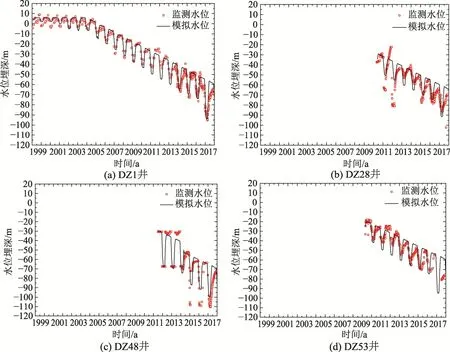
图18 德城区地热田数值模型水位校正 Fig.18 Calibration of water level for the numerical model of the Decheng district geothermal field

图19 德城区地热田数值模型不同年份的水位埋深分布云图 /m Fig.19 Distribution of water levels in the numerical model of the Decheng district geothermal field

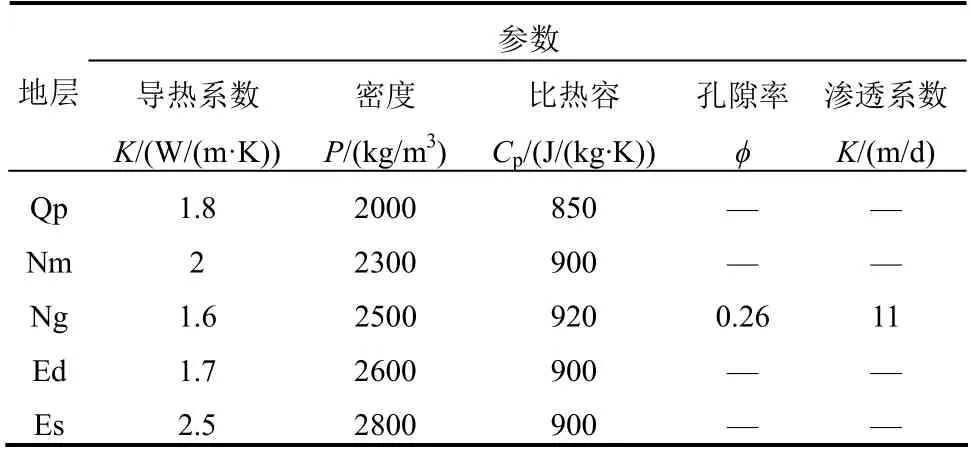
表3 德城区地热田数值模型输入参数列表 Table 3 Parameters for the numerical model of the Decheng district geothermal field

3 讨论

响，这两口监测井的热突破时间基本相同。以上结果说明，随着采灌井间距增大，能有效延长热突破时间，但同时也要考虑在集中开采区采灌井的相对

3.1 地热群井效应

在北京东南城区地热田中，对比两种模拟工况可以发现，在回灌率较大和长时间的运行条件下，更多的开采井可能受到回灌的影响(图12)，例如，回灌井G 周围的三口地热井井32、井15 和井9 组成了地热群井系统，在德州城区地热田中，DZ48井、DZ54 井及其回灌井同样组成了地热群井系统，这意味着传统的地热对井数值模型可能无法准确地预测开采井的热突破，而本文提出的深地能源工程热水力多场耦合高效数值模拟方法可为地热系统的长期管理提供一种有效考虑地热群井效应的模拟 方案。

3.2 热储之间的相互作用

北京东南城区地热田模型中包括了两个热储层，即雾迷山组和铁岭组热储层，本文重点研究了回灌井R1 和开采井30 之间的相互作用，它们彼此接近但在不同的储层中(图23)，回灌井R1 位于深层的雾迷山组热储层中，而开采井30 则位于浅层的铁岭组热储中，由于这两个热储层被洪水庄组盖层所 隔开，R1 中的回灌冷水不会影响开采井30 的温度，由于盖层不透水，冷锋面只能通过热传导在盖层中移动，在地热群井系统运行50 a 后，雾迷山组热储的回灌不会影响铁岭组热储温度。

图20 DZ17 井温度拟合曲线 Fig.20 Temperature fitting curve of the well DZ17 in the Decheng district geothermal field

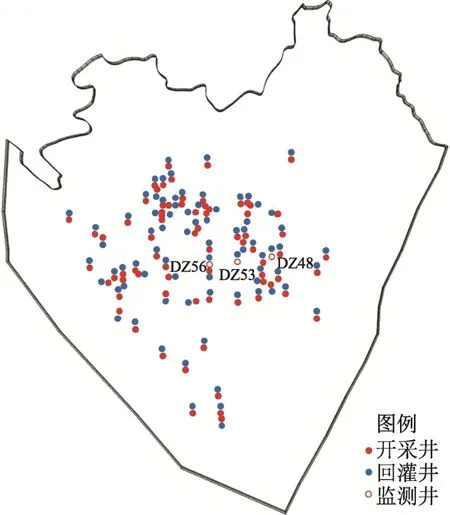
图21 德城区地热田采灌井布井方案 Fig.21 Well layout scheme for production and injection wells in the Decheng district geothermal field

图22 德城区地热田典型地热井热突破曲线 Fig.22 Thermal breakthrough curves for the representative geothermal wells in the Decheng district geothermal field

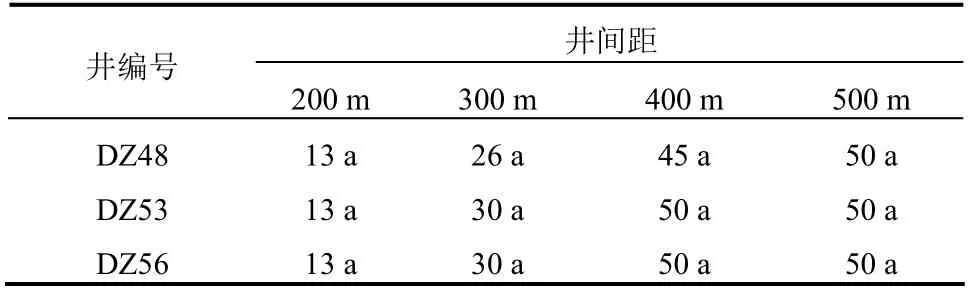
表4 德城区地热田热突破时间统计表 Table 4 Thermal breakthrough times for the geothermal wells in the Decheng district geothermal field

图23 北京东南城区地热田铁岭组和雾迷山组热储的温度分布图 /(℃) Fig.23 Distribution of temperature in Tieling and Wumishan formation geothermal reservoirs

3.3 断层的影响

北京东南城区地热田模型中还考虑了几条断层对地热群井系统运行的影响(图24～图25)，例如，回灌井T3 和T4 的深度基本相同，但井T4 穿过了 断层，回灌冷水可以快速流过断层，并使靠近断层区域的温度降低。对于穿过断层的开采井22，由于深层地热水通过断层流向井22，使得该井的开采温度随时间缓慢增加(图25)。

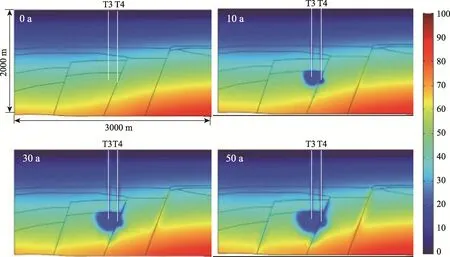
图24 北京东南城区地热田雾迷山组热储的温度分布(包括T3 和T4) /(℃) Fig.24 Temperature distribution in the Wumishan reservoir including well T3 and T4

图25 北京东南城区地热田井22 的热突破曲线 及热储温度分布 /(℃) Fig.25 Thermal breakthrough curve for the well 22 and the temperature distribution in the Beijing City geothermal field

4 结论

本文提出了深地能源工程热-水-力多场耦合高效模拟方法，并应用于北京市东南城区地热田和山东德城区地热田等深层地热开采工程，研究了地热系统的群井效应、采灌方案优化设计、以及深部热储温度场、渗流场、变形场的长期演化特征。主要结论如下：

(1) 针对深地能源工程井筒结构独特的细长型几何特点，将井筒简化为一维线单元，考虑井筒内流体沿井筒轴向的渗流传热，而井筒内流体与周围岩体的换热过程则采用等效换热系数近似考虑，套管和砂浆层的影响包含在等效换热系数中，同时，给出了描述热储热-水-力多场耦合过程的表达式，并考虑了断层的影响和流体性质随温度的变化，利用该方法实现了远场尺度深地能源工程热-水-力多场耦合效应的高效模拟。

(2) 基于北京市东南城区地热田，数值模拟结果表明，地热井的位置、深度和采灌量会对热储的长期性能产生重大影响，且不可忽略地热群井效应，应在实际工程中优化地热井布设位置以及开采量与回灌量，以避免开采井快速发生热突破。如果热储层之间有盖层隔开，则不同热储层之间并无显著影响。断层可为流体流动和热量传递提供快速通道。热储变形同时受到回灌压力和热应力的作用，这两种应力的主次作用决定了热储变形量的大小。

(3) 基于山东省德州城区地热田，根据“一采一灌”布井方案，在模型中给82 口开采井匹配了相对应的回灌井，提出了一套布井方案，并对井间距进行了敏感性分析，计算结果表明，在实际工程中，采灌井间距大于400 m 才能避免开采井发生快速热突破，且在集中开采区布置回灌井时应考虑采灌井的相对位置，避免“一采多灌”的不利情况。