底部铰支自复位钢筋混凝土剪力墙 设计与性能研究

徐龙河，张 焱，肖水晶

(北京交通大学土木建筑工程学院，北京 100044)

钢筋混凝土剪力墙侧向刚度大、承载力高、布置灵活，广泛用于高层超高层结构中。但当结构遭受较大地震时，易发生墙脚压溃、墙底出铰、墙板剪裂等破坏，导致结构残余变形明显，无法继续使用甚至引起建筑倒塌[1]。功能可恢复结构概念[2－3]提出后，国内外学者对剪力墙结构复位方式进行了讨论。

Kurama 等[4]基于预应力结构具有变形自恢复特点，首先提出无粘结预应力自复位剪力墙模型，沿墙轴向通长布置预应力筋，放张墙底与基础连接界面，通过墙体刚性转动避免墙板损伤，在预应力筋回弹和墙体自重作用下实现剪力墙复位。之后Kurama 等[5]、Holden 等[6]和Marriott 等[7]在预应力自复位剪力墙脚部增设软钢棒等耗能装置以提高墙体耗能能力。党像梁等[8]提出底部开水平缝自复位剪力墙，墙板与基础局部放张，仅在墙脚处开水平缝，并在墙内竖向布置通长的预应力筋提供复位力，有效减小开缝导致的墙体承载力下降，复位效果良好。肖水晶等[9－10]提出内置碟簧自复位剪力墙，利用碟簧使用灵活、承载力高、占用空间小等特点设计出可更换型弹性墙脚，代替传统剪力墙容易破坏的墙脚区域，实现剪力墙侧移时墙脚弹性变形并提供恢复力，复位效果良好。赵军等[11]提出高强筋材混凝土剪力墙，墙内布置钢绞线或CFRP 筋作为纵筋，通过受力纵筋弹性化的方式减小墙板残余变形，有效减小墙板破坏区域和裂缝宽度，具有一定的复位能力。目前，剪力墙实现自复位功能的途径主要有放张墙板与基础连接界面后布置预应力筋、边缘约束区底部开水平缝后布置预应力筋、用高刚度高承载力弹性装置替换易损墙脚和布置高弹性纤维复合筋等几种方式。

本文从剪力墙塑性铰区的弹性改造出发，以能实现较大弹性侧移为设计目标，将容易受损的钢筋混凝土墙底替换为能实现弹性转动的弹性墙底，提出一种底部铰支自复位钢筋混凝土剪力墙

(self-centering reinforced concrete shear wall，SC-SW)。基于ABAQUS 有限元软件对提出的底部铰支SC-SW 和普通钢筋混凝土剪力墙(SW)进行模拟，对比了相同受荷历程下两者的滞回特性。验证SC-SW 具有良好复位性能和延性，墙体损伤较低，残余变形较小，是一种可行的SC-SW 设计方式。

1 SC-SW 力学特性

1.1 SC-SW 设计概念

混凝土弹性变形范围小，耐压畏拉，压应力未达峰值已伴生塑性应变，反复加卸载作用下弹性模量下降明显。钢材弹性变形范围大，屈服强化过程中塑性应变激增。强震作用下钢筋混凝土发生的塑性应变及混凝土开裂是造成剪力墙残余变形的主要原因。观察弯曲型剪力墙破坏模式，墙体多数是由于脚部混凝土压溃，墙底塑性变形严重从而形成塑性铰，导致残余位移明显无法修复，这表明一般钢筋和混凝土的材料性能难以满足剪力墙复位功能的实现，因此对受荷过程中应力水平较高的墙底进行弹性改造，不仅可以杜绝墙板绝大部分损伤，还可以赋予剪力墙更优异的性能。本文提出的SC-SW 设计方案如图1 所示，将型钢梁与复位支撑组合构造成具有强弹性变形能力的弹性墙底，同时将上部混凝土墙板传递的内力解构。由于竖向荷载沿截面分布较均匀，合力作用点偏心小，变形过程中附加弯矩较小，竖向轴力主要由连接梁中部销轴传递，也保证了支撑更换时的竖向承载安全；水平剪力通过中部销轴传递；弯矩通过墙底两侧支撑形成的抗弯力偶传递。

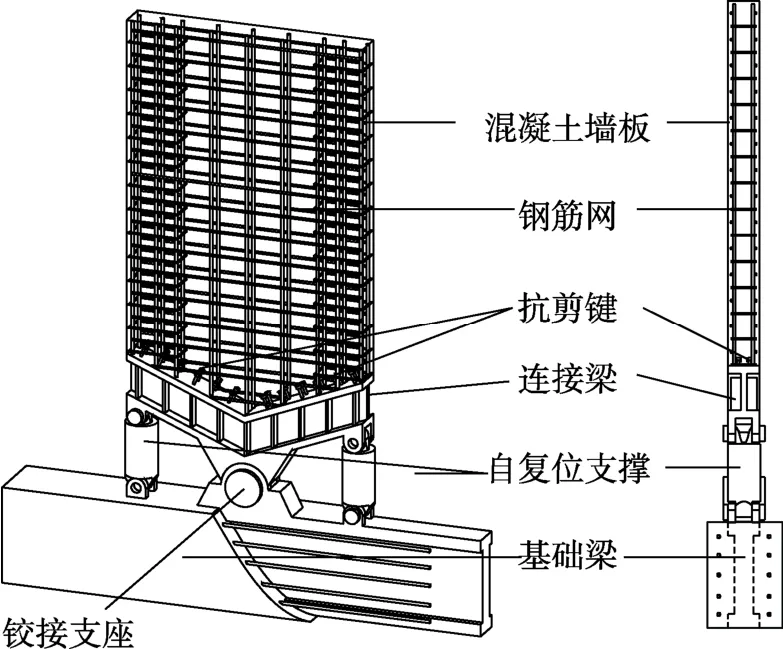
图1 SC-SW 设计方案 Fig.1 Design of SC-SW

高宽比大于2.0 的弯曲型剪力墙具有较好的抗震能力，墙体在轴向压力和地震水平力作用下，底部截面弯矩最大，墙底混凝土受力最复杂，导致剪力墙在失效过程中大部分损伤集中在墙底，轻则墙脚混凝土压溃，重则底部裂缝贯通。使用钢材构造的弯剪分离且具有弹性转动能力的墙底替换混凝土浇筑的弯剪耦合且塑性明显的墙底，这种墙底具有材料研究成熟、内力传递清晰和性能设计方便的优势，打破混凝土材料性能约束，适用于高性能剪力墙的设计。

1.2 弹性墙底力学特性

根据本文提出的设计方案，墙脚竖向位移约为1/4 墙顶侧移量，而墙脚竖向受力约为2 倍墙顶剪力值。因此，墙底配置的复位支撑要有较大刚度和较强弹性变形能力。本文采用碟簧作为复位支撑的主要受力装置。为了验证组合碟簧的受力性能，徐龙河等[12－15]对预压碟簧自复位耗能支撑进行了循环荷载试验，表明碟簧具有承载力高、无残余变形、刚度调整灵活等特点。根据墙体几何参数和性能需求确定碟簧尺寸及组合方式，以满足性能目标下的行程需求和刚度需求。将碟簧叠对合两端加挡板压缩后限制于内、外管之间，内、外管端部设置与连接梁和基础梁销轴连接的耳板。支撑不受外力时，碟簧处于压缩状态，对内、外管有一预压力，当支撑轴力小于等于该预压力时无法压缩碟簧，内外管保持静止，此时支撑刚度由内外管决定(可视为由内管和外管串联成的钢管轴向受力变形)。当支撑轴力大于该预压力时，碟簧开始被进一步压缩，支撑激活，内外管开始错动，此时支撑刚度等于碟簧组线刚度。复位支撑构造及原理如图2 所示。

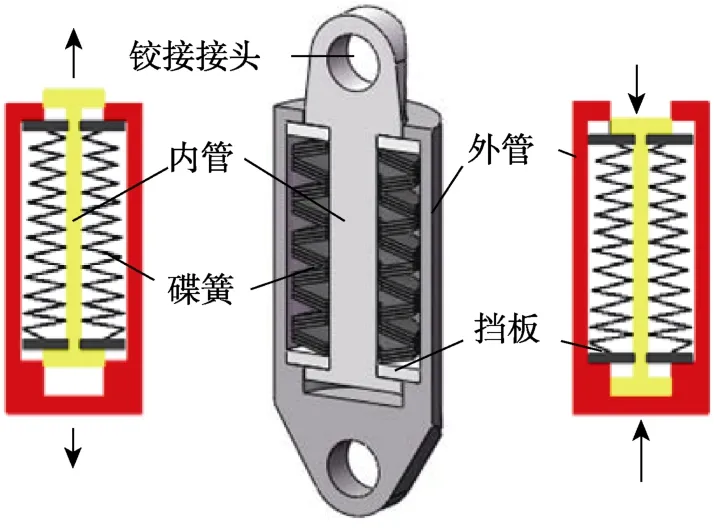
图2 复位支撑构造及原理 Fig.2 Configuration and principle of self-centering brace

利用ABAQUS 有限元软件建立复位支撑的实体模型，如图 3(a)所示。当碟簧组线刚度为20 kN/mm、碟簧预压力为400 kN、内管抗拉刚度为3.7×105kN/mm 和外管抗拉刚度为1.1×106kN/mm时，支撑在往复荷载作用下滞回曲线如图3(b)所示，可以看出，支撑初始刚度大，具有双线性滞回特性；在第一、第二刚度范围内，均能实现大位移弹性变形，验证了上述支撑弹性机制的有效性；内管、外管和挡板的变形对支撑刚度有一定的影响，例如支撑受拉时，垫板翘曲、内管拉伸和外管拉伸三种变形可以造成支撑第一刚度与第二刚度间的曲型过渡段，而支撑受压时内外管因仅端部受力，变形不明显而不会造成曲线过度段；由于内外管、碟簧组和挡板串联关系的影响，支撑第二刚度会略小于碟簧组线刚度。增大内外管和挡板的刚度会有效减小这三者变形产生的影响，因此应合理控制这三者的刚度。同时，由于支撑具有稳定简单的力学特性，不考虑内外管和垫板变形产生的影响时，为提高计算效率，可用双线性弹簧对复位支撑轴向力学性能进行简化模拟。

剪力墙弯剪作用下，墙板混凝土应力水平从两侧墙脚向截面中部和墙板上部递减，因此墙体在弯曲破坏时墙底塑性区域呈现两边高中间低的分布形状，墙底分布的裂缝也向墙板中部倾斜。为简单有效地替换墙板塑性破坏区，选取V 型界面以下为替换区，用V 型连接梁与上部钢筋混凝土墙板衔接，承受和传递墙体内力。V 型连接界面不仅符合墙板受力特点，而且拥有较大的粘结面，墙内轴压对粘结面剪力传递有增强作用，可使墙底与上部墙板整体性更高。

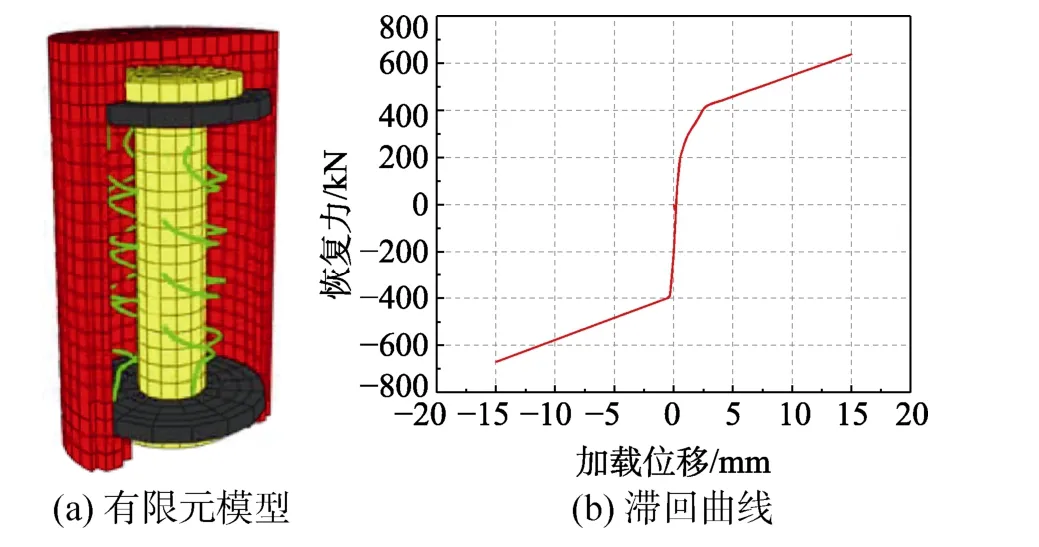
图3 复位支撑有限元模型与滞回曲线 Fig.3 Finite element model and hysteresis curve of self-centering brace

1.3 SC-SW 工作原理及理论骨架曲线

图4 给出了SC-SW 理论骨架曲线。SC-SW 骨架曲线具有双线性特性，在刚度转变处，支撑发生激活，弹性墙底进入第二刚度阶段，导致SC-SW侧向刚度下降，该力学行为与传统剪力墙屈服相似，但此时SC-SW 各部件仍处于弹性状态，称SC-SW 因支撑激活刚度开始下降点为类屈服点。

通过调节弹性墙底两侧支撑第一刚度可调整墙底截面初始转动刚度，可实现替换区域的转动刚度与传统剪力墙相等，使得SC-SW 初始刚度与原墙相等；墙体激活位移由复位支撑设计参数与墙底几何尺寸决定，可依据性能要求确定SC-SW 激活位移大小，做到侧移达到原墙屈服位移时激活；SC-SW 墙底进入第二刚度阶段后墙底转动位移增大的同时内力增长缓慢，上部墙板内力不会激增，仍处于弹性阶段，该过程与传统剪力墙屈服后力学行为相似，通过调节复位支撑第二刚度可对SC-SW激活后刚度和承载力进行设计，做到与原墙承载力相等；由于弹性墙底受力机制清晰，内力解构准确，调节复位支撑有效行程可对墙底转动行程进行设定，从而可对SC-SW 进行延性设计。

剪力墙是高层结构核心受力构件，应尽量不发生损伤。本文提出的SC-SW 旨在实现墙体目标位移下的弹性变形，不以墙体发生塑性变形甚至破坏为代价换取能量消耗能力，墙体在荷载消失后可在弹性墙底的恢复力矩作用下复位，不产生残余位移。

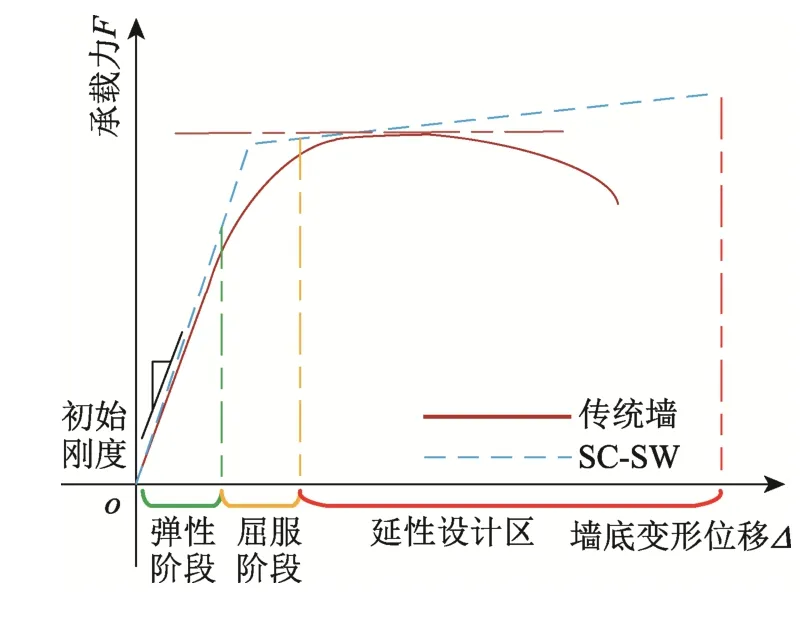
图4 SC-SW 理论骨架曲线 Fig.4 Theoretical skeleton curve of SC-SW

2 SC-SW 滞回性能模拟

2.1 建模方法

在ABAQUS 软件中建立普通SW 和底部铰支SC-SW 的有限元模型，几何尺寸如图5 所示，配筋和材料参数均见参考文献[16－17]。试件SW 轴向受荷为1821 kN，屈服后采用位移控制加载，按位移角为1/275、1/100、1/75 逐级加载，每级加载循环2 次。

混凝土单轴拉压应力-应变曲线采用《混凝土结构设计规范》(GB50010－2010)中建议的曲线，边缘约束区混凝土采用钱稼茹曲线[18]，本构采用塑性损伤模型，塑性损伤因子采用文献[19]中介绍的方法计算。钢筋采用方自虎等[20]开发的适用于模拟钢筋混凝土结构滞回行为的本构模型及材料子程序进行模拟。连接梁与基础梁铰接，采用理想弹性模型进行模拟。

模型中材料属性依据试验实测值确定。钢材性能较优、加工性好，钢部件容易进行弹性设计，因此本文模型中不考虑钢梁和铰接接头屈服。

图5 SC-SW 与SW 构造图 Fig.5 Configuration of SC-SW and SW

2.2 SW 模型验证

试件SW 的破坏形态和裂缝分布如图6 所示。加载过程中，荷载达到一定值时墙板与基础连接界面出现水平裂缝，最外层竖向钢筋继而屈服；随着荷载增大，墙板形成新的水平裂缝并延伸扩展；当荷载达到峰值时，墙脚混凝土压溃剥落，试件承载力开始下降；位移继续增加，墙底混凝土塑性破坏区向中部蔓延，墙体下墩，丧失承载力，最终呈弯曲型破坏形态。

SW 有限元模型如图7(a)所示，与试验滞回曲线[16]对比如图8 所示。模拟所得墙体屈服荷载、峰值荷载和破坏荷载在正向加卸载过程中误差分别为4.26 %、3.60 %和9.23 %，在反向加卸载过程中分别为2.94 %、4.00 %和1.00 %，误差较小。正向加卸载与反向加卸载过程中最大残余位移误差分别为4.8 mm 和2.11 mm。当荷载位移较大时试件墙脚混凝土损伤严重，钢筋与混凝土滑移明显，在试件正向卸载向反向加载交替过程中墙体脚部钢筋由受拉卸载至受压发生屈曲，滞回曲线表现为明显捏缩，而有限元模型对该效应模拟能力有限，引起残余位移存在误差。总体而言，有限元模型与试验实测曲线吻合良好。因此，本文所述建模方法可有效模拟试验试件的力学性能。

图6 SW 破坏形态与裂缝分布 Fig.6 Failure form and crack distribution of SW

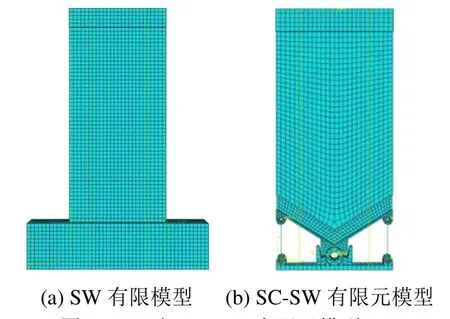
图7 SW 与SC-SW 有限元模型 Fig.7 Finite element models of SW and SC-SW

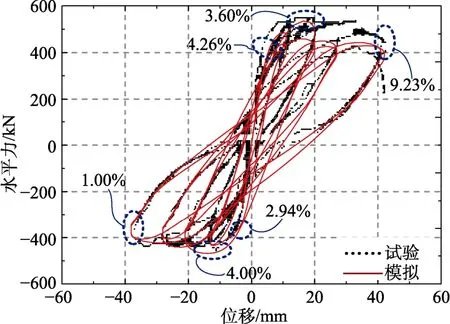
图8 SW 模拟与试验滞回曲线对比 Fig.8 Comparison of hysteresis curves between simulation and experiment of SW

2.3 SC-SW 模型

以等初始刚度和等承载力准则对SC-SW 进行设计。为了将SW 中墙底塑性破坏区域进行有效替换，根据剪力墙塑性铰高度统计经验，SC-SW 中墙底替换区外侧高度h1取600 mm；根据连接梁与基础梁销轴连接构造需求，SC-SW 墙底替换区中间高度h2取200 mm；替换区域厚度t与墙板相同，取160 mm。

采用一维等截面悬臂梁模型对SC-SW 与SW进行对比分析。假设SC-SW 与SW 截面特性相同，则相同荷载作用时候，距基础h1高度处二者截面转角相同，根据SC-SW 与SW 初始刚度相等，由SW初始刚度K0、墙板高度H、截面抗弯刚度EI和截面高度hw确定SC-SW 墙底两侧支撑第一刚度K1：

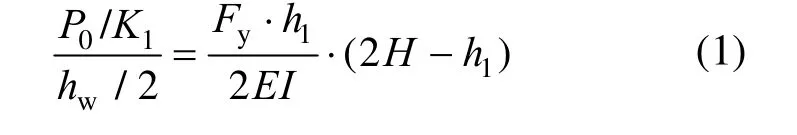
整理得：

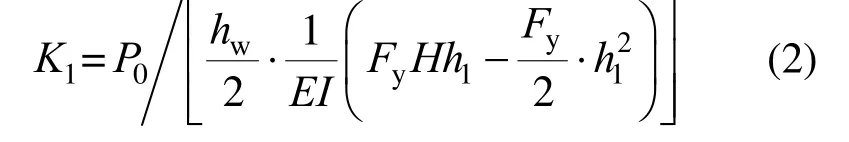
假设SC-SW 在屈服荷载作用下支撑激活，限制SC-SW 类屈服时水平荷载介于SW 屈服荷载与峰值荷载之间(此处选取二者均值)，由SW 屈服荷载Fy与峰值荷载Fp确定支撑碟簧预压力P0，力矩平衡方程有：

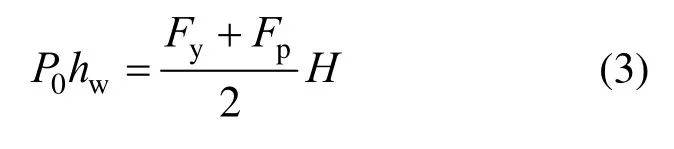
整理得，

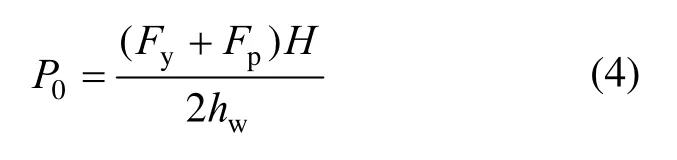
由于SC-SW 支撑激活后内力增长幅度小，假设上部墙板仅发生刚体转动，根据SC-SW 极限位移不小于SW，承载力不小于SW，由SW 峰值荷载Fp和极限位移δu确定支撑第二刚度K2(此处以SC-SW 位移达到δu前最大承载力不低于Fp为条件)，当墙体顶部发生侧移Δ时，有：

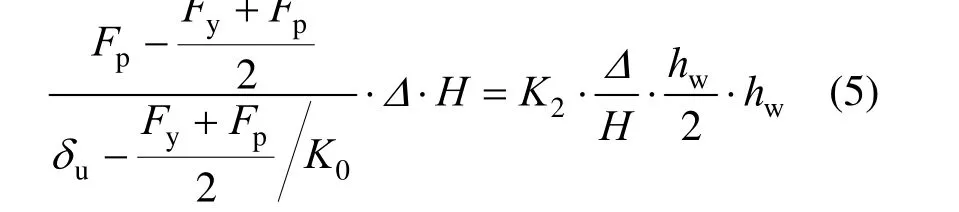
整理得：

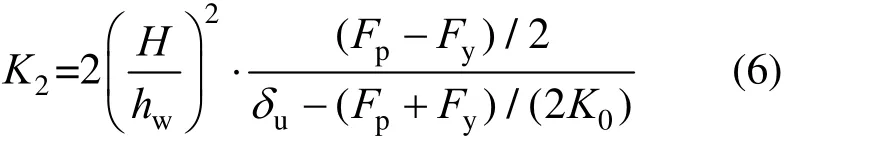
SC-SW 有限元模型如图7(b)所示。墙体几何尺寸参考图5，截面配筋和材料参数设置与SW 一致，连接梁与基础梁仅考虑弹性变形。由于墙底两侧支撑的力学特性简单稳定，通过轴向连接器进行等效模拟，并通过K1、P0和K2值对连接器轴向力与位移关系进行设定。

3 SC-SW 性能对比分析

3.1 滞回性能对比

根据SW 力学性能对SC-SW 进行等效设计，由式(2)、式(4)和式(6)计算K1、P0和K2为1850 kN/mm、925 kN 和24 kN/mm，二者滞回曲线对比如图9 所示。可以看出，SC-SW 滞回曲线具有双线性特性，支撑激活前刚度下降不显著。不同加载幅值下滞回曲线基本重合，包络面积较小，表明墙体损伤程度低。卸载时残余位移较小，复位性能较好。

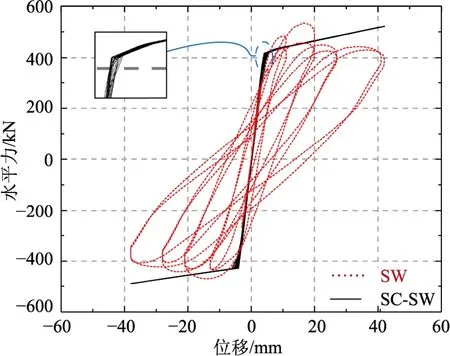
图9 SC-SW 与SW 滞回曲线对比 Fig.9 Comparison of hysteresis curve between SC-SW and SW

SC-SW 与SW 承载能力对比如表1 所示。其中，由等效弹塑性屈服法求得SW 屈服荷载，对应位移为屈服位移。定义SC-SW 由于支撑激活刚度发生转变的点为类屈服点，对应的水平荷载和位移为类屈服荷载和类屈服位移，并与SW 的屈服荷载和屈服位移进行对比。定义SW 峰值荷载的85 %为极限荷载，对应位移为极限位移。由于SC-SW 在受荷过程中未发生刚度下降，定义受荷过程中所受最大荷载为峰值荷载，对应位移为峰值位移，位移角达塑性限制0.02 时的位移为极限位移，对应荷载为极限荷载。可以看出，SC-SW 的类屈服荷载和类屈服位移与SW 相近，二者初始刚度分别为90 kN/mm和86 kN/mm。二者峰值荷载相近，但是SC-SW 在刚度转变后呈现强化特性，没有出现下降段，峰值荷载与极限荷载出现在最大加载位移处。总体来看，SC-SW 滞回曲线与SW 骨架线相近，实现了屈服荷载、峰值荷载和屈服位移的等效设计。定义极限位移与屈服位移的比值为延性系数，用于衡量剪力墙的延性。SC-SW 与SW 延性系数分别为8.92和7.05，提高了26.52 %，表明SC-SW 具有更好的变形能力。

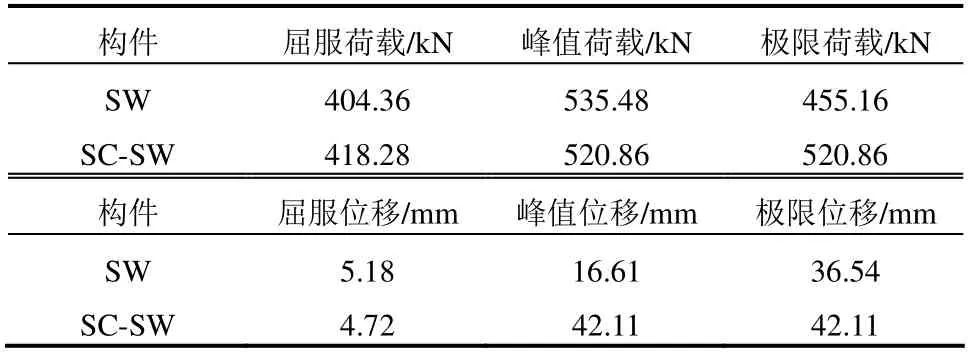
表1 SC-SW 与SW 力学特征对比 Table 1 Comparison of mechanical characteristics between SC-SW and SW

3.2 耗能能力与复位能力对比

不同幅值位移加载过程中SC-SW 与SW 累计耗能对比如图10 所示。从图可以看出，二者累计耗能均随着加载幅值的增加而增加，但SW 累计耗能增加显著，SC-SW 增加缓慢。加载幅值较小时，二者均处于弹性阶段，墙体无损伤，耗能少。随着加载幅值增大，SW 屈服发生塑性变形，墙板裂缝扩展，墙底混凝土进入塑性破坏阶段，墙体损伤逐渐增大，混凝土的塑性变形和钢筋的屈服耗散大量能量。SC-SW 在侧移增加过程中墙底两侧支撑轴力超过碟簧预压力，支撑激活，墙体刚度转变，进入第二刚度阶段。SC-SW 刚度转变时上部墙板混凝土应力应变水平低，未进入塑性破坏阶段，而刚度转变后由于墙底转动，水平荷载增加缓慢，墙体内力不会激增，混凝土大部分仍会处于弹性阶段。SC-SW在发生较大侧移时，上部混凝土和下部墙底主要发生弹性变形，塑性变形和损伤较少，因此几乎不耗散能量。同时表明需要在整体结构中增设耗能装置来耗散因SC-SW 不能发生塑性变形而无法耗散的能量。

SC-SW 与SW 残余位移对比如表2 所示。可以看出，SW 残余位移随加载幅值增加而增大，最大残余位移角达0.58 %，残余变形明显，混凝土破损后修复困难，导致构件丧失完整性无法继续使用。SC-SW 残余位移不超过2 mm，残余位移在加载幅值递增过程中增加缓慢，验证了本文提出的设计方案可实现剪力墙大侧移下的低损伤弹性变形，具有较好的复位能力。

3.3 损伤分布对比

SC-SW与SW在第一次达到峰值荷载和末次循环加载极限荷载作用下混凝土墙板受压损伤(DAMAGEC)分布如图11 所示。

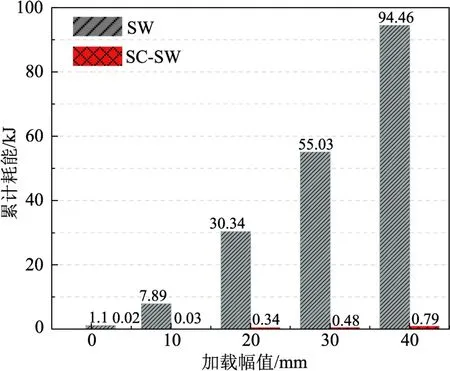
图10 SC-SW 与SW 累计耗能对比 Fig.10 Comparison of accumulative hysteretic energy dissipation between SC-SW and SW

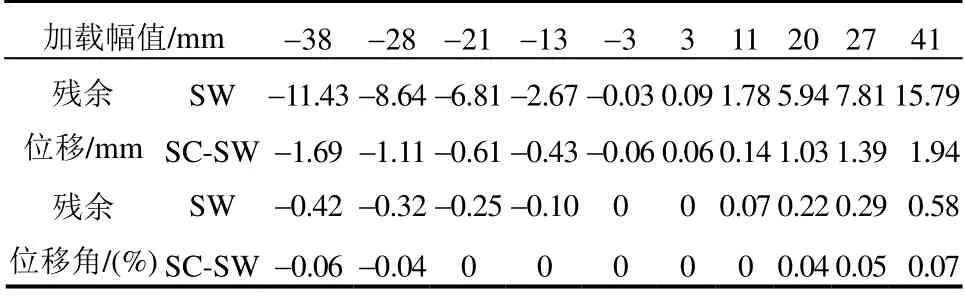
表2 SC-SW 与SW 残余位移对比 Table 2 Comparison of residual deformations between SC-SW and SW

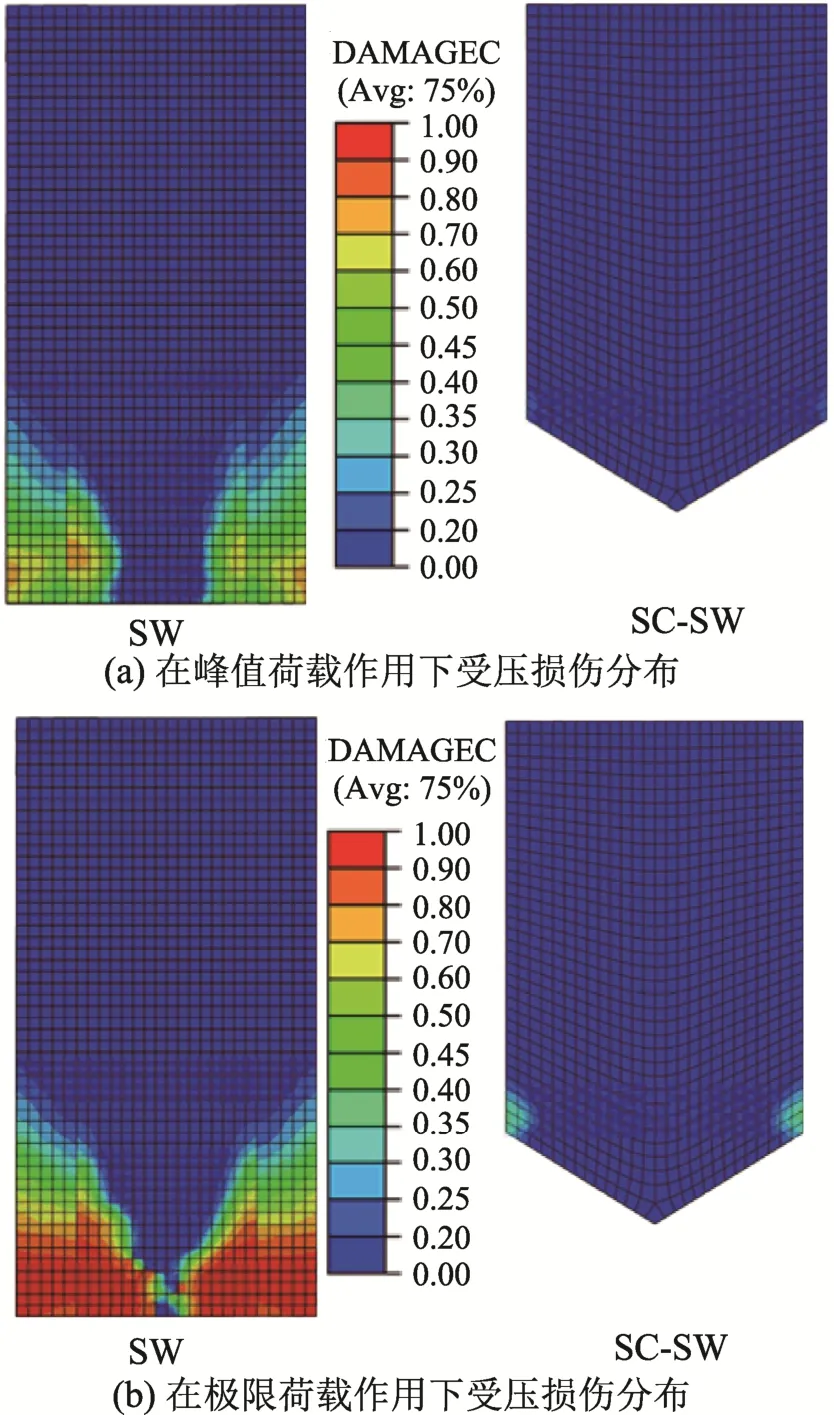
图11 SW 与SC-SW 受压损伤分布 Fig.11 Concrete compression damages of SW and SC-SW

可以看出，SW 受压损伤主要发生在墙底且集中在两侧墙脚，这与试验所记录到的试件破坏现象与弯曲破坏模式一致。峰值荷载作用下，SW 墙脚已经形成一定程度的损伤，而SC-SW 混凝土部分基本没有损伤。极限荷载作用下SW 损伤程度加重，由于反复加卸载，墙脚损伤逐步积累，损伤较大区域与试件试验破坏时底部混凝土压溃剥落区域一致，墙底受损严重，两侧墙脚破坏。而SC-SW 仅在连接梁两端处发生混凝土的轻度损伤。从受压损伤对比可以看出，本文提出的SC-SW 有效地将SW受荷过程中受压损伤严重的区域进行了替换，在水平荷载移除后，SC-SW 由于在上次荷载激励过程中未形成明显受压损伤，混凝土性能保持在健康水平，剪力墙整体功能完整，实现了功能恢复的目的。

SC-SW与SW在第一次达到峰值荷载和末次循环加载极限荷载作用下混凝土墙板受拉损伤(DAMAGET)分布如图12 所示。

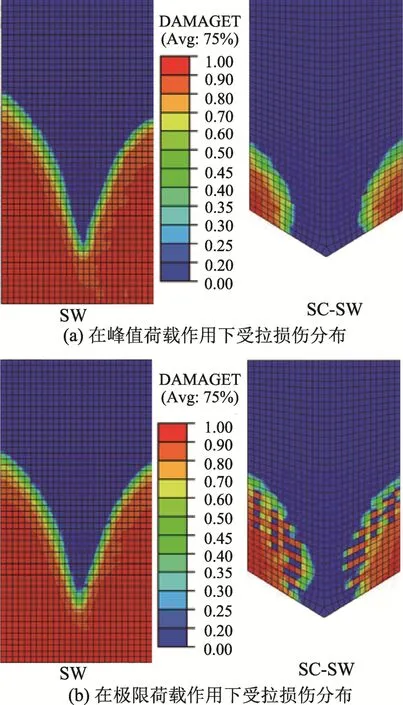
图12 SW 与SC-SW 受拉损伤分布 Fig.12 Concrete tensile damages of SW and SC-SW

可以看出，SW 在经历屈服至极限荷载作用过程中受拉损伤发展不明显，几乎在屈服荷载作用时已达到最高水平，而受拉损伤程度高的区域与试件试验过程中墙板开裂区域一致。由于混凝土是与墙内竖向钢筋共同浇筑，在水平荷载不高时，混凝土与钢筋共同承担墙板拉力，钢筋拉伸，混凝土应力超过受拉极限发生开裂，即使水平荷载递增，受拉裂缝早已形成。而SC-SW 在峰值荷载作用下混凝土受拉损伤程度较轻，加载至极限荷载过程中损伤会逐步发展，损伤区域从连接梁两侧向墙板中部和上部扩展，最终损伤程度比SW 小。因为连接梁可以整体转动，变形过程中对上部墙板有承托作用，梁体自身变形较小，比起SW 同等位置混凝土对上部墙板的作用力，连接梁更均匀，使得上部混凝土受力更均匀，受拉损伤程度降低。

通过受拉损伤和受压损伤对比可以看出，SC-SW 主要减轻的是墙板混凝土受压损伤，对混凝土受拉损伤有一定程度的控制，但还是有一定程度的发展。对于受弯型钢筋混凝土构件，损伤和破坏主要因混凝土受压造成，针对受压损伤进行改善对构件损伤控制效率更高。

4 结论

本文提出一种底部铰支自复位钢筋混凝土剪力墙，并对其构造和工作原理进行了介绍。通过数值模拟对新型自复位墙与普通钢筋混凝土剪力墙的力学性能进行了对比分析，得到以下结论：

(1) 采用碟簧构造的复位支撑与型钢梁组合成弯剪解耦的弹性墙底，对传统剪力墙失效时塑性破坏严重的墙底进行替换后，能实现剪力墙较大侧移弹性变形，残余位移显著降低，复位性能较好。同时可承担较大竖向荷载并提供较大侧向刚度。

(2) 复位支撑具有双线性滞回特性，可使SC-SW 也具有双线性滞回特性。通过对复位支撑的参数调整，可实现SC-SW 与传统墙等初始刚度和等承载力设计。与相同截面传统剪力墙相比，SC-SW 的延性提高了26.52 %，延性设计方便可行。

(3) SC-SW 在变形过程中损伤小破坏轻，通过混凝土开裂和塑性变形方式耗散的能量少，剪力墙性能可在多次激励后保持在健康水平。

(4) SC-SW 有效的减轻了混凝土墙板受压损伤，使剪力墙整体在经历较大变形后仍处于弹性状态。对受拉损伤的发展有迟滞作用，损伤程度得到一定程度的控制。