内置有挡板的矩形水箱阻尼比估算方法比较分析

钟文坤，吴玖荣

(广州大学-淡江大学工程结构灾害与控制联合研究中心，广州大学，广东，广州 510006)

调频液体阻尼器(Tuned Liquid Damper, TLD)作为一种有效的减振耗能装置，具有成本低、便于安装等优势，已经被越来越广泛地应用于船舶、航天、海洋平台、高层建筑等领域[1―3]。当水箱受到较大的外部激励时，容器内的水会发生较大幅度晃动，而激励频率与水箱自振频率接近时，水箱内水的晃动会更加剧烈，进而会影响到结构的使用功能。由于纯水提供的粘性阻尼较小，不能较好地抑制水的晃动，为克服这一缺点，可以通过在水箱内部设置障碍物如格栅、挡板、立柱等来提高TLD系统的阻尼比[4―7]。但水箱内安装障碍物后，在水发生晃荡时，产生的动力特性会非常复杂[8―10]，所以如何较准确地估算出水箱TLD 系统的阻尼比仍是我们值得深入研究的课题。

对于水箱TLD 系统的阻尼比估算，可以采用能量耗散原理和虚功原理两种方法。而对于内置有挡板的矩形水箱TLD 系统阻尼比估算，大多数学者基本上都是采用能量耗散原理进行推导。Warnitchai 等[7]提出矩形水箱底部中央位置垂直安装有单块挡板的阻尼比估算公式，并与纯水箱系统进行对比，发现内置挡板可以较明显提高水箱系统的阻尼比；Isaacson 等[11]分别推导了底部中央位置垂直安装有单块挡板和左右侧壁水平对称安装有一对挡板的矩形水箱线性阻尼比估算公式，分别研究了垂直挡板的高度、水平挡板的安置高度、水深比等因素对系统阻尼比的影响，并与实验结果进行对比，表明所推导的公式具有较好的估算效果；Faltinsen 等[12]利用能量耗散率方法分别推导了底部中央位置垂直安装有单块挡板和左右侧壁水平对称安装有一对挡板的矩形水箱线性阻尼比估算公式，并与Isaacson 所推导的公式进行了对比。Goudarzi 等[13]推导了底部垂直安装有两块挡板和左右侧壁水平安装有一对挡板的矩形水箱线性阻尼比估算公式，并结合实验研究了两块垂直挡板不同间距下的系统阻尼比。而利用虚功原理来估算水箱系统的阻尼比，主要集中对于内置格栅的水箱。Tait 等[14]把矩形水箱视为等效弹簧-质量-阻尼线性系统，推导了随机激励和正弦激励下内置有多块格栅的等效线性阻尼比计算公式，并讨论了不同水深比、不同激励幅度下水箱系统等效阻尼比的大小变化；Deng 等[15]建立了TLD 水箱系统对应的可调谐等效线性力学模型，并推导出具有任意几何形状如平底矩形、垂直圆柱形、水平圆柱形等多种水箱系统的阻尼比估算公式；Love 等[16]利用线性等效模型和非线性四阶模型分别研究了矩形水箱内部置有多排的十字立柱对水箱系统阻尼比的影响，并推导出阻尼比的估算公式；同时为了改进传统的TLD减振性能，他还设计了由TMD 和TLD 组成的新型减振器，并推导了该系统的阻尼比计算公式[17]；Tsao 等[18]提出一种填充多孔介质的新型TLD 系统，建立其等效的力学系统，并推导出其对应的阻尼比计算方法，与经验计算公式相比，该阻尼比计算方法更具为简便。以往研究者基本上均是单独采用能量耗散原理或虚功原理方法推导水箱系统的阻尼比估算公式，但对于此两种研究方法间的区别与联系还少有学者进行过研究，同时激频比也是影响水箱系统阻尼比的一个重要参数，不能忽略。

基于此本文以某一矩形水箱为研究对象，假定水箱受到的底部外加激励为正弦位移(加速度)激励，利用能量耗散原理和虚功原理两种方法，分别推导了底部安装有多块垂直挡板和左右侧壁安装有多组水平挡板的矩形水箱线性阻尼比估算公式，并与已有的实验结果进行对比分析，还分析了激频比对水箱系统阻尼比的影响。

1 基本理论

1.1 流体势流理论

假定水是不可压缩、无粘性及无旋运动的理想流体，则由流体力学[19]可知，水箱内液体的速度势函数φ(x,y,z,t)满足拉普拉斯方程：

忽略y方向，只考虑x、z两个方向的二维矩形水箱，如图1 所示。水的运动需满足如下边界条件：

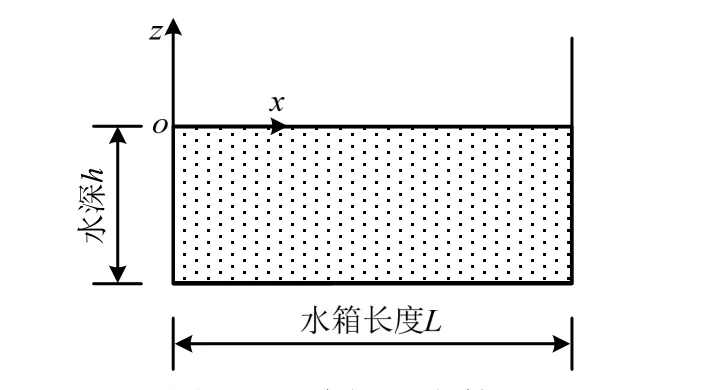
图1 二维矩形水箱 Fig.1 2-D rectangular water tank

水箱左右侧壁(x=0，x=L)：

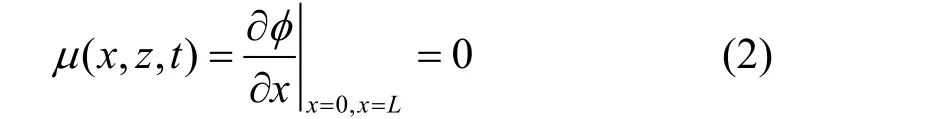
式中， ( , , )u x z t为水的水平运动速度。

水箱底部(z=-h)：

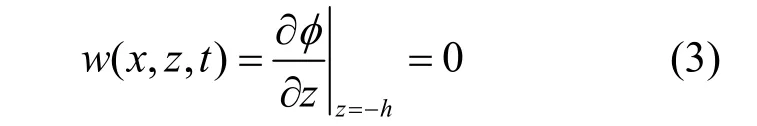
式中，w(x,z,t)为水的竖向运动速度。

对于自由液面的线性化边界层条件为：

联立方程组式(1)～式(4)，满足上述边界条件的速度势函数可以表示为：

1.2 挡板的阻力计算

当水箱受到外部激励作用时，水箱水会产生晃动，根据Morison[20]公式，水箱内的挡板dz段所受到的阻力dF部分可表示为：

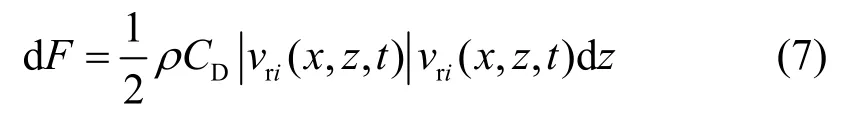
式中：vri(x,z,t)表示为流向挡板的水平入射速度或垂直入射速度；ρ为水的密度；DC表示为挡板的阻力系数，可表示为[12]：

式中：Vrm为vri(x,z,t)的最大值；T为水箱的晃荡周期；lb为挡板的高度。

2 底部安装有垂直挡板的矩形水箱 系统阻尼比分析

只考虑x、z两个方向的维度，对于如图2 所示的仅在底部安装有多块垂直挡板的矩形水箱，在以下推导过程中，假定液体是线性运动且只考虑一阶模态，并忽略挡板对矩形水箱固有频率的影响。

图2 底部安装有垂直挡板的矩形水箱 Fig.2 Rectangular water tank with vertical baffles

2.1 虚功原理

只考虑矩形水箱的一阶晃动模态，把式(5)代入 式(7)，则单块挡板上dz段的阻力dVDiF可表示为：

对速度势函数进行积分，则广义虚水平位移1qδ可表示为：

假定水箱底部安装有n块高度为lb的垂直挡板，则作用在所有挡板上阻力所做的虚功为Wδ：

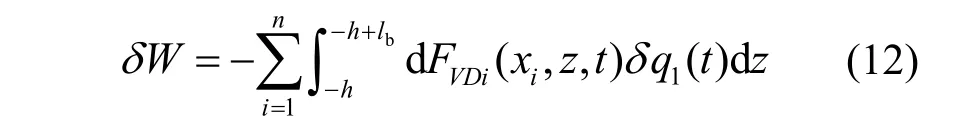
把式(10)、式(11)代入式(12)得：

式中，VnQ为：

式中，VΔ 、VnΘ分别为：

对式(15)进一步化简得：

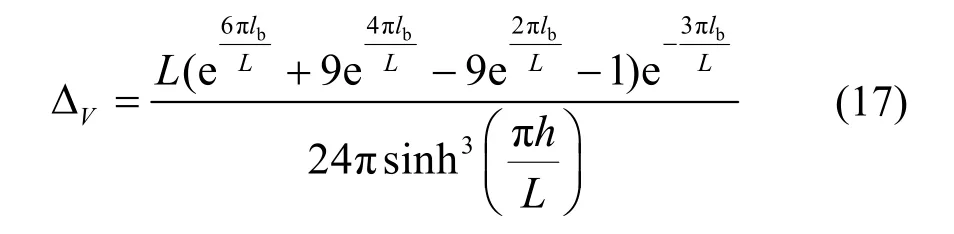
式(14)表示非线性阻尼力，可通过求得与等效线性阻尼力的最小误差来用广义的线性阻尼力代替，非线性与线性阻尼力的误差ε可以表示为[21]：

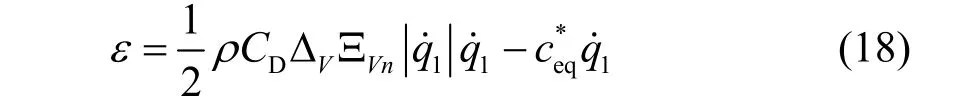
最小误差应满足：

式中，E( )表示期望值，对该式进一步化简，可得广义线性化阻尼：

水箱在正弦激励作用下，线性的广义阻尼可进一步表示为：

式中，q为液体一阶晃动模态下的广义波高幅值。则线性化的广义阻尼比表示为：

Tait[22]等把水箱内的液体视为等效质量块，建立了等效线性化的弹簧-质量-阻尼系统，如图3 所示。该系统在一阶模态下，运动方程为：

式中：X˙˙表示水箱底部外加激励的加速度；rx表示等效质量块相对于水箱的位移，其等效质量、等效阻尼和等效刚度分别表示为式(24)～式(26)[7]：

图3 水箱TLD 等效力学模型 Fig.3 Equivalent mechanical model of a TLD system

式(26)中，1ω为水箱一阶固有频率：

对式(23)进行化简得：

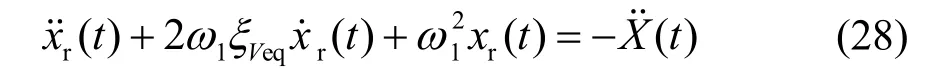
矩形水箱的等效阻尼比可表示为[23]：

式中，Γ为模态参与因子，可表示为[17]：

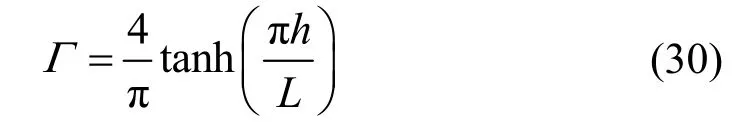
基于虚功原理，可得到底部安装垂直挡板的矩形水箱的线性阻尼比 eqVξ计算公式，即：

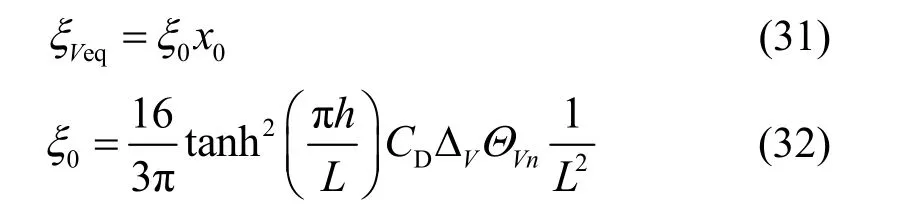
式中，x0为矩形水箱对应的等效线性模型的相对水平位移幅值，可表示为式(33)[14]：

式中，X0为底部正弦激励的位移幅值。

2.2 能量耗散原理

为便于计算矩形水箱的能量耗散率，假设水箱底部无外部激励时，单块挡板以速度uri(x,z,t)在四周静止的液体中做周期为T的振荡运动，则单块挡板所做的功ViW为：

若矩形水箱底部垂直安装有n(n= 1,2,…) 块挡板，则一个振荡周期T内水箱系统的能量耗散率DBV等于所有挡板做的功除以T[12]，即：

挡板对于箱内液体的相对水平速度可表示为：

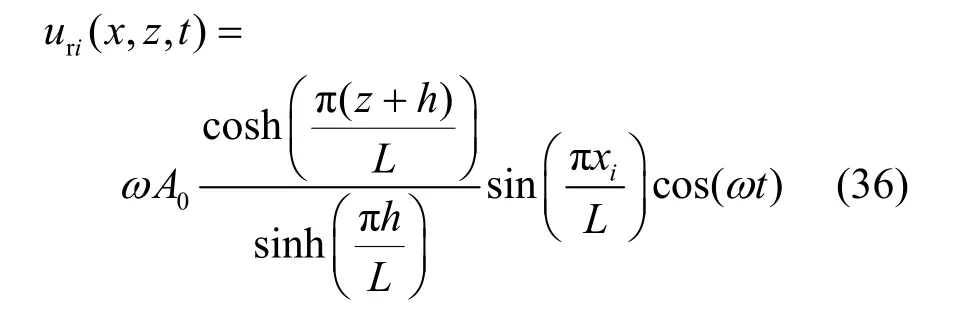
式中，A0为水箱侧壁的最大波高幅值。把式(36)代入式(35)中，得：

分别再对式(39)和式(40)进一步化简得：

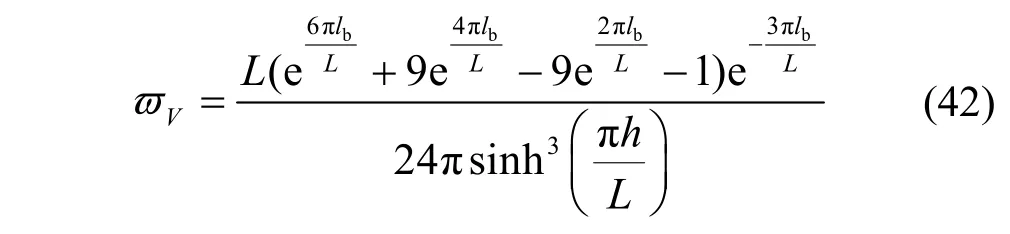
在水箱内，能量耗散率DBV等于液体动能和势能的衰减速率E-˙[12]，即：

式中，E为动能和势能的总和，对于二维的矩形水箱且液体流动是线性的，则可表示为[12]：

另 1=ω ω，可得到底部安装有垂直挡板的矩形水箱线性阻尼比Vξ计算公式，即：

3 侧壁上安装有水平挡板的矩形 水箱系统阻尼比分析

只考虑x、z两个方向的维度，对于侧壁安装有多块水平挡板的矩形水箱，如图4 所示。以下推导过程中，假设的条件与仅有垂直挡板的情形一致。

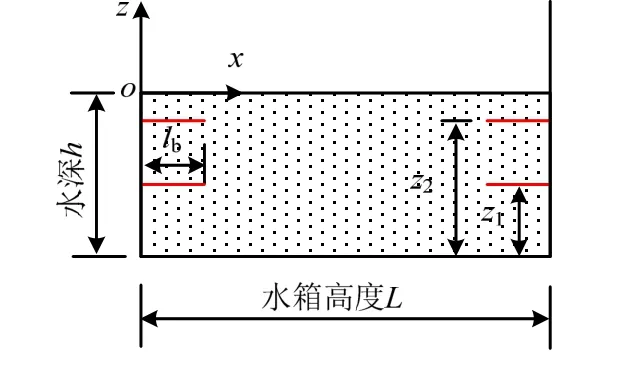
图4 侧壁安装水平挡板的矩形水箱 Fig.4 Rectangular water tank with horizontal baffles

3.1 虚功原理

把上一节矩形水箱底部安装有垂直挡板的阻尼比推导方式，推广到水箱侧壁上安装有水平挡板的工况，则挡板上dx段的阻力dHDiF可表示为：

对速度势函数进行积分，则广义虚水平位移1qδ可为：

若水箱左右侧壁对称安装有2n(n= 1,2,… ) 块水平挡板，则所有阻力所做的虚功δW为：

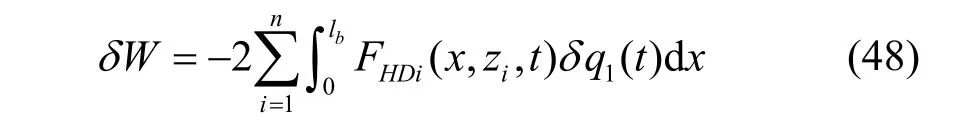
把式(46)～式(47)代入式(48)得：

式(49)中，HnQ为：

式(50)中HΔ 、HnΞ分别为：

当矩形水箱底部受到正弦激励时，与带垂直挡板工况的推导方法类似，用广义线性化阻尼力来代替非线性阻尼力，最后得到矩形水箱左右侧壁对称安装水平2n(n= 1,2,…) 块挡板的线性阻尼比ξHeq计算公式：

3.2 能量耗散原理

同理，把底部安装垂直挡板的矩形水箱阻尼比推导方法，推广到侧壁安装有水平挡板，若水箱左右侧壁对称安装有2n(n= 1,2,…) 块水平挡板，则所有挡板在一个振荡周期T内的能量耗散率DBH可以表示为[3]：

挡板对于箱内液体的相对垂直速度wri(x,z i,t)可表示为：

把式(54)代入式(55)中，得：

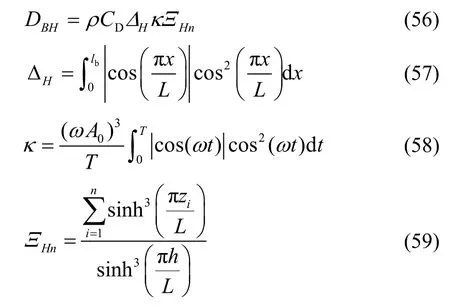
在水箱内，能量耗散率DBH等于液体动能和势能的衰减速率E-˙[12]，即：

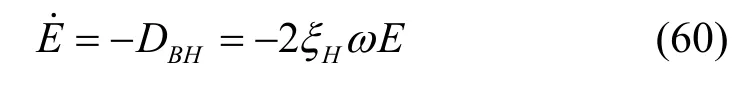
另ω=ω1，则矩形水箱左右侧壁对称安装有2n(n= 1,2,…) 块水平挡板的线性阻尼比ξH计算公式可化简为：

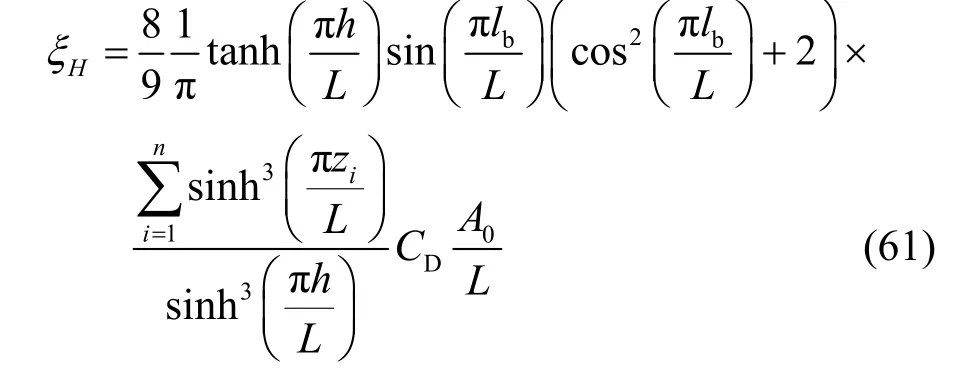
4 结果分析

由上述的推导结果可知，当矩形水箱受到正弦激励时，利用能量耗散原理推导的公式中，水箱侧壁的波高幅值A0是影响阻尼比大小的其中一个主要因素，而利用虚功原理推导的公式中，没有体现出侧壁波高幅值的影响，取而代之的是矩形水箱等效线性模型的相对水平位移幅值x0，而x0又与外激励幅值X0有关。为进一步分析两种方法的差异性，引入矩形水箱等效线性模型的相对水平位移xr与液体波高q的关系式[16]：

若已知水箱侧壁波高幅值A0，则由式(62)进一步得到x0，即：

把式(63)代入式(31)化简得到：

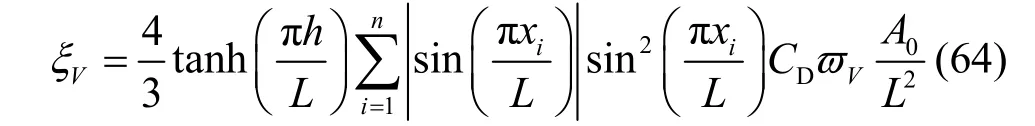
同样，把式(63)代入式(53)进行化简可得到：

可见通过以上的化简，式(64)与式(45)一致，式(65)与式(53)一致，即利用能量耗散原理推导的公式与利用虚功原理推导的公式具有一致性。所以，若已知作用在水箱底部的外加位移激励幅值X0，直接利用虚功原理推导的公式来计算矩形水箱的线性阻尼比会更加方便，若由实验直接测得水箱侧壁的波高幅值A0，利用能量耗散原理推导的公式来计算矩形水箱的线性阻尼比会更加简便。但是需要注意的是，从利用能量法推导的计算公式来看，阻尼比的大小没有直接体现出与激频比的关系，而隐含在波高幅值A0中，而利用虚功原理将TLD 等效线性化后推导的阻尼比计算公式却能直接通过x0体现出与激频比的关系。

当挡板的尺寸较小时，由挡板所产生的阻尼也比较小，在此种情况下则不能忽略水的粘性阻尼影响，此时仅由水产生的阻尼比计算公式为[24]：

式中：ν为水的粘度性系数；b为水箱的宽度；SC为水的表面光滑因子，通常取1。

4.1 实验结果对比

为进一步验证本文所推导的公式的准确性与否，本小节将与Isaacson[11]测得的实验结果进行对比。Isaacson 利用振动台对矩形水箱开展了试验，如图5 所示，矩形水箱为有机玻璃制作，被固定在台面上，当水箱受到荷载激励时水会发生晃动，其阻尼比可以通过侧壁处自由液面波高的自由振动衰减曲线计算得到，而水箱侧壁处自由液面的波高则通过波高仪测量得到。

图5 矩形水箱振动台实验图 Fig.5 View of tank model mounted on shake table

矩形水箱受到的荷载激励为正弦位移激励，且激励频比μ=1，水箱尺寸为0.5 m×0.5 m×0.5 m，水深比h/L=0.5，侧壁对称安装的水平挡板尺寸为lb=40 mm，进行了水平挡板在相对位置为0.6h、0.7h、0.8h的三组实验；水箱底部安装的垂直挡板位于L/2 处，进行了垂直挡板高度为0.1h、0.2h、0.3h的三组实验；对于侧壁对称安装水平挡板的水箱，实验测得的侧壁波高幅值为0.1h，对于水箱底部安装垂直挡板的水箱，实验测得的侧壁波高幅值为0.2h，对比结果如图6～图7 所示。

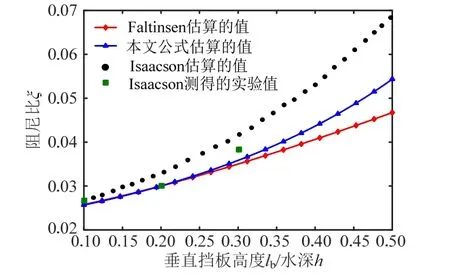
图6 线性阻尼比随垂直挡板高度变化的实验值与 预测值比较图(垂直挡板) Fig.6 Variations of predicted and measured linear damping ratios with various relative vertical baffle heights (h/L=0.25)

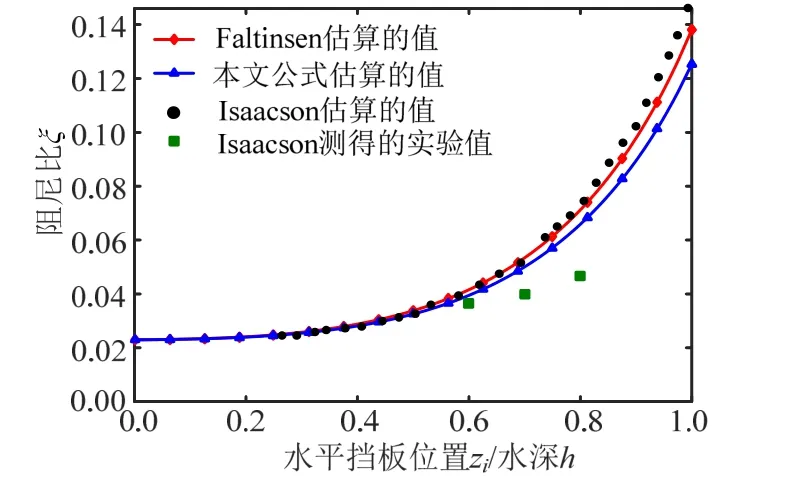
图7 随挡板相对位置变化的线性阻尼比实验值与 预测值比较图(水平挡板) Fig.7 Variations of predicted and measured linear damping ratios with various relative horizontal baffle locations (h/L=0.25 and lb/L=0.08)

由图6 可知，对于底部安装有单块垂直挡板的矩形水箱线性阻尼比，其值随挡板高度的增大而增大；当垂直挡板相对高度lb/h＜0.35 时，用本文公式估算的值与 Faltinsen 估算的值比较接近，当lb/h＞0.35 时，用本文公式估算的值要大于Faltinsen估算的值，而这两者值在0.1＜lb/h＜0.5 上都小于Isaacson 估算的值；在lb/h=0.1 处，本文公式估算的值、Isaacson 估算的值与Faltinsen 估算的值基本上与实验值一致，在lb/h=0.2、lb/h=0.3 处，本文公式估算的值与Faltinsen 估算的值较接近于实验值，而Isaacson 估算的值要大于实验值。

由图7 可知，对于侧壁安装对称水平挡板的矩形水箱线性阻尼比，其值随挡板相对高度位置的增大而增大；当水平挡板位置z＜0.6h时，利用本文公式估算的值、Isaacson 估算的值与Faltinsen 估算的值，三者基本一致。当z＞0.6h时，利用本文公式估算的值要小于Isaacson 与Faltinsen 估算的值；挡板位置z在0.6h处，三者所估算的值基本与实验值基本一致，但在0.7h、0.8h处，本文公式所估算的值要小于其他两者的值，而三者的值都要大于实验值。其主要原因可能是挡板靠近液面时，会出砰击现象，而使得用线性阻尼比估算的公式会高估矩形水箱的阻尼比。由图6～图7 可知，与安装垂直挡板相比，安装水平挡板会产生更高的阻尼比。

由上述可知，本文利用能量耗散原理与虚功原理两种方法，所推导的矩形水箱的线性阻尼比计算公式具有较好的估算效果。

4.2 激频比对阻尼比的影响

激频比也是水箱阻尼比的重要影响因素之一，根据式(31)、式(53)，以下给出不同激频比作用下矩形水箱的阻尼比值，假定水箱的尺寸为0.5 m× 0.5 m×0.5 m，外激励为正弦激励且激励幅值为20mm，结果如图8 所示。

图8 不同激频比作用下矩形水箱的线性阻尼比估算值 Fig.8 Variation of predicted normalized damping ratio with various frequency ratios

由图8 可知，当激频比μ=1 时，分别安装有垂直挡板和水平挡板的矩形水箱的线性阻尼比都达到最大值，而在μ=0.9～1.0、μ=1.0～1.1 两个区间内，阻尼比变化幅度较剧烈，说明激频比对矩形水箱的阻尼比影响较大，不可忽视，而直接采用激频比μ=1.0 时的值，很容易高估矩形水箱的阻尼比值。

4.3 能量耗散原理对比

本文在利用能量耗散原理推导矩形水箱的线性阻尼比公式时，采用的方法是借鉴于Faltinsen 的推导方法，但两者之间又存在一定的差异性，忽略水的粘性阻尼，下面对此进一步分析。

4.3.1 底部安装有垂直挡板的水箱系统阻尼比

Faltinsen[12]利用能量耗散原理推导了水箱底部安装有单块垂直挡板(挡板在x=L/2 位置处)的阻尼比计算公式，表示为：

在Faltinsen 的推导过程中，简化了挡板z方向上的速度计算方法，并采用z= -h处的速度值代替挡板任意z方向上的速度值。在本文第2.2 小节，在推导水箱底部安装有任意块垂直挡板的矩形水箱的阻尼比过程中，考虑了液体x方向的相对水平速度沿z方向的变化，为比较两公式之间的差异，令式(64)中x=L/2 则可化简为：

以下给出两种方法计算底部安装有单块垂直挡板的矩形水箱的归一化阻尼比随水深比变化的曲线图，如图9 所示。

图9 矩形水箱底部垂直挡板高度引起的归一化阻尼比随水深比变化的比较图 Fig.9 Variation of normalized damping ratio with various liquid depth ratios and different vertical baffle heights

由图9 可知：当lb/h位于某一定值时，由图9(a)～图9(c)可以看出，采用本文推导的公式估算的系统阻尼比与Faltinsen 估算的值相比，两者之间的差值与外加激励的最大波幅无关；由图9(d)可知，挡板的高度小于0.2h时，本文推导的公式估算的值与Faltinsen 估算的值基本一致；挡板的高度大于0.2h时，Faltinsen 计算的值小于本文计算的值，两者之间的差值随lb/h的增大而增大。显然，当挡板的高度较大时，考虑液体x方向的相对水平速度沿z方向的变化来估算水箱的阻尼比会更加合理。但垂直挡板高度较大时，采用本文公式估算来水箱的线性阻尼比时，还需考虑挡板对水箱最低固有频率的 影响。

4.3.2 侧壁安装有水平挡板的水箱系统阻尼比

同样，Faltinsen[12]在推导矩形水箱左右侧壁安装两块水平挡板(挡板在zi=Hbi位置处)的阻尼比计算公式过程中，简化了挡板x方向上的速度计算方法，并统一采用挡板在x=0 处的速度值代替其沿x方向的变化，最终表示为：

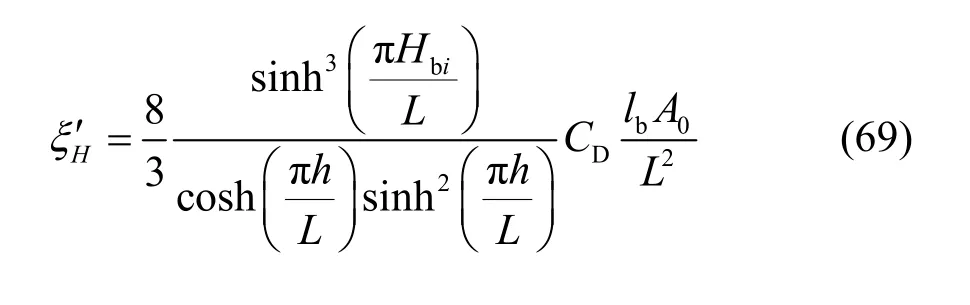
在本文第3.2 小节中，在推导水箱阻尼比计算公式过程中，考虑了液体z方向的相对速度沿x方向的变化与激频比的影响，为比较两公式之间的差异，令式(50)中zi=Hbi则可化简为：

以下给出两种方法计算水箱左右侧壁安装有两块水平挡板时，水箱系统对应的归一化阻尼比随水深比变化的曲线图，如图10 所示。

图10 矩形水箱侧壁水平挡板引起的归一化阻尼比 随水深比变化的比较图 Fig.10 Variation of normalized damping ratio with various liquid depth ratios and different horizontal baffle lengths

由图10 可知，当lb/L=0.05 时，本文推导的公式计算的值与Faltinsen 计算的值基本一致；当lb/L增大至0.15 时，本文推导的公式计算的值小于Faltinsen 计算的值，两者之间的差值随Hb的增大而越来越明显。显然，当lb的长度越来越大时，液体z方向的相对速度沿x方向的变化也越来越明显，进而对水箱的阻尼比影响也越来越大，所以考虑该因素的影响来估算水箱的阻尼比会更加合理。但水平挡板长度较长时，采用本文公式来估算水箱的线性阻尼比时，还需要考虑挡板对水箱最低固有频率的影响。

5 结论

通过以上对于内置有水平和垂直挡板的矩形水箱受到正弦激励时的线性阻尼比研究，得到以下结论：

(1) 对于底部安装垂直挡板的矩形水箱和左右侧壁安装对称水平挡板的矩形水箱，本文分别采用能量耗散原理和虚功原理对其线性阻尼比估算，两种不同方法推导的结果具有一致性，且具有较好的估算效果，在利用本文所建议的公式时，可以根据外加激励幅值还是水箱侧壁波高幅值为已知条件，来选用相应的内置有水平和垂直挡板的水箱TLD系统线性阻尼比估算方法；

(2) 在外加激励和其它条件相同的情况下，水箱侧壁安装水平挡板同比底部安装垂直挡板相比，前者可以产生更高的线性附加阻尼比；

(3) 激频比对矩形水箱的阻尼比影响较大，不可忽视，而直接采用激频比μ=1 时的值，容易高估矩形水箱的阻尼比值。

(4) 采用能量耗散原理推导矩形水箱的线性阻尼比公式，本文考虑了设置垂直挡板时液体x方向的相对水平速度沿z方向的变化，或是设置水平挡板时液体z方向的相对速度沿x方向的变化，以此来估算水箱的线性阻尼比，同Faltinsen 的建议公式相比，得到的阻尼比估算结果更加合理。