用弯矩分量求三次样条插值函数的弯矩
刘远鹏,刘光好,金少华
(1.河北工业大学 工程训练中心,天津 300401;2.河北工业大学 土木工程学院,天津 300401;3.河北工业大学 理学院,天津 300401)
用弯矩分量求三次样条插值函数的弯矩
刘远鹏1,刘光好2,金少华3
(1.河北工业大学 工程训练中心,天津 300401;2.河北工业大学 土木工程学院,天津 300401;3.河北工业大学 理学院,天津 300401)
根据参考弯矩图解法原理,将相邻节点函数差和节点函数的导数变换为侧移分量和转角分量.利用各区间转角分量、侧移分量与函数的二阶导数形成弯矩-位移方程,以及连续梁支座相邻两跨转角方程,结合连续梁弯矩图的性质分析样条插值函数,做参考弯矩图;由此得到三次样条插值函数的支座弯矩.通过算例说明未知量参考弯矩图、荷载参考弯矩图、转角分量图和侧移分量图的使用方法.
特征点;转角分量;侧移分量;参考弯矩图;三次样条插值函数
三次样条插值函数有广泛应用[1-3],且有各种表达方法[4-5],计算方法也多种.文献 [4]则采用构造三角阵的逆阵方法简化节点等距问题.通常可以将三次样条插值函数比拟为连续梁的挠曲线;其二阶导数视为连续梁的弯矩.因此三次样条函数的二阶导数分布就相当于无荷载作用有支座沉陷的抗弯刚度EI=1(本文采用无量纲)的连续梁弯矩图.用力学计算这种连续梁方法很多,可以利用广义图乘法及其弯矩分量[4-7]分析连续梁的原理.利用连续梁弯矩图和单跨梁弯矩图(分别是结点位移弯矩图和杆端位移弯矩图.在不致混淆时的也简称为弯矩图)的性质;求弯矩图从而获得结点弯矩,从而产生插值函数.整体计算过程简单,力学意义清楚.其计算量也得到优化.
1 弯矩分量与连续梁结点转角方程
首先分析节点区间内的插值函数(这相当于单跨梁的挠曲线).如下常见表达式:

根据结构力学常用方式,对三次样条函数的连续梁称弦转角为:


左右两端的转角分量[5-6]

统称这3个量为梁弯矩的位移分量,即弯矩分量.称梁内1/3点和2/3点分别为左特征点和右特征点[5-6];设为L点和R点.利用式 (1)计算特征点的弯矩,与位移分量比较:

这2个方程是梁的弯矩-位移方程,是梁的普遍形式的简化[5].
因连续梁相邻两跨的杆端转角分量表达式不同,但是杆端连接有相同转角,则:

这个方程为连续梁的结点转角方程[7].
根据样条函数的二阶导数,相邻两跨的特征点弯矩Mk1+1/3、Mk1+2/3与杆端的弯矩Mk1、Mk有如下的关系:

由此可知,弯矩分量有2种,它们是特征点的弯矩分解.若梁的弦转角和杆端转角为正方向,那么弯矩分量可用图1方法表示.
连续梁弯矩图的性质:
1)区间内2个特征点的侧移分量数值相同,分别在杆的上下两侧,与弦转角方向一致.如图1a).

图1 特征点上的弯矩关系Fig.1 Relationship ofmomenton characteristic point
2)转角分量的方向分别与其所表示的转角方向一致.如图1b).
3)在每个区间内,弯矩图是直线,如图1c).
4)特征点的弯矩及其分量满足梁的弯矩-位移方程和连续梁结点转角方程.连续梁相邻两跨的转角分,如图1d).
只要区间内插值函数是三次多项式;无论采用那种表达式等,上述性质都成立.而分析样条函数过程中,对结点转角的估计相当于对特征点的转角分量的估计.
2 参考弯矩图分解与弯矩分量图
2.1 参考弯矩图分解
计算过程中连续梁弯矩图是用已知量和未知量共同表示的,则为区别称其为参考弯矩图(用M表示).那么据线性关系,将参考弯矩图M分解为[6]:

荷载参考弯矩图是利用连续梁的支座位移和一个已知条件(一端的已知弯矩或转角)计算形成;且表达式不含未知量.而未知量参考弯矩图根据参考弯矩图的未知量计算形成的弯矩图;不含已知条件(位移条件或杆端弯矩条件).其各弯矩表达式是x的一次齐次式.
荷载参考弯矩图和未知量参考弯矩图都是杆内无荷载的连续弯矩图,则在每个弯矩图内分别具有连续梁弯矩图的上述4条性质.对于具体的计算过程来说,的值由已知的边界条件和0到n的xk,yk的值确定;这样对于来说yk的值全为0,则也全为0,带入式 (6)、式 (7)后得,,根据公式后得.
根据三次样条插值函数连续梁弯矩图的上述性质,通过作参考弯矩图方法求支座弯矩.将支座弯矩代入公式 (1)就生成区间内三次插值样条函数.
2.2 弯矩分量图与算例
已知函数值分布如表1所示[8].
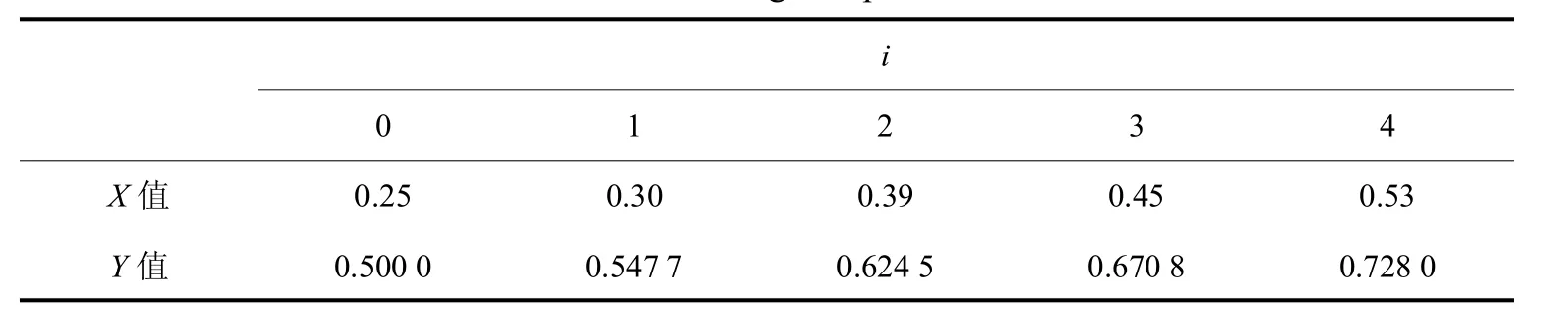
表1 节点数值Tab.1 Digiton point
根据支座位移计算侧移分量:
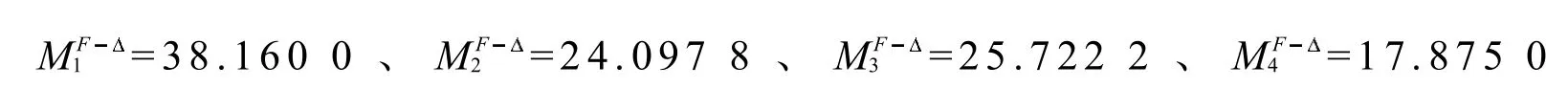
将它们标在连续梁上形成侧移分量图,如图2a).
提取图2a)和图2b)的位移分量和转角分量,根据式 (6)计算第1跨的L点弯矩:

作荷载参考弯矩图.将1跨 L点弯矩标在连续梁上,如图3a).因最左端弯矩等于0,根据式 (9)、式 10,作第1跨参考弯矩图直线,产生R特征点和右端的弯矩,如图3a).
根据式 (7)转角分量
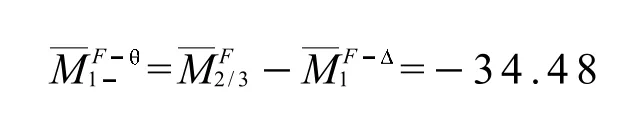
将其标在转角分量图上,如图2b).
利用结点转角方程计算第2跨左端转角分量,如图2b).
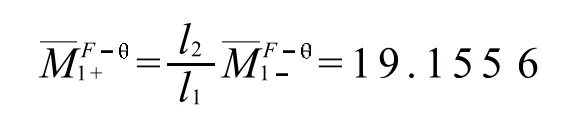
同理依次分析第2跨和第3跨的杆端弯矩和特征点的弯矩;依次产生各跨参考弯矩图直线.同时得到转角分量的分布.如图2b)(称其为转角分量图).因此荷载参考弯矩图如图3a)所示.
根据未知量假设作未知量参考弯矩图.
这个图的A端转角等于0,且无侧移;则各个特征点弯矩等于转角分量.
利用A端弯矩等于未知量x,A端转角分量等于0作第1跨弯矩图,如图3b).
利用特征点未知量参考弯矩与杆长成反比关系,则
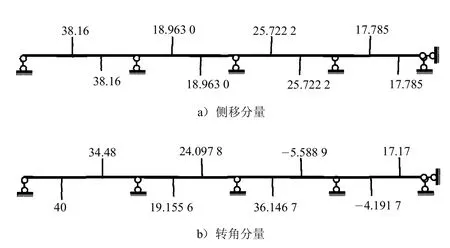
图2 弯矩分量的分布图Fig.2 Distribution ofmomentcomponent
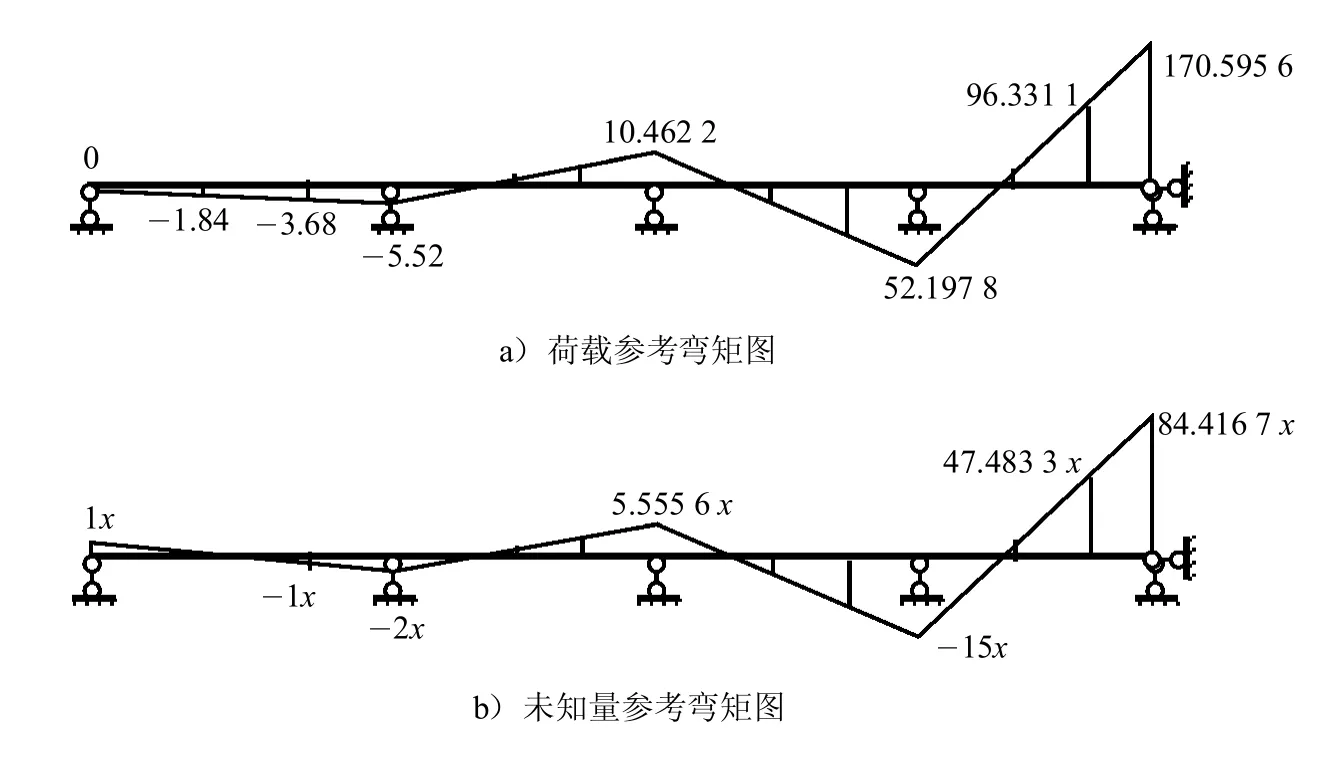
图3 参考弯矩图求三次样条插值函数Fig.3 Reference BMD for cubic spine interpolation function
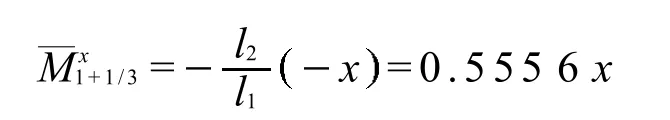
依次作第2跨、第3跨和第4跨的未知量参考弯矩图,如图3b).
荷载参考弯矩图与未知量参考弯矩图相加形成参考弯矩图.因第4跨的右转角分量和侧移分量是已知量,其和是R特征点弯矩;与参考弯矩图的特征点弯矩比较表达式建立方程:
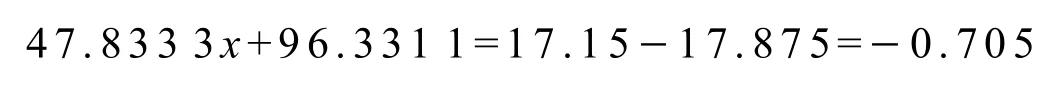
因此x=-2.028 6,计算各杆端的弯矩值,用式 (11)计算各杆端的支座弯矩:
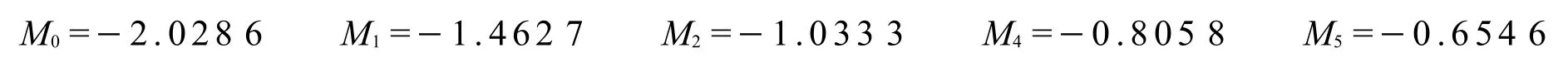
最后结果与其它方法一致.
具体计算过程中,由于各个分量均有系数2,可以先将系数2提出,最后得到的数值乘以2以获得各段点弯矩.这样可以进一步简化计算过程.
如果左端边界条件与此例相同,那么所需未知量以及建立的参考弯矩图的形式可不变;而依据右端边界条件建立不同的方程.对于第2种边界条件和第3种边界条件也可以用类似的方法求解.
2.3 算例的MATLAB程序


S为边界条件,com_la为侧移分量,com_l为左端转角分量,com_r为右端转角分量,MF为荷载弯矩(l为左端,r为右端),Mx为未知量弯矩(l为左端,r为右端),M为每个结点的弯矩.
3 结论
本文利用连续梁参考弯矩图解法形成分析计算三次插值样条函数的连续梁结点弯矩方法.其中利用参考弯矩图的两个层次分解:荷载 未知量图分解,以及弯矩位移分量图分解.利用了梁的特征点的弯矩的侧移分量、转角分量,以及弯矩 位移方程和连续梁结点转角方程.通过未知量参考弯矩图、荷载参考弯矩图、转角分量图和侧移分量图分析产生未知量方程,进一步得到三次插值样条函数的连续梁结点弯矩.计算过程仅需一个未知量,具有明显的并行计算特点.
[1]陈盛,赵东标,陆永华,等.基于二维轮廓点云的螺纹中径计算 [J].光学精密工程,2015,23(6):1791-1799.
[2]常景娜,高慧斌,乔冠宇.一种基于传感器的测量目标运动参数方法研究 [J].传感器与微系统,2015,34(11):19-22.
[3]梁栋,刘良栋,何英姿.月球精确软着陆最优标称轨迹在轨制导方法 [J].中国空间科学技术,2011(6):27-35.
[4]Moon BS.Anexplicitsolution for thecubic spline interpolation for functionofasinglevariable[J].Applied Mathematicsand Computation,2001,117(2-3):251-255.
[5]刘光好,赵光鉴.刚架参考弯矩图解法的侧移问题 [C]//崔京浩.第十一届全国结构工程学术会议论文集(VolⅠ).长沙,2002:395-398.
[6]刘光好,张扬,王俊杰,等.连续梁支座反力、弯矩、位移及三支座反力方程 [J].公路交通科技(应用技术版),2007,31(3):106-108.
[7]Liu Guanghao,Yang Shaobin,LiuYuanpeng.Three-columniationendmomentequationof framewithsupportsinkageand angle[C]//2011INternationA l Conferenceon Remote Sensing,Environmentand Transportation Engineering(Vol5).Nanjing,2011:4670-4682.
[8]朱晓临.数值分析 [M].合肥:中国科学技术大学出版社,2010:148-150.
[责任编辑 杨 屹]
Themomentcomponent formomentof cubic spline interpolation function
LIU Yuanpeng1,LIU Guanghao2,JIN Shaohua3
(1.Engineering Training Center,HebeiUniversity of Technology,Tianjin 300401,China;2.SchoolofCivilEngineering and Transportation,HebeiUniversity of Technology,Tianjin 300401,China;3.Schoolof Sciences,HebeiUniversity of Technology,Tianjin 300401,China)
According to theory of referencebendingmoment,the difference of function atpointbetween neighbor points and derivative of function atnodeare translated into sideway componentand angle component.The sideway component, angle componentand the second derivativeof the function assemblemoment-deflection formula in each section.Themoment-deflection formulaand the cornerequation between adjacentspan on continuousbeam combinedw ith referencebendingmomentdiagram are used for solving Cubic Spline Interpolation function.The example in article illustrates using methodsof the load referencebendingmomentdiagram,theunknown referencebendingmoment,thesideway component and the angle componentdiagram for solving.
characteristic point;angle component;sideway component;reference bendingmomentdiagram;cubic spline interpolation function
TU311.4
A
1007-2373(2016)04-0093-06
10.14081/j.cnki.hgdxb.2016.04.015
2015-11-19
河北省高等学校科学技术研究重点项目(ZD2014051)
刘远鹏(1984-),男(汉族),实验师.
:刘光好(1948-),男(汉族),副教授.

