理解教材内涵,创造利用资源
刘婷婷
[摘 要] 只有充分挖掘教材内涵并进行新的理解、开发和利用,才能将其价值与功能充分发挥出来. 教师一定要从多个角度对教材进行理解和创造,并且将新课程理念充分体现在教学设计与教学实施的过程中,使学生获得更为广阔的视野、充分的学习资源、思维的启发,从而实现数学能力的提升.
[关键词] 教材;理解;创造意识;概念教学;学习方法;解题
为学生数学学习活动提供学习主题、基本线索、知识结构的数学教材是实施数学教学、达成数学目标的重要资源. 担当着数学课程理念基本物化形式这一重要角色的教材,也是学生学习数学、教师教授数学的蓝本. 充分凝聚智慧结晶的教材往往能将数学学科的价值完整而充分地体现出来. 只有充分挖掘教材内涵并进行新的理解、开发和利用,才能将其价值与功能充分发挥出来. 而且,对教材中可挖掘的丰富资源进行开发和利用,是新课程实施过程中教师所必须做到的,因此,笔者结合自己的实践与感想,浅要表达一下如何创造性地利用好教材.
树立创造意识
按照课程设置进行教学,自然是教师应该做到的,但深刻解读、理解教材并进行创造性的使用也是教师教育教学工作中的必要内容,这需要教师内化、加工教材内容并进行创造性的整合才能实现.
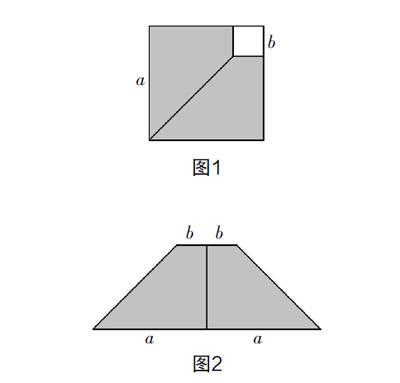
比如,平方差公式这一内容中的一个问题:已知边长分别为a和b的两个正方形,现将边长为b的小正方形置于大正方形上,如图1所示,计算可得未被遮住的部分的面积公式为(a+b)(a-b)=a2-b2. 教学中可以请学生自己动手进行拼图,并从多个角度对问题进行思考,学生就会寻得更多课本以外的解题办法. 如:
1. 可以将阴影部分的面积看成是两个梯形的面积之和,如图2,将两个小梯形拼成一个梯形,计算可得面积为 (2a+2b)(a-b)=(a+b)(a-b);
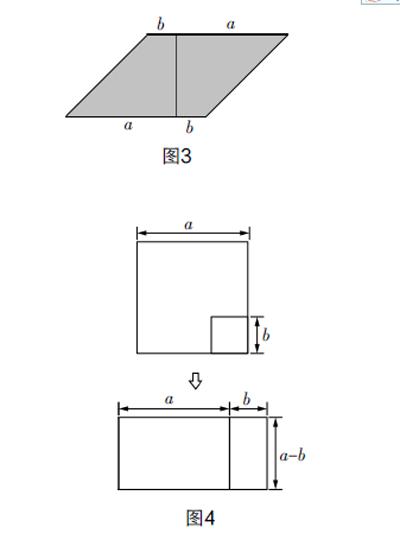
2. 将两个小梯形拼成平行四边形一样可以解题,如图3,其面积为(a+b)·(a-b);
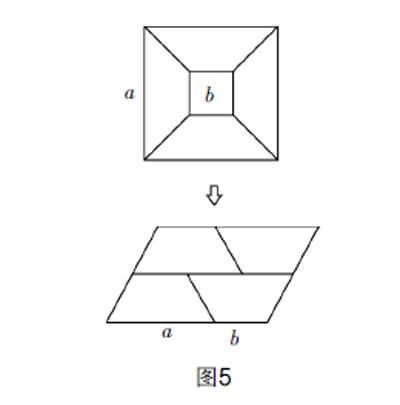
3. 既然是(a+b)(a-b),可否将(a+b)视作矩形的长,将(a-b)视作矩形的宽呢?如此,即可将余下的部分也剪拼成一个矩形,如图4所示,则其面积一样可以直接表达为(a+b)(a-b);
4. 在边长是a的大正方形中间剪去一个边长是b的小正方形,接着再把剩下的部分裁成四个相同的等腰梯形并拼成一个平行四边形,如图5,一样可得验证平方差的公式(a+b)(a-b).
概念教学中的创造性体现
抽象的数与具体的物质实体之间所建立起来的联系,能帮助学生对数与物质实体之间的共同属性获得清晰的认知,也能使学生在数与具体物质实体分离的抽象过程中获得更好的数学学习体验与感受.
比如,正切这一概念引出过程中的问题设计:台阶的倾斜程度怎样才能得到清晰而明确的表达呢?学生在观察中很快获得了用角来表示台阶的倾斜程度这一方法,如图6(1),但怎样用BC和AC的比来表示台阶的倾斜程度呢?引导学生对这一问题进行思考,可以设计以下的引入:首先利用图6(1)(2)来引导学生对AB与DE哪个更陡进行比较,使学生对利用BC和AC的比表示台阶的倾斜程度这一方法获得感性认识与理解.
接着再请学生对 为定值进行说明,也就是说,假如一个锐角A的大小确定,则其一边上任意一点至另一边的距离与顶点A到垂足的距离之比是恒定不变的. 学生理解至此,再引出正切的概念也就水到渠成了.
学习方法上的创造性体现
学生自身拥有的经验对其成才也能起到巨大的作用,教师在数学系统知识的教学中应充分挖掘学生已有的生活经验与知识经验,并看到其优势、不足与欠缺,使学生在数学学习的独特地位与育人价值的引领下不断丰富、发展、提升自身的经验.
比如,学生在学习完全平方公式的过程中往往会将(a+b)2和a2+b2混淆,利用特殊值能够对其进行说明:设a=1,b=2,则(a+b)2=9,a2+b2=5,因此(a+b)2≠a2+b2.当然,这只是对知识的简单列举和理解,教师同时还应引导学生从乘法的意义上获得充分的理解:因为(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2,因此(a+b)2≠a2+b2.当学生在乘法的意义以及面积的理解上获得充分认知后,在运用完全平方公式(a±b)2=a2±2ab+b2时,也就不易产生错误了.
美国教育家奥苏贝尔对于新旧知识间的联系尤为看重,他认为新知识与旧知识之间建立起合理而本质的联系才是有意义学习的根本体现,因此,将新旧知识联系起来进行学习,对于数学学习来说是极为关键且重要的方法.
比如,前面所讨论的完全平方公式中,确定2ab项的符号和有理数的乘法法则一样,都是同号得正、异号得负. 比如(a+b)2,(-a-b)2中2ab前面的符号是正的,(a-b)2,(-a+b)2中2ab前面的符号是负的. 学生在这样的分析与解释下也就容易理解了.
解题中的创造性体现
变式练习这一课堂教学的重要形式是促进学生联想、探索、推理的有效手段,也是充分调动学生积极性的重要方式.
比如,线段的中点这一内容的教学中有如下问题:
已知:如图7,线段AB=4 cm,点O为线段AB的中点,点C、点D分别为AO和BO的中点,则CD长为多少?
教学中可以进行如下变式:
变式1 已知:线段AB=4 cm,点O为线段AB上一点,且AO=3 cm,点C、点D分别为AO和BO的中点,则CD长为多少?
变式2 将题目中的“AO=3 cm”改成“AO=2.5 cm”,其他條件不变,试求CD的长.
这两个变式得出后,首先引导学生模仿教师的分析进行思考和解题,接着引导学生根据这两个变式再进行有规律的探索并得到了变式3.
变式3 将题目中的点O变成线段AB上的任意一点,即AO的长未知,引导学生探索CD的长和AB的长之间的关系,可得CD= AB.
解决了“O为线段AB上一点”之后继续进行变式,可得以下变式:
变式4 已知点O为线段AB延长线上一点,点C、点D分别为AO和BO的中点,则CD= AB这一结论依旧成立吗?理由何在?学生在前面知识的铺垫与问题的思考后再面对变式3和变式4,已经显得从容了许多,因此,可以直接让学生自主分析、画图并解决变式3和变式4. 不仅如此,笔者以为,学生在今后的学习中遇到此类题目必然也能从容应对.
学生只有依赖教材这一知识、方法、技能的基本载体,才能完成更好的学习,才能在以教材为依据的学习活动中掌握必要的知识与技能,才能在不断提升数学能力的过程中获得一般发展. 学生的学习离不开充分的学习资源,教师深挖教材内涵并进行创造性的设计、改编与组合,往往能将更具价值的数学、更利于学生发展的数学活动展现在学生面前,使学生获得更加良好的数学教育,从而增长智慧与技能. 因此,教师一定要从多个角度对教材进行理解和创造,并且将新课程理念充分体现在教学设计与教学实施过程中,使学生获得更为广阔的视野、充分的学习资源、思维的启发,从而实现数学能力的提升.

