食饵具有阶段结构和非线性出生率的捕食-食饵系统全局稳定性研究
刘晓婉,李晓然,周 芳
(皖西学院 金融与数学学院,安徽 六安 237012)
种群动力学是理论生态学研究的主要内容之一, 它以人类、昆虫和动物为主要研究对象,应用微分方程和动力学方法建立数学模型来研究种群的发展变化规律。近年来,阶段结构种群模型的动力学行为研究引起了学者们的极大关注,见文[1]-[9]以及所引文献。
1 研究进展
Chen,Xie等学者在研究阶段结构捕食-食饵种群模型的持久性和绝灭性时[1],发现针对他们所考虑的系统,食饵种群的绝灭并不意味着捕食者种群的绝灭,这似乎有违常识,其后他们经过分析认为,可能所构建的模型中,隐含了捕食者有其他食物来源的假设,从而哪怕食饵种群绝灭了,捕食者种群照样可能持续生存;Chen,Xie等学者提出了具有阶段结构的May合作种群模型[2],他们研究表明随着引入阶段结构,系统可以绝灭,残存或者两个种群稳定共存的,而众所周知的,对阶段结构的May合作种群模型而言,两个种群是恒稳定共存的,这表明阶段结构是引起生态系统动力学行为复杂的本质原因之一,是使得种群灭绝的关键性因素之一。
我们关注到这样一个事实,所有文献[1]-[9]的作者对具有阶段结构的种群均假设其幼年的出生率是成比例于成年种群的数量的,这种线性化的假设能使得系统动力学行为容易分析,但这种假设经常情况下不一定会客观反映现实情形。文献[3]-[5]的作者认为一个更为符合实际的模型应该要考虑到非线性出生率,事实上,文献[3]提出了具有非线性生育率的单种群捕获模型,作者讨论了平衡点的局部稳定性,其后借助Dulac判别法,得到了正平衡点全局稳定的充分性条件;文献[5]提出了具有非线性生育率的三阶段单种群模型,讨论了模型的稳定性态;文献[4]认为现实生活中,单独生存的种群是非常少的,更为符合实际的模型应该要考虑到种间作用,因此,他们在文献[3]的基础上,提出如下食饵具有阶段结构和非线性出生率的捕食者-食饵模型:

(1)
其中x1(t),x2(t)分别为食饵种群的幼年种群和成年种群在t时刻的种群密度,y(t)表示捕食者种群在t时刻的种群密度,这里假设捕食者仅捕食幼年食饵种群。记b=d+δ,δ=c,则系统(1)可以改写为
有关系统(2)各个平衡点的稳定性,作者得到如下两个结果。
定理1


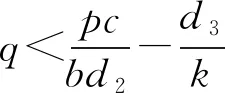
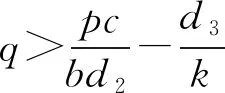
这里一些有趣的问题被提出:1)作者讨论了正平衡点的全局稳定性,但是作者未对系统的边界平衡点的全局稳定性进行探讨。人类对自然界的过度开发,越来越多的物种变成濒危物种,探讨物种的绝灭性成了非常重要的课题;2)作者在证明定理2时,借助了Dulac判别法,众所周知,Dulac判别法只能应用于二维平面系统,而对三维的系统,是不能直接应用的,因此,作者的证明是不严谨的,定理2的结论是否成立还有待探讨。
本文将对上述这两个问题给出肯定回答。我们主要是借助微分方程比较原理和通过构造适当的Lyapunov函数,给出保证系统的3个平衡点全局渐近稳定性的充分条件并给予证明,我们的方法具有一般性,可用于探讨相似的生态系统的稳定性问题。
2 主要结果
下面叙述本文的主要结果。
定理2.1考虑系统(2)


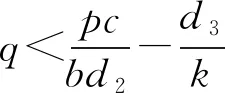
在给出定理的证明之前,我们需要如下引理,这是文献[3]中定理2的特例。
引理2.1考虑系统
(3)

下面给出定理2.1的证明。
(a) 由系统(2)的前两个方程和解的非负性,可得
今考虑系统
(4)
沿着系统(4)的正解计算V1(t)的导数,有

对系统(2)的任一正解(x1(t),x2(t),y(t)),不妨设其初值为
且令(u1(t),u2(t))是系统(4)的满足初值(u1(0),u2(0))=(x10,x20)的解,则由微分方程比较原理知当t≥0时,有xi(t)≤ui(t). 由系统(2)的解的正性,有
也就是有
(5)

由此知当t→+∞时,有
(6)
(5)和(6)表明系统(2)的边界平衡点O(0,0,0)是全局渐近稳定的。定理第一部分证明完毕。
(b) 由系统(2)的前两个方程和解的非负性,可得
今考虑系统
(7)
(8)
对系统(2)的任一正解(x1(t),x2(t),y(t)),不妨设其初值为
且令(u1(t),u2(t))是系统(7)的满足初值(u1(0),u2(0))=(x10,x20)的解,则由微分方程比较原理知当t≥0时,有
(9)
由系统(2)的解的正性及(8)和(9)可知有
(10)
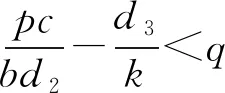
(11)
由(11)可知对足够小的正数ε1>0,有不等式
成立。也就是
(12)
成立。
由(10)可知存在足够大的T1>0使得对所有的t>T1有
从而当t>T1时,由系统(2)的第三个方程有
由此以及(13)可知:当t→+∞时,有
(13)

(14)
成立。对此ε2,由(13)知道存在足够大的T2>T1,使得当t>T2时
(15)
由(15)和系统(2)的前两个方程可知:当t>T2时,有
考虑系统
(16)
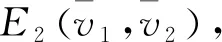
(17)
也即对系统(16)的任一正解(v1(t),v2(t)),有
(18)
对系统(2)的任一正解(x1(t),x2(t),y(t)),不妨设其初值为
且令(v1(t),v2(t))是系统(16)的满足初值(v1(0),v2(0))=(x10,x20)的解,则由微分方程比较原理知当t≥T2时,有
(19)
由系统(2)的解的正性及(18)和(19)可知有
(20)
由(10)和(20)可知有
(21)

(22)
(c) 我们将通过构造适当的Lyapunov函数来证明这一结论。今构造Lyapunov函数

(23)
沿着系统(2)的正解计算导数,借助(23)有
今取
则有
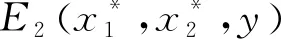
3 结论
黄任培提出了食饵具有非线性出生率的捕食者-食饵模型(1)[4],在将系数合并后,变成了系统(2),作者探讨了系统的各个平衡点的存在型,局部稳定性和正平衡点的全局稳定性。我们注意到作者有关正平衡点的全局稳定性的证明是不够严格的,Dulac定理并不能直接应用于三维系统,本文中,我们重新探讨系统(2)的3个平衡点的全局稳定性态。借助微分方程比较原理和通过构造适当的Lyapunov函数,我们获得了保证系统各个平衡点全局稳定性的充分性条件,对比定理1、定理2和定理2.1可知,保证系统(2)的各个平衡点局部稳定的条件就足以保证它们是全局稳定的。这样,我们就极大的改进和推广了文献[4]的主要结果。我们的方法具有一般性,可用于探讨类似的阶段结构生态系统。

