正切平方势量子阱的二次谐波

叶纯宝，李学超，张粮成，牛牧文

(安徽理工大学 力学与光电物理学院，安徽 淮南 232001)

近年来，由于低维半导体材料生长技术的快速发展，低维半导体材料的非线性光学性能受到了理论和实验物理的广泛关注，比如光吸收系数，折射率变化，光整流和二次谐波等[1-7]。这是因为相比于传统的体材料，低维的半导体材料拥有更好的非线性光学性能。良好的非线性光学性能对于研究光电器件的发展有一定的参考意义。

对于低维半导体材料的非线性光学性能，很多的研究者做了相关的工作。2015年，Shojaei研究了一个、两个以及三光子共振对于量子点折射率的影响[8]。研究结果发现：在共振情况下，折射率的变化很大程度上受到了量子点大小和光照强度的影响。2016年，袁研究了在电场的影响下，半抛物量子阱的二次谐波和光整流[9]。研究发现：随着电场的增加，二次谐波的峰值在不断的减小，光整流的峰值逐渐地增加，都向着低能量的区域移动。2017年，李研究了在电场作用下，三角形量子点的二次谐波和光整流[10]。研究结果表明：在外加电场的影响下，二次谐波和光整流的峰值都得到了很大的提高，并且在相同的位置取得了峰值。2018年，刘研究了量子线中的光吸收系数[11]。计算的结果发现：通过调节耦合状态可以有效地改变光吸收系数的峰值和位置。我们可以发现，二次谐波和光整流主要受到系统中的对称性的影响。

在本文中我们对正切平方势V0tan2(πz/L)量子阱中的二次谐波进行相应的讨论。在文中第二部分我们推导求解了正切平方势的能级与波函数以及二次谐波的表达式。第三部分引入相应的数值进行模拟和讨论。最后对本文作了一个简单的总结。

1 基本原理

在有效质量近似的条件下，系统的哈密顿量可以表示为[12]：

其中V(z)=V0tan2(πz/L)。表示普朗克常量，z表示量子点的生长方向，m*表示电子的有效质量，L和V0是限制势的参数，L表示限制势的宽度，V0表示限制势的高度。

通过求解系统的薛定谔方程我们可以得到系统的能级与波函数分别表示为：

其中n=0，1，2，3…，fn(t)分别表示为：

为了得到系统的二次谐波表达式，我们假设系统受到形如E(t)=E0cos(ωt)电磁场的激发。我们定义ρ作为密度矩阵，我们可以得到密度矩阵的运动方程为：

其中H0是没有电磁场的哈密顿量，ρ(0)表示无电场的密度矩阵，Γij表示弛豫率。我们利用迭代方法求解上式，可以得到[13]：

系统中电子的极化强度可以表示为：

其中，V表示相互作用的体积，Tr表示迹。因此我们可以得到二次谐波的表达式为[14,15]：

其中σv表示量子阱中电子密度，ωij=(Ei-Ej)/表示电子的转换频率，Mij=|〈ψi|z|ψj〉|表示非对角矩阵元。

2 分析与讨论

在计算正切平方势量子阱二次谐波的过程中，我们选用的参数如下：m*=0.067m0(m0表示自由电子的质量)，Γ=5×1012Hz，σv=5×1024m-3，ε0=8.85×10-12[16,17]。

图1为当限制势高度为40 meV，宽度分别为35 nm、40 nm、50 nm时，二次谐波随着入射光能量变化的曲线。从图中我们可以发现，随着限制势宽度L的不断增加，二次谐波的峰值逐渐的增加。并且在限制势宽度增加的过程中，二次谐波的曲线逐渐向着低能量的方向移动，出现了红移现象。从二次谐波的公式我们可以发现，二次谐波的峰值主要由矩阵元乘积|M01M12M20|决定的。为此，我们做出了矩阵元乘积与限制势宽度之间的变化曲线，如图2所示。从图2中我们可以发现，随着限制势宽度L的不断增加，矩阵元乘积不断地增加，这也表明二次谐波的峰值逐渐地增加。出现这种现象的物理解释是：随着限制势宽度的不断增加，不同的电子态逐渐地增加。

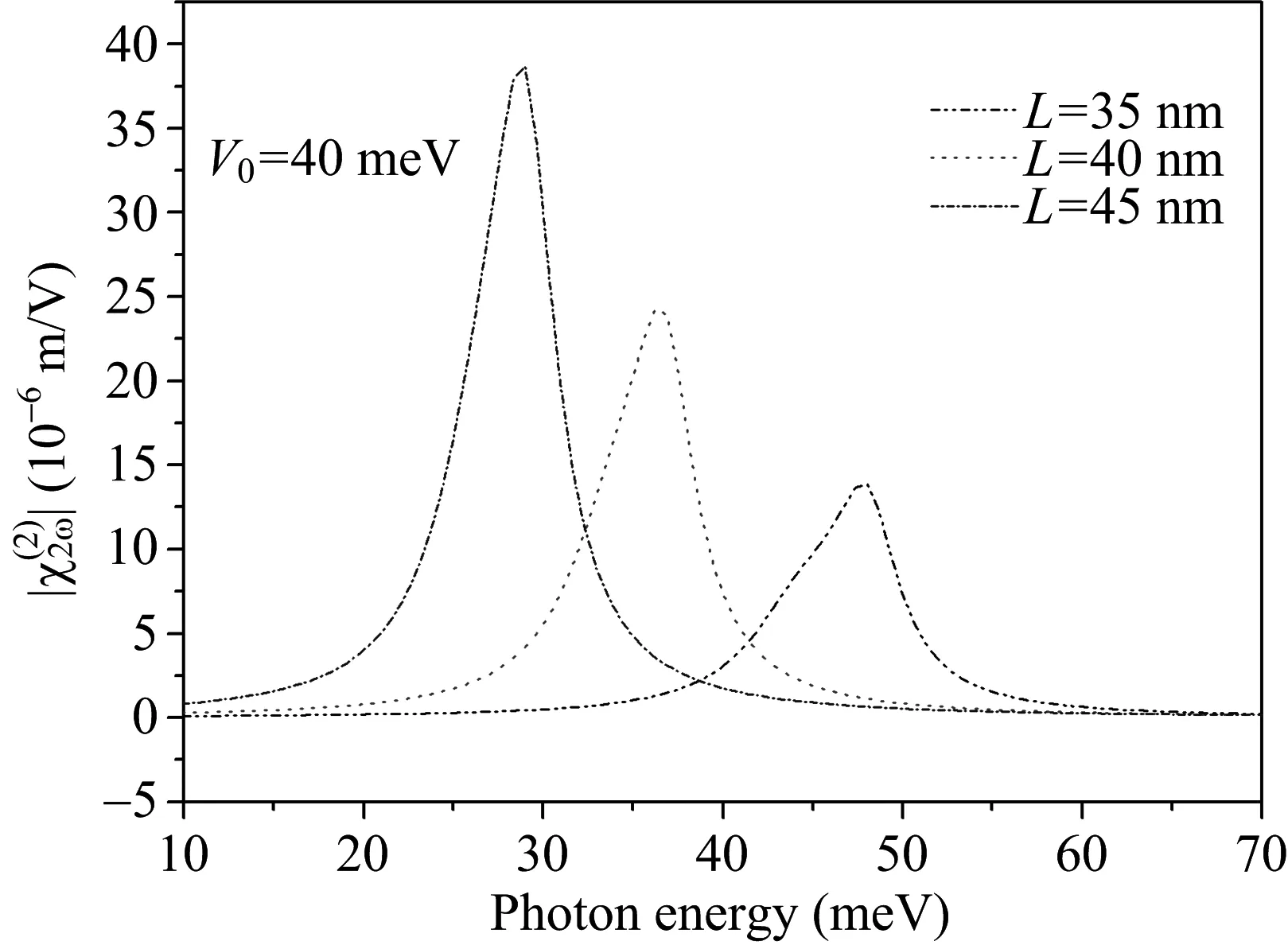
图1 对于不同的限制势宽度，二次谐波与入射光能量之间的变化关系

图2 矩阵元乘积与L之间的变化关系

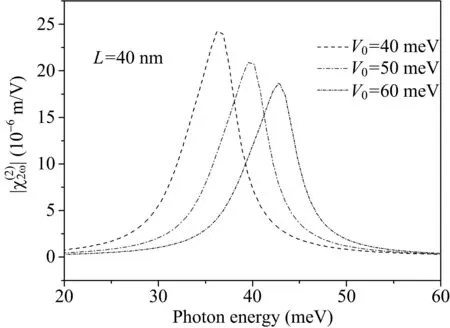
图3 对于不同的限制势高度，二次谐波与入射光能量之间的变化关系

图3给出了当限制势宽度为40 nm，高度分别为40 meV、50 meV、60 meV时，二次谐波随着入射光能量变化的曲线。从图中我们可以发现，随着限制势高度的不断增加，二次谐波的峰值逐渐减小，并且二次谐波的曲线逐渐地向着高能量的方向移动，出现了蓝移现象。为了进一步研究二次谐波峰值的变化原因，我们在图4中做出了矩阵元乘积与V0之间的变化关系。从图4中我们可以发现，随着限制势高度的增加，矩阵元乘积不断的减小，表明二次谐波的峰值逐渐的减小。

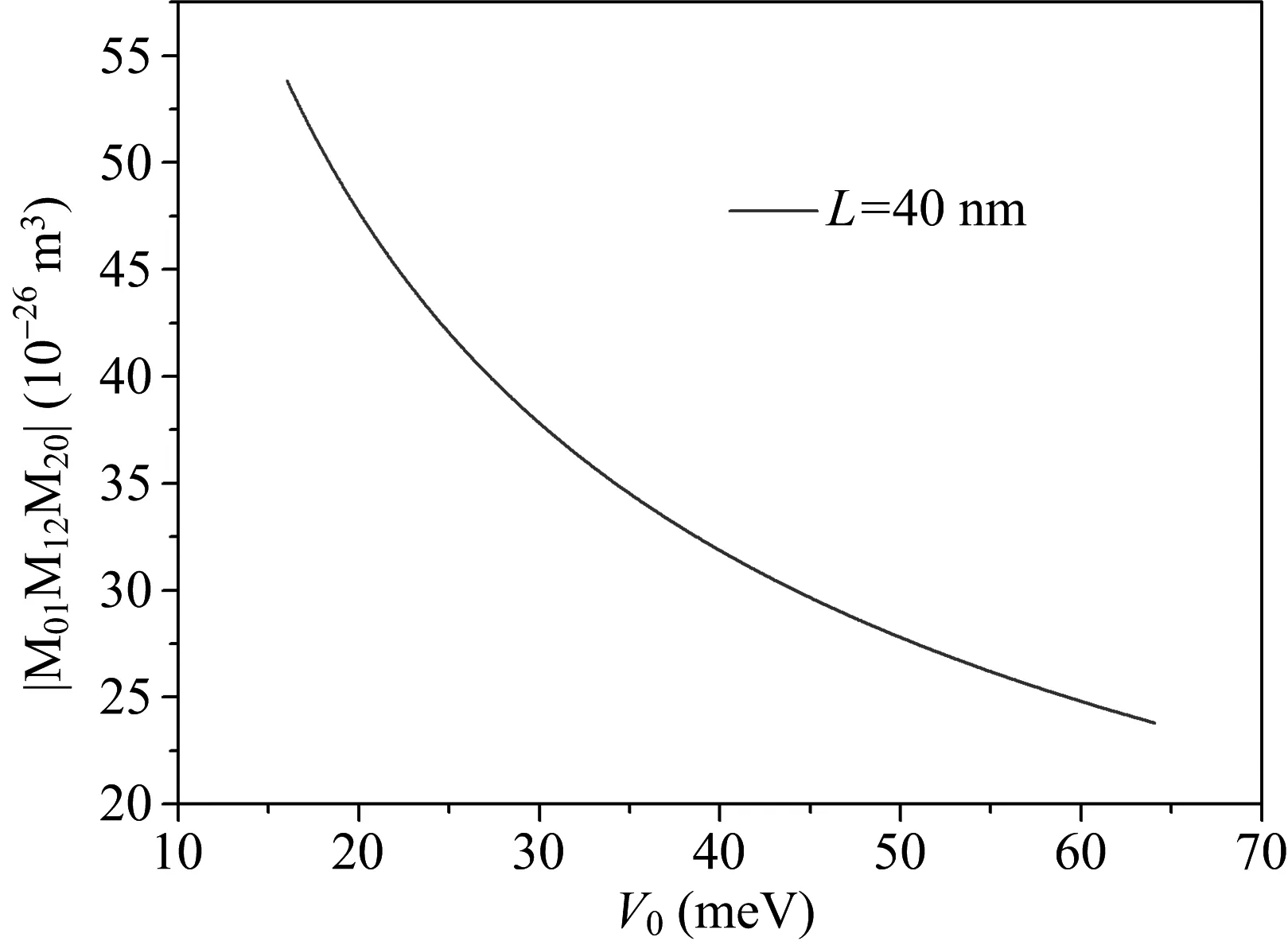
图4 矩阵元乘积与V0之间的变化关系

3 结论

本文主要研究了正切平方势中的限制势宽度以及高度对于二次谐波的影响。在我们的研究中可以发现，当限制势宽度L增加时，二次谐波的峰值逐渐的增加，并且向着低能量方向移动。对于限制势高度V0，当限制势高度V0增加时，二次谐波的峰值逐渐的减小，并向着高能量的方向移动，与限制势宽度L的变化呈现出了相反的变化。通过选取合适的限制势高度与宽度，我们可以获得恰当的二次谐波。