直觉模糊可退化的加权Bonferroni几何平均算子及其在多属性决策中的应用
李晓然,刘晓婉,岳 芹
(皖西学院 金融与数学学院,安徽 六安 237012)
随着社会的发展,人们在决策过程中遇到的对象越来越复杂,所面临的决策信息往往具有较大的模糊性和不确定性。在这种新形势下,为了更好地利用决策信息进行建模,学者们在模糊集理论基础上,提出了区间模糊集,type-2 模糊集,直觉模糊集等理论。由于直觉模糊集在实际决策中表现出的灵活性和有效性,使其倍受关注,相关理论也得到进一步的丰富和完善,并被广泛应用于工程技术、经济管理和军事等领域[1-4]。
集结算子作为信息融合的一种重要工具,一直是决策科学研究的热点。目前关于直觉模糊集的集结算子研究已取得丰硕成果,例如:文献[5]定义了直觉模糊加权平均(IFWA)算子以及直觉模糊有序加权平均(IFOWA:intuitionistic fuzzy ordered weighted averaging)算子,用于直觉模糊信息集结;文献[6]提出直觉模糊加权几何平均(IFWG)算子以及直觉模糊有序加权几何平均(IFOWG)算子,求解多属性决策问题;文献[7]给出直觉模糊连续有序加权几何平均(IFC-OWG)算子,用于解决直觉模糊和区间直觉模糊的决策问题;文献[8]定义了直觉模糊爱因斯坦Choquet平均(IFCAε)算子以及直觉模糊爱因斯坦Choquet几何平均(IFCGε)算子。
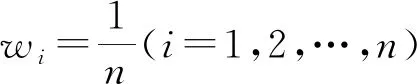
1 预备知识
1.1 直觉模糊集
定义1[1]设X是一给定论域,则X上的一个直觉模糊集A为
其中μA(x):X→[0,1]和υA(x):X→[0,1]分别代表A的隶属函数和非隶属函数,并且∀x∈X有0≤μA(x)+υA(x)≤1。
为便于讨论,将直觉模糊集中的元素用有序区间对α=(μα,υα)表示,并称为直觉模糊数。设αi=(μαi,υαi)(i=1,2),α=(μα,υα)是三个直觉模糊数,规定如下的运算法则:
1)α1⊕α2=(μα1+μα2-μα1μα2,υα1υα2);
2)α1⊗α2=(μα1μα2,υα1+υα2-υα1υα2);
现有的文献中较常见的一种直觉模糊数排序方式,是由徐泽水等人所定义,具体如下。
定义2[4]设α=(μα,υα)为直觉模糊数,称sα=μα-υα为α的得分函数,hα=μα+υα
为α的精度。设α1=(μα1,υα1)和α2=(μα2,υα2)为2个直觉模糊数,则有:
· 若sα1>sα2,则α1>α2;
· 若sα1=sα2,则
(ⅰ) 若hα1=hα2,则α1=α2;
(ⅱ) 若hα1>hα2,则α1>α2;
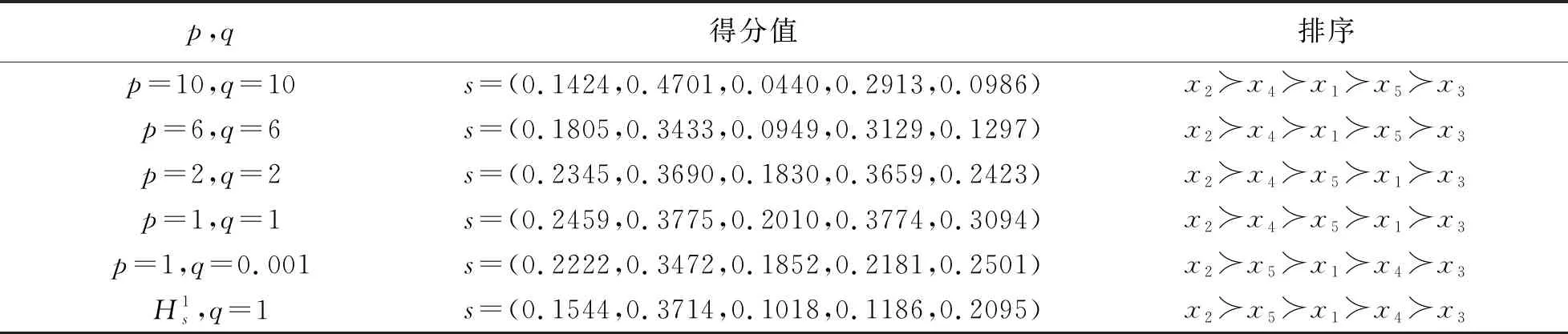
(ⅲ) 若hα1 定义3[9,10]设p,q,ai(i=1,2,…,n)为非负实数,若 则称Bp,q为Bonferroni平均算子, GBp,q为Bonferroni几何平均算子。 由于Bonferroni平均算子具有优良的性质,引起很多学者研究兴趣,尝试给出其加权形式,并推广到不同的模糊环境中。但这些加权算子都不具有退化性,为解决这一问题,Zhou给出如下的定义。 定义4[14]设p,q,ai(i=1,2,…,n)为非负实数,若 则称IWBp,q为可退化的加权Bonferroni平均算子。 定义5设p,q,ai(i=1,2,…,n)为非负实数,若 则称GBMp,q为Bonferroni几何平均算子。 易证GBMp,q满足下列性质: (1) GBMp,q(0,0,…,0)=0; (2) 若ai=a(i=1,2,…,n),则有GBMp,q(a,a,…,a)=a; (3) 若ai≥di(i=1,2,…,n),则有GBMp,q(a1,a2,…,an)≥GBMp,q(d1,d2,…,dn); 在定义5的基础上,可得如下具有退化性的加权Bonferroni几何平均算子。 则称IWGBMp,q为可退化的加权Bonferroni几何平均(IWGBM)算子。 下面将IWGBM算子引入直觉模糊环境中,并讨论其相关性质。 则称IFIWGBMp,q为直觉模糊可退化的加权Bonferroni几何平均(IFIWGBM)算子。 从而有 由此可得 因此有 下证,由IFIWGBM算子所得出的集结值是直觉模糊数。 显然有 又 综上,随着αi为直觉模糊数的变化,可得: 性质1(1)αi(i=1,2,…,n)为直觉模糊数,若α1=α2=…=αn=α,则有 (2)αi(i=1,2,…,n)为直觉模糊数,若α′1,α′2,…,α′n是α1,α2,…,αn的一个任意的排列,则有 (3)αi=(μαi,υαi),βi=(μβi,υβi)(i=1,2,…,n)为直觉模糊数,若μαi≤μβi,υαi≥υβi(i=1,2,…,n),则有 证明(1) (2) (3) 由μαi≤μβi,υαi≥υβi(i=1,2,…,n)可得 因此 类似可得 从而有 记直觉模糊元素IFIWGBMp,q(α1,α2,…,αn)和IFIWGBMp,q(β1,β2,…,βn)的得分函数为sα、sβ,精度为hα、hβ,则由上式可得sβ≥sα。 1) 若sβ>sα,则由定义2直接可得 2) 若sα=sβ,又μαi≤μβi,υαi≥υβi(i=1,2,…,n),因此 且 从而有hα=hβ,则由定义2可得 由1)和2)可得(3)成立。 (4)由(3)和(1)直接可得。 综上,性质1得证。 随着参数p,q的变化,我们可得IFIWGBM算子的一些特例。 情形1若q→0, 则有 称之为广义直觉模糊加权几何平均算子[6]。 情形2若p=1,q→0, 则有 称之为直觉模糊加权几何平均算子[6]。 情形3若p=2,q→0,则有 称为直觉模糊加权平方几何平均算子[3]。 情形4若p=1,q=1,则有 称为直觉模糊可退化的加权平方几何平均算子。 针对上述多属性决策问题,利用前文所定义的算子,给出如下的求解步骤。 步骤3利用方案xi的综合属性值αi,i=1,2,…,n,对决策方案进行排序并选择最优方案。 例1[15]某市打算建一个大型图书馆,经过研讨,决定从以下3个方面(对应的权重为w=(0.3,0.5,0.2)T),来对参与竞标的5个品牌空调厂商xi(i=1,2,…,5)进行排序。 图书馆建设管理委员会聘请评估专家对上述5家空调厂商进行测评,评估专家给出了如表1所示的直觉模糊决策矩阵。 表1 直觉模糊决策矩阵 下面用本文的决策方法,为空调供应商进行排序。 步骤1本题涉及的3个属性都是效益型指标,因此不需要进行规范化。 步骤2利用IFIWGBM集结算子对候选方案的综合属性值进行集结,结果如表2所示。 表2 IFIWGBM算子集结结果 步骤3利用方案xi的综合属性值对决策方案进行排序(如表3所示),并选择最优方案。 从表3可见对于上述决策问题,在不同的p,q取值下,尽管都一致认为x2厂商的空调是最佳选择,但空调厂商的排序不全相同。这意味着IFIWGBM算子给出的排序方案依赖于p,q的取值。前面我们已经讨论了当参数趋于0时,IFIWGBM算子可退化为直觉加权几何平均算子等形式,但这些算子没有考虑变量和余下变量整体间的关联性,无法体现Bonferroni算子的主要优势。同时考虑到计算复杂性的因素,建议在决策时取p=q=1。 下面我们将本文方法同已有的直觉模糊多属性决策方法进行对比,这里我们有代表性的选取:基于直觉模糊加权Bonferroni平均(IFWBM)算子的决策方法[15]、基于直觉模糊加权Bonferroni几何平均(IFWGBM)算子的决策方法[10]、基于直觉模糊优化加权Bonferroni几何平均(IFOWGBM)算子的决策方法[11]进行对比,具体结果如表4所示。 表3 排序结果 表4 方法比对结果 由表4可知四种方法主要区别在于决策途径,即采用的集结算子不同。文献[15]所使用的Bonferroni平均算子,主要依据算术平均设计,而其他三种算子是几何平均。文献[10]采用的算子仅考虑变量间的关联性,文献[11]则在文献[10]的基础上进行改进,进一步考虑了变量和余下变量整体间的关联性。但文献[10]和[11]在权重相等时无法退化为GB算子。本文方法综合考虑了变量间的相关性以及变量和余下变量整体间的相关性,同时在权重相等时可退化为“原形”——GBM算子。由于不同的算子侧重点不同,导致得到的排序也可能不同。因此在决策中要依据实际需求,选择恰当的决策方法。 在可退化Bonferroni加权平均算子的启发下,本文对Bonferroni几何平均算子进行重新设计,在此基础上给出了可退化的加权Bonferroni几何平均算子,并将其推广至直觉模糊环境,提出了可退化的直觉模糊加权Bonferroni几何平均算子,探讨了其相关性质和特例。本文还给出了直觉模糊多属性决策方法,理论分析与仿真算例表明了方法的可行性和有效性。1.2 Bonferroni几何平均算子


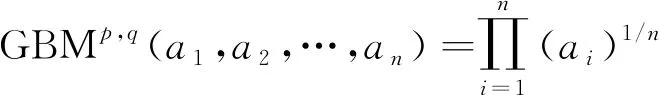

2 直觉模糊IWGBM算子


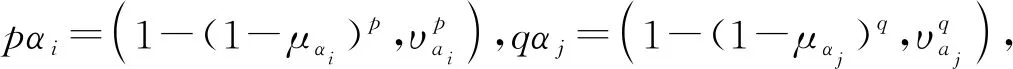
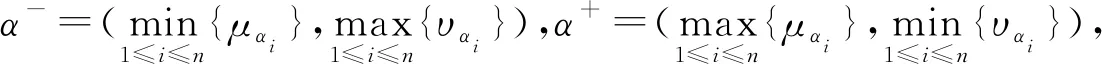
3 直觉模糊多属性决策方法



4 实例分析


5 比较分析

6 结论

