食饵具有非线性收获率的捕食系统的稳定性

冯 倩， 张 睿

(兰州交通大学 数理学院， 甘肃 兰州 730070)

0 引言

十九世纪二十年代，美国生态学家Lotka[1]和意大利数学家Volterra[2]提出了捕食者-食饵模型(Lotka-Volterra模型)，其形式为：

(1)

其中，x(t)和y(t)表示食饵和捕食者的种群密度，a表示食饵的内禀增长率，b表示捕食者掠食食饵的能力，c表示食饵对捕食者的供养能力，k表示捕食者的死亡率.

此后，国内外许多学者对系统(1)进行改进并作出了更加广泛的研究，其中收获率是影响种群系统的一个重要因素，学者们不但要考虑如何使生物资源尽可能大的满足人类生活需求，还要考虑怎么让生物种群保持可持续发展.因此，对具有收获率的捕食系统的研究是极其重要的.1981年Brauer等[3]研究了一类带有常数收获率的捕食者-食饵模型，讨论了平衡点和极限环的存在性.1986年，梁肇军[4]讨论了食饵种群具有常数收获率的Volterra模型：

(2)

其中，a10表示食饵的内禀增长率，a12表示捕食者掠食食饵的能力，a21表示食饵对捕食者的供养能力，a20表示捕食者的死亡率，a11和a22分别表示x和y的种内作用系数，h表示食饵的常数收获率.a10，a11，a12，a20，a21，a22均为正常数.文献[4]讨论了系统(2)平衡点的类型、平衡点的稳定性和极限环的存在性.

具有线性收获率的捕食系统也被学者们广泛关注，并作出进一步的研究[5-7].敬石心等[8]讨论了具有线性收获率和扩散因素的捕食者-食饵模型：

(3)

其中，b，b1，b2，a21，a12均大于零，E为捕获努力量，种群x1，x2在同一斑块Ⅰ中，y1种群限制在斑块Ⅱ中，x1种群可以在两个斑块间扩散，扩散率为D1，D2.文献[8]讨论了收获和扩散因素对系统(3)平衡点的影响，证明了此系统正平衡点的全局渐近稳定性.

由于人类对食物的捕获率是不断变化的，常数收获率显然不符合实际情况.而在某种情况下，线性收获率过大可能导致生态失衡，反之则不能促进经济发展，因此，具有非线性收获率的捕食系统引起越来越多的学者关注[9-10].文献[10]研究了带有非线性收获率和功能性反应的捕食者-食饵模型：

(4)

x(t)与y(t)分别表示食饵和捕食者的种群密度，r表示内禀增长率，K表示食饵种群环境容纳量，p表示被捕食率，q表示捕食者将捕获的食饵转化为自身增长的转化率,a1和a2表示捕捞能力，d表示捕食者种群的死亡率.M和N表示可以捕获的最大量,

为食饵和捕食者的非线性收获率.文献[10]讨论了具有非线性收获率时，系统(4)平衡点存在的条件、平衡点的局部稳定性和全局稳定性.

本文将文献[10]中的非线性收获率

引入模型(1)中，再考虑两种群的密度制约因素，讨论如下食饵种群具有非线性收获率的捕食者-食饵系统：

(5)

1 平衡点的存在性

可得到模型(5)的平衡点：

(1)平凡平衡点P1(0,0);

2 平衡点的稳定性分析

系统(5)在任意平衡点(x,y)处的Jacobian矩阵为

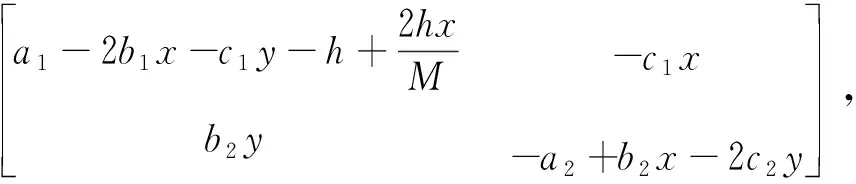
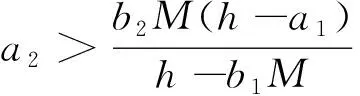
证明(1)将P1(0,0)代入J(x,y)中得到系统(5)在P1处的Jacobian矩阵为

其特征方程为

(λ-a1+h)(λ+a2)=0,

故特征根为

λ1=a1-h>0，λ2=-a2<0，

所以，P1(0,0)是鞍点.

其特征方程为

故特征根为

接下来考虑系统(5)的正平衡点P3(x*,y*)的稳定性.将P3(x*,y*)代入J(x,y)中得到系统(5)在P3处的Jacobian矩阵为

其特征方程为

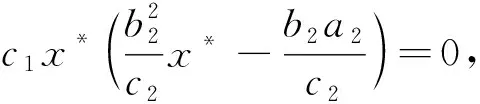
即

其中

令

T=b2x*-a2-s1x*-s2,

则特征方程可表示为

λ2+Tλ+D=0,

令

Δ=T2-4D,

由文献[10-13]可知下面的结论.

定理2(1)若D>0且Δ<0，则当T>0时，P3(x*,y*)为系统(5)稳定的焦点；当T<0时，P3(x*,y*)为系统(5)不稳定的焦点；

(2)若D>0且Δ>0，则当T>0时，P3(x*,y*)为系统(5)稳定的结点；当T<0时，P3(x*,y*)为系统(5)不稳定的结点；

(3)若D<0，则P3(x*,y*)为系统(5)的鞍点.

定理3若D>0，则当T>0时，平衡点P3全局渐近稳定.

证明取Dulac函数B(x,y)=xmyn，由于

g(x,y)=-a2y+b2xy-c2y2,

则

令

可得

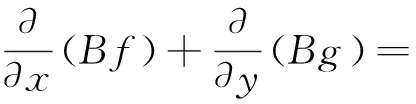
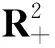
根据定理2和Dulac判据[14]得平衡点P3是全局渐近稳定的.证毕.

3 收获的调控作用

两个种群的平衡密度表达式为

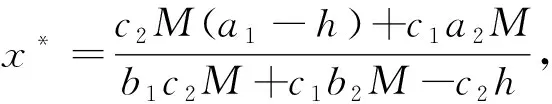
由

可以看出当食饵种群的捕获最大量M增加时，食饵种群的平衡密度随之减小，当食饵种群的捕获最大量M减小时，食饵种群的平衡密度则随之增大.由

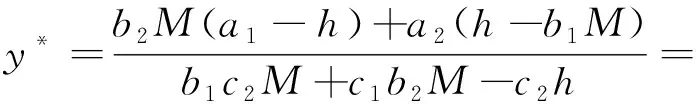
可以看出当食饵种群的捕获最大量M增加时，捕食者种群的平衡密度随之减小，当食饵种群的捕获最大量M减小时，捕食者种群的平衡密度则随之增大.

也就是说，由于人们的捕捞行为，食饵种群的捕获最大量M增加时，食饵种群密度随之减小，捕食种群所掠食的食物逐渐匮乏，其种群密度也随之减小.食饵种群的捕获最大量M减少时，食饵种群密度随之增大，捕食种群就有了充足的食物来源，其种群密度也随之增大.

4 数值模拟

这一部分主要运用MATLAB软件包对系统(5)正平衡点稳定的结(焦)点进行验证.对于系统(5)：

(1)如果a1=0.8，b1=0.05，c1=0.04，a2=0.03，b2=0.03，c2=0.07，M=2，则D=0.3959>0，Δ=-0.6405<0，T=0.9712>0.因此，由定理2(1)可知系统(5)的平衡点(18.2034，7.3729)是稳定的焦点，参看图1.

图1 系统(5)稳定的焦点

(2)如果a1=0.8，b1=0.05，c1=0.04，a2=0.01，b2=0.01，c2=0.07，M=2，则D=0.1784>0，Δ=0.0109>0，T=0.8512>0.因此，由定理2(2)可知系统(5)的平衡点(24.6047，3.3721)是稳定的结点，参看图2.

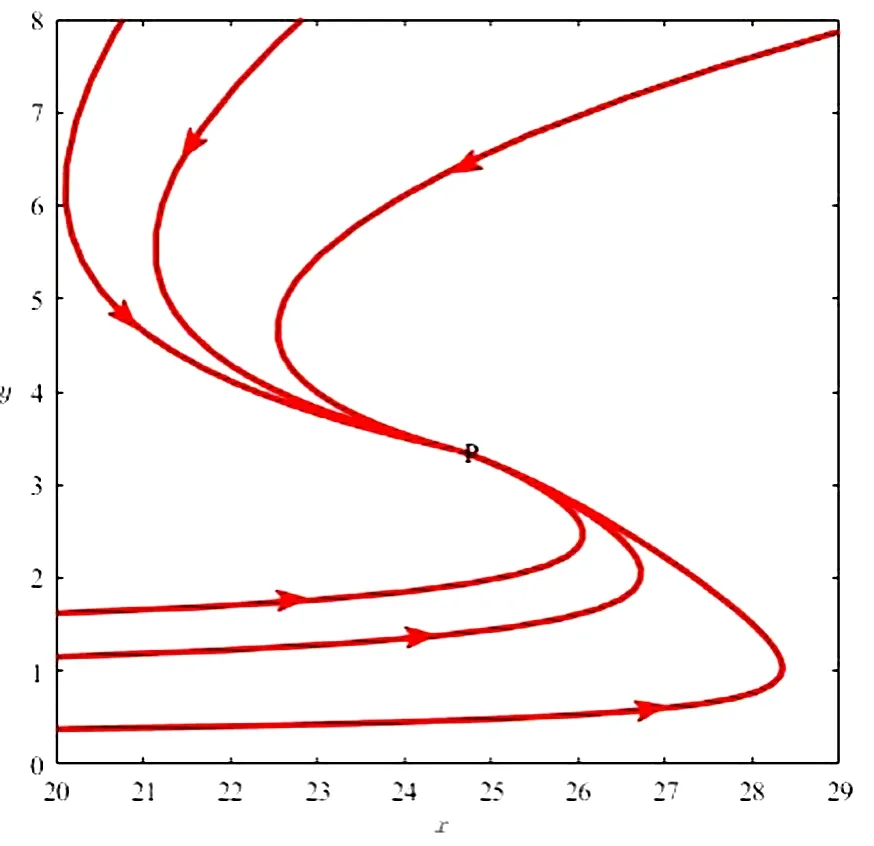
图2 系统(5)稳定的结点

5 结论

本文考虑一类食饵具有非线性收获率的捕食者-食饵模型，得到了系统平衡点的局部稳定和全局稳定的充分条件，说明了非线性收获率对这个系统的调控作用，并利用MATLAB软件对系统(5)正平衡点稳定的结(焦)点进行了数值模拟.