具有收获率和Holling-Ⅱ型功能反应函数的时滞系统的定性分析
沈 维, 姚佳佳
(兰州交通大学 数学系, 甘肃 兰州 730070)
0 引言
在生物数学中食饵-捕食模型作为重要的动力系统,近年来引起了许多研究者的广泛关注.在动力学研究中,稳定性与分支现象一直都是一个热点问题,从最初模型的建立到后来的广泛研究,数学家和生物学家致力于更准确地描述捕食者-食饵系统中存在的动态行为.为了体现捕食系统的复杂性与现实性,学者们还将功能反应函数引入系统中去.
2017年,Hu和Li[1]基于捕食模型
(1)
提出了以下具有时滞和Holling-Ⅱ型功能反应函数的捕食系统
(2)
其中变量和参数的实际意义见文献[1].他们主要研究了τj(j=1,2)的不同取值对正平衡点稳定性的影响.张宏民等[2]研究了以下具有收获率的Holling-Ⅱ类功能反应系统
(3)
其中F,G分别表示人们对食饵和捕食者的捕捞程度.他们主要对该常微系统进行了平衡点的稳定性分析.
2021年,Wang等[3]讨论了具有时滞和Holling-Ⅲ型功能反应的食饵-捕食系统
(4)

基于系统(2)和(3),本文将研究以下具有收获率的Holling-Ⅱ型功能反应的时滞食饵-捕食系统
(5)
通过详细分析系统(5)在正平衡点E*(u*,v*)线性化系统的特征方程来探究系统正平衡点的稳定性与Hopf分支.u,v分别表示食饵与捕食者的种群数量,参量意义参考文献[1,3].τ表示食饵的生产时滞.
1 无时滞系统的稳定性和Hopf分支
在τ=0时,系统(5)变为
(6)
由文献[1,4-5]可得以下结论:
引理1系统(6)的所有解都是非负的.


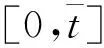
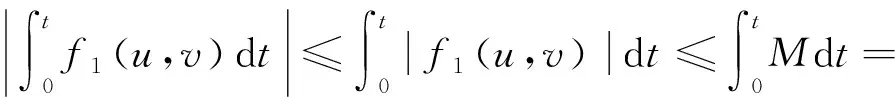
从而有
于是
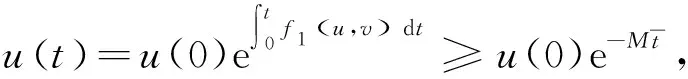
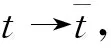

与假设矛盾,因此系统(6)的所有解都是非负的.
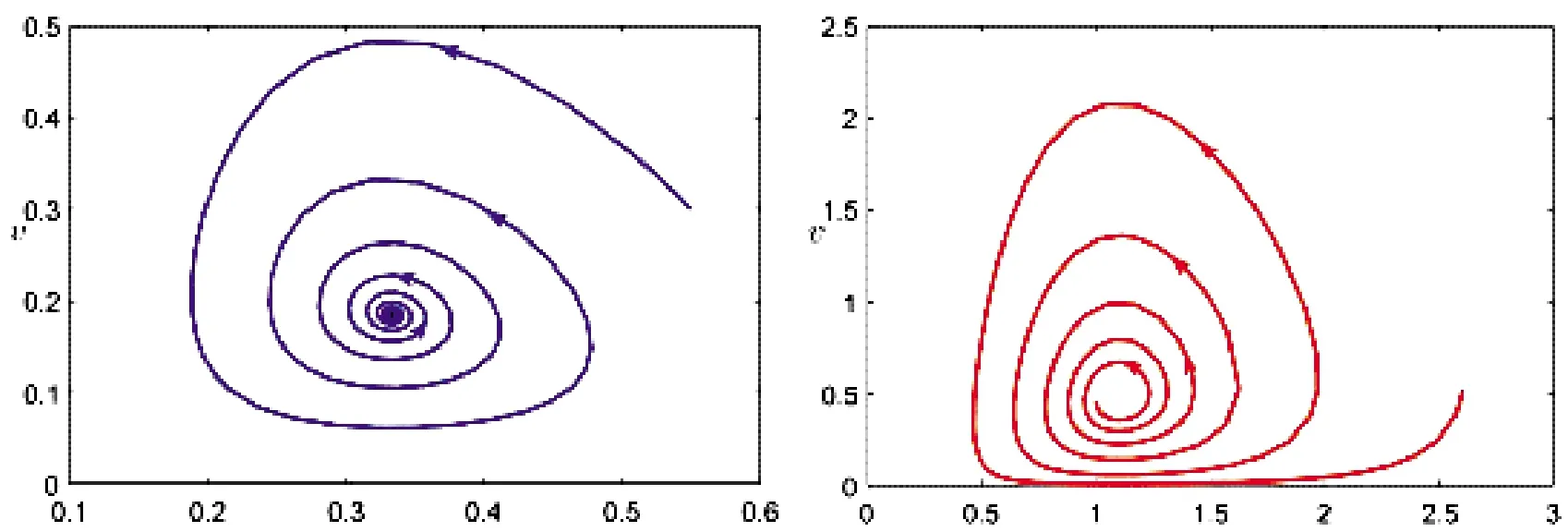
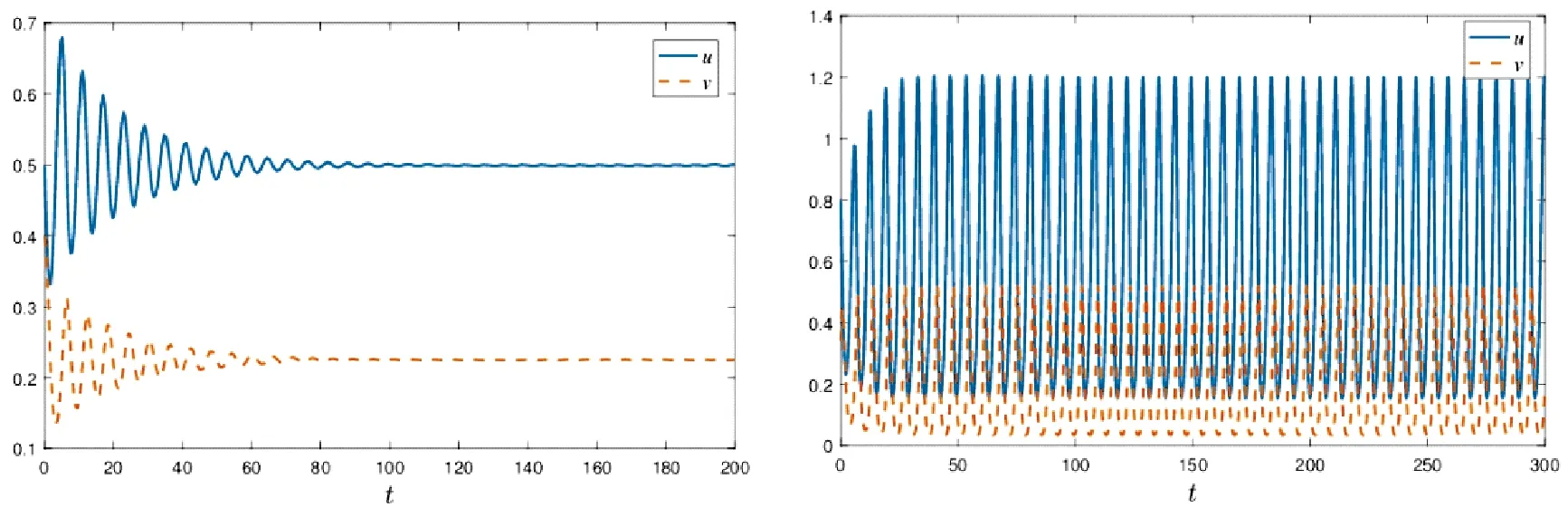
假设条件(B)1-F>0,βα>s+G且s+G 下面讨论常微系统(6)在平衡点的稳定性.在条件(B)成立下,系统(6)在某平衡点E(u,v)的线性化系统为 (7) 对应的系数行列式为 (8) 将E0(0,0),E1(K(1-F),0)分别代入系统(8)可得 由条件(B)和文献[3]知,系统(6)平衡点E0和E1是鞍点. 现将正平衡点E*(u*,v*)代入系统(7)得 (9) 线性系统(9)的特征方程为 其中 定理1(1)若Δ0<0,则当a11<0时,E*(u*,v*)为系统(6)稳定的焦点;当a11>0时,E*(u*,v*)为系统(6)不稳定的焦点; (2)若Δ0>0,则当a11<0时,E*(u*,v*)为系统(6)稳定的结点;当a11>0时,E*(u*,v*)为系统(6)不稳定的结点. (10) 在正平衡点E*(u*,v*)处对系统(10)线性化,得 (11) 其中 方程(11)的特征方程为 |λI-Γ1-Γ2e-λτ|=0, (12) 通过简单的计算,方程(12)改写为 λ2-(M+Ne-λτ)λ-PQ=0, (13) 其中 假设当τ>0时,方程(13)有一对纯虚根λ=±iω(ω>0),那么令λ=iω,则方程(13)变为 -ω2-iωM-iNωcosωτ-Nωsinωτ-PQ=0, (14) 分离方程(14)的实部和虚部可得 (15) 于是,ω满足以下方程 ω4+(M2-N2+2PQ)ω2+(PQ)2=0. (16) 令z=ω2,则方程(16)变为 h(z)=z2+(M2-N2+2PQ)z+(PQ)2=0. (17) 可得二次函数h(z)的判别式 Δ=(M2-N2+2PQ)2-4(PQ)2, 于是可得下面的结论: 引理2(1)如果Δ<0,那么方程(17)无正的实根; (2)如果Δ=0,那么当M2-N2+2PQ>0时,方程(17)无正的实根;当M2-N2+2PQ<0时,方程(17)只有一个正实根; (3)如果Δ>0,那么当M2-N2+2PQ>0时,方程(17)无正的实根;当M2-N2+2PQ<0时,方程(17)有两个正实根. 由文献[7-9]可知以下横截条件成立: 引理3假设z=ω2是方程h(z)=0的一个正根,则 假设λ(τ)=η(τ)±iω(τ)是方程(13)在τ=τj附近的一对共轭复根,那么对任意的j∈0,都有η(τj)=0,ω(τj)=ω+.因为h′(z+)=0,于是由引理3,以下横截条件 成立.于是,特征方程(13)的根没有正实部,由文献[10-11]知,此时系统(5)对任意的τ≥0,正平衡点E*都是局部渐近稳定的. 由引理2可得下面的结论: (i)Δ≤0; (ii)Δ>0且M2-N2+2PQ>0, 则对所有的τ≥0,系统(5)的正平衡点E*是局部渐近稳定的. 现假设条件(H) M2-N2+2PQ<0 成立,那么方程(17)存在两个正实根 则特征方程(16)也有两个正根 (18) 由方程(15)可得相应于ωk的τ的值为 (19) 由引理3可得 由文献[7]可得以下结论: 综上可得以下结论: 定理3假设引理4的条件成立,则 这一节主要借助于Matlab软件包进一步验证以上所获得的理论结果. 图1 系统(6)的相图 (a)τ=1.1 (b)τ=1.5图2 系统(5)的轨迹. 例2在时滞系统(5)中:取s=1,G=1,F=0.05,β=2,α=3,K=1,则a11<0,Δ>0且j0=1,于是可得: 即 0<1.2070<2.2135<7.1969< 13.1868<13.1982.





2 时滞微分系统的稳定性



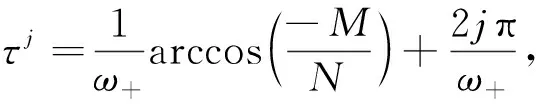


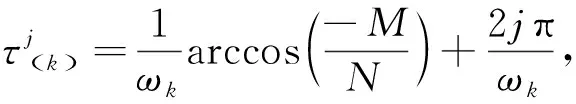
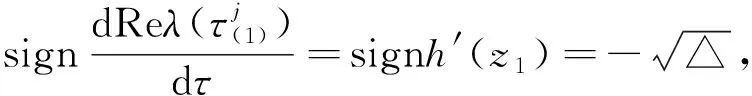
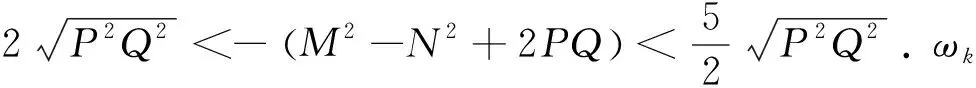
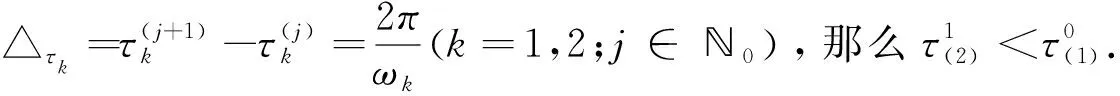

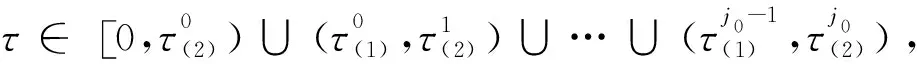

3 数值模拟