以“静”制“动”——初中数学中的动点问题分析

张小娟

(江苏省扬州市邗江区杨庙中学 225125)

一、动点问题归类分析

1.一条线段最值问题

(1)单动点问题

例题1 如图1所示，存在一个圆O，已经知道圆的半径为2.存在一条直线l，圆心到l的距离为3.假如在直线l上有动点P，PQ切圆O于Q点，则PQ的最小值是多少？

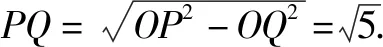
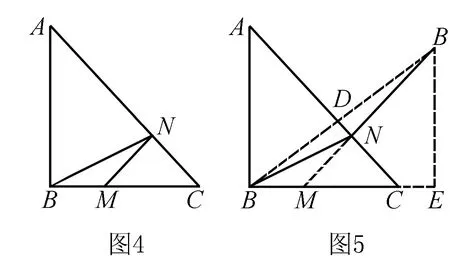
点评本题是一道单动点的一条线段最值问题，其难度不是太大，关键是学生能够根据勾股定理分析出决定PQ最小值的线段OP何时最小.

(2)双动点问题

例题2三角形△ABC三条边分别为AB、AC和BC，它们的长度分别为10、8和6，动圆经过C点，它和AB边相切，如图2所示.已知动圆与CA，CB相交于P、Q.请问PQ能够取得的最小值为多少？

解析AB、AC和BC长为10、8、6，满足勾股定理，△ABC是直角三角形，∠C=90°.∠C=90°可以说明线PQ为圆F的直径.假设点F是QP的中点，点D是圆F与线AB的切点.因为圆F和AB相切，有FD⊥AB.从图中可以看出，FC+FD=PQ.在三角形FCD中，FC+FD>CD.从图中可以看出，点F在△ABC高上时，CD能够取到最小值，PQ也为最小值.使用面积法，得CD=BC·AC/AB=4.8.因而，线段PQ的最小值是4.8.

点评本题是一道双动点的一条线段最值问题.因为问题以动态圆的形式出现，学生不易分析出线段PQ取最小值时的条件.在解决这道题时需要学生通过找圆心，绘制辅助线的方式来寻找突破口.

2.两条线段最值问题

(1)单动点问题

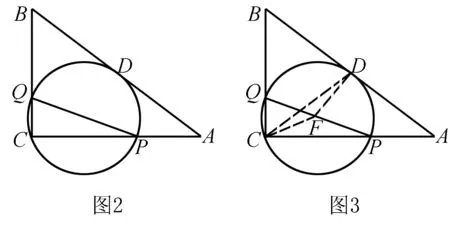
例题3有一个直角三角形ABC，边AB的长度和边BC的长度相等，都等于4，∠B=90°.M是直角边BC上的一个点.已经知道BM为1，N是AC上的动点.求BN和MN之和的最小值.

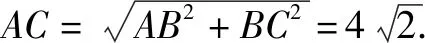
点评本题是一道单动点的两条线段的最值问题.在本题的解决过程中，使用到镜像法，这是一种比较难以掌握的几何技巧，需要学生对图形有一定的感觉.因为，学生在解题时要具有镜像法的应用基本能力.

(2)双动点问题

例题4矩形ABCD在一个平面直角坐标系中，如图6，矩形的顶点A、B、C的坐标是(0，0)、(20，0)、(20，10).线段AC上有动点M，AB上有动点N.当BM和MN和有最小值时，求点M的坐标.

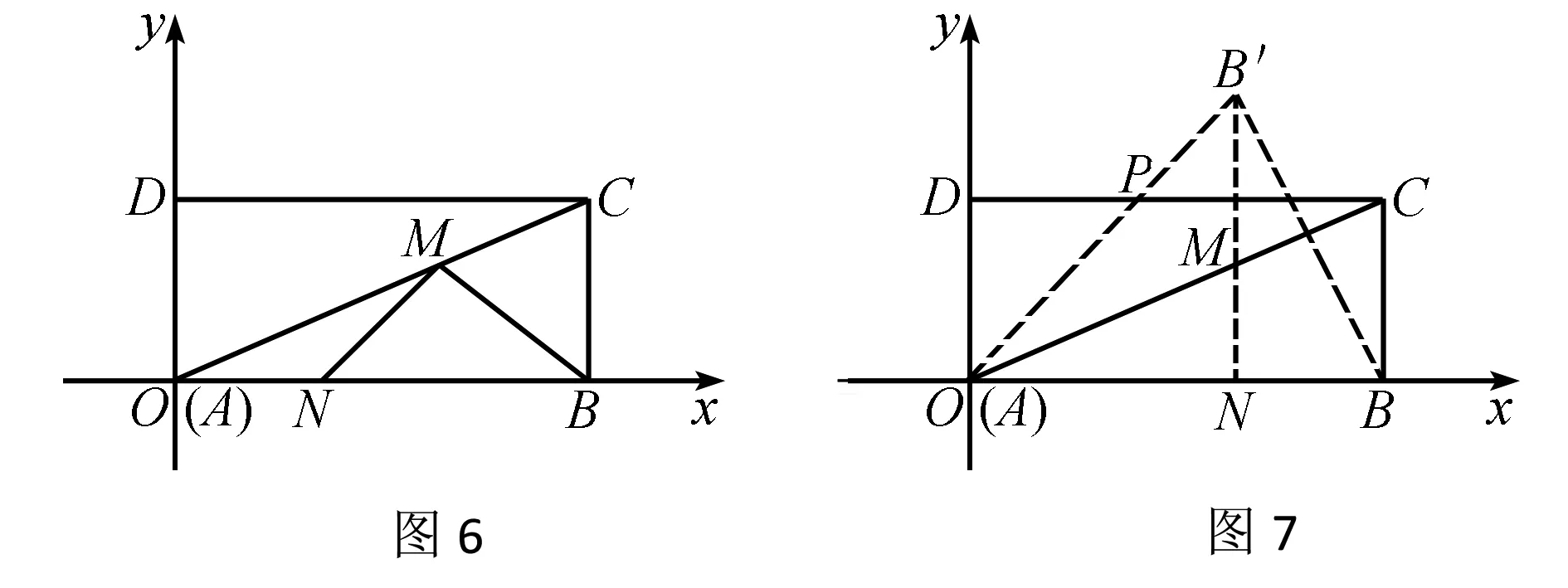
解析作点B关于AC的对称点B′，如图7.过点B′作OB的垂线，垂线B′N与MC相交于M点.从图中可以看出，B′N=B′M+MN，则B′N=BM+MN.BM+MN的最小值等于B′N的长度.将O点B′点连接起来，和DC交于P点.ABCD是一个矩形，则DC∥AB，有∠BAC=∠PCA.B和B’对称，所以∠PAC=∠BAC，则∠PAC=∠PCA，所以PA=PC.现在令PA=x，则PC=x，而PD=20-x.在直角三角形ADP中，有PA2=PD2+AD2，代入长度有x2=(20-x)2+102，解方程得x=12.5.因为cos∠B′ON=cos∠OPD，所以ON∶OB′=DP∶OP，有ON∶20=7.5∶12.5，则ON=12.因为tan∠MON=tan∠OCD，所以MN∶ON=OD∶CD，有MN∶12=10∶20，解得MN=6.因而点M的坐标是(12，6).

点评本题是一道双动点的两条线段的最值问题，具有较大的难度.在解题过程中，学生要采用镜像法画出B点关于AC的对称点，并使用勾股定理、三角函数、比例等方面的知识.

二、动点问题教学建议

1.强化基础教学

动点问题是一类综合性的问题，其涉及到初中数学中的几何变换、函数、比例、等数学知识.因而学生深入理解数学基础知识是解决动点问题的基础.在教学中，教师讲清楚数学知识的来龙去脉，并能够理解这些概念和规律的内涵和外延.在学生充分建构起对基本概念和规律的理解后，教师还要引导学生解决一定量的问题，以保证学生遇到不同问题时能够选择对应的解题方法.

2.开展针对训练

动点问题类型较多，每一个类型有其独特的解题方法.针对这个状况，教师可以将初中数学中经常出现的动点问题进行归类，并开设习题课分类讲解.教师在讲解动点问题时，可以让学生发现新的解题方法，并将仔细体会这些解题方法.在课外，教师可以布置一定量的作业让学生练习，以形成解题技巧的内化.