初中数学教学的定位思考和做法

吴 芳

(河北省石家庄市第九中学 050000)

十几年来一直从事初中数学的教育教学工作，对于初中数学知识体系的认识了解和多年的教学实践积累了一套自己的教学方法，形成了自己的教学风格.现做以下介绍，希望相互学习，取长补短.

我在教学中主要遵循三个一.一是：一个理念指导行动；二是：一个目标引领方向；三是：一条主线贯穿始终.

一个理念，就是结构教学的理念.结构教学即是整体构建和谐教学.所谓和谐教学就是按照系统论的观点在教学活动中，力求使教学过程诸要素之间以及教学过程与教学环境之间始终处于一种协调平衡状态，从而提高教学质量，促进学生的基本素质和个性品质得到全面和谐充分的发展.和谐教学不仅把教学过程看做一个系统，也把教学内容看作一个系统，要求学生在整体感知教材理解教材的过程中，尽快找到解决某类问题的方法和规律，做到举一反三，提高学习效率.我就是在这个理念的指导下挖掘教材，把握课堂，对待作业等一系列教育教学过程的.

一个目标，即培养学生的数学素质，提升应用数学解决问题的能力.先进的教育教学中功利色彩浓重，大量练习，有时是无价值的重复抄写，数学是理性的科学，不是重复记忆就可以解决根本性的问题的.我们数学教学不是教学生会做题是最终目的，而是让他们掌握这门科学工具.所以在数学教学中如何定位就是关键.所以我在教学中始终以培养学生运用数学的思想方法解决问题的能力作为根本目标.让学生懂得数学是源于生产生活，又应用于生产生活的一门科学，是我们研究其他科学的不可或缺的工具，让他们在数学知识的探究中领悟数学的精髓——数学思想，并学会运用数学思想方法解决问题，还能用数学语言表达自己的见解.

一条主线，即传授知识，渗透思想，提升能力.教育教学就是我们与学生交流的空间，是我们教数学知识经过加工处理呈现给学生的过程，用什么作为载体，辅以什么形式，怎样让学生易于接受，领悟其真谛，成为己能，这才是值得我深思的关键之处.数学教学的载体是数学题，首先从“一道题”开始，也是一个开端，就有了一种交流.

一、一道题

一道题拿到手，该从哪里入手解决才是正确途径的切入点呢？怎样才能快速解决呢？我以一道题为例：

如图，在正方形ABCD中，对角线AC上有一个动点P，∠MPN=90°，PM始终过点D，PN与BC交与点E，求证：PD=PE.

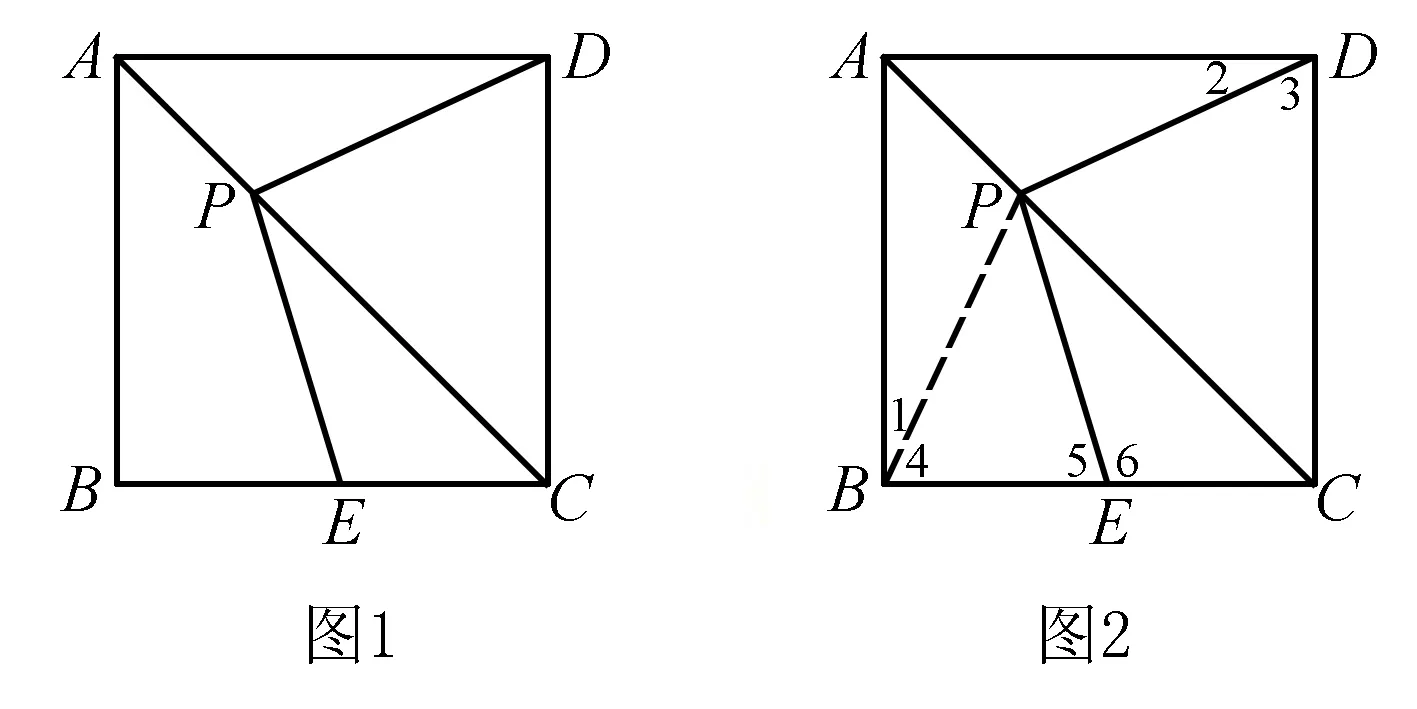
(1)教师引导学生完成分析问题，由第一个条件——四边形ABCD是正方形，你联想到什么？(学生想到对边相等且平行，四边相等，四个角为Rt∠，对角线互相平分，互相垂直且相等，每条对角线平分一组对角，还想到AC所在直线为正方形的对称轴)继续联想，如果连接PB，那么会有什么？(学生：△APB≌△APD，△BPC≌△DPC)从而可得PB=PD，那么还有∠1=∠2，继续，∠3=∠4，∠3+∠6=180°，∠5+∠6=180°，故∠3=∠5=∠4，所以PB=PE，则水到渠成地完成了证明.

这就是从已知出发，由学生联想，见一个已知，由其可得的所有结论联想出发，也就是对已知条件的充分挖掘，对图形充分认清，从而水到渠成地找到解决问题的方法和途径，即由因导果.这也就是我们数学方法中综合法的渗透.

(2)教师从未知需求出发，提出设问.要想证明线段相等，你希望有什么条件？(学生：全等，等角对等边，平行四边形，角平分线，中垂线等等)那么，没有全等，怎么办？(学生：构造)怎样构造？(学生：过P作FG∥AB交AD于F，交BC于G，如图3)此时，你希望什么？(学生：△PDF≌△EPG.现在有什么全等的条件？(学生：∠1=∠2，∠DFP=∠PGE=90°)你希望有什么？(学生：边相等)已知条件、已证条件和已作条件中有没有提供对应边相等的？(学生：有，AD=AB=FG，AF=FG，故DF=PG)，从而证出△DFP≌△PGE，PD=PE得证.

这就是从未知需求出发，寻求解决问题的“希望点”，即执果索因，顺藤摸瓜.其实质就是另一数学方法——分析法的渗透.当明确了我们所需求的条件时 ，我们就可以从已知出发寻找，也可以继续寻找下一个希望点，从而找到正确途径，所以综合法与分析法不是单一的运用，他们相辅相成，灵活应用效果更佳.

(3)一道题做完并不是我们最终的目的，关键是通过这道题我们要从中学会一种思想，一个方法，一个技巧，最终为那些数以万计的千变万化的题目都得以解决而积累经验和技能.所以，每道题目做完或讲完之后，师生要共同归纳总结这道题的收获，也就是提炼升华，反思解题技巧，感悟数学思想方法，实现由他知到己知的迁移过渡.

这一道题，不足以呈现数学这门科学的博大精深，更不能将数学的精髓——数学思想展现得淋漓尽致，这只是信手拈来的一道小题，只是进行说明的载体而已.

二、一个开端

对于每个人的第一个认知都是至关重要的，所以我们在教学过程中一定要把握好第一次，让学生在第一次接触之时就形成一个正确的、系统的认识，让其知识是完整的、科学的.所以，我对每课的开始尤为重视.

(1)由学生已有的纯知识系统来引入新课.例如，九年级三角函数的讲解，在认识上主要把握两个层面，一个是三角函数隶属于函数范畴，故引入时要由比例引入，从而展开讲解其函数特性，而故名为三角函数；另一个就是三角函数的求解是以Rt△为载体的，体现了Rt△中的边角关系.同时，将Rt△中的角角关系，边边关系统一成为一个完整的体系.

(2)由生活中的现象引入新知识，设置悬念激发兴趣.例如，讲圆这一章开始时，我设置了以下几个问题：我们在楼前楼后常见到下水道盖子，在家看到过洗手盆的下水口，为什么大多数是圆形的呢？为什么车轮采用圆形的而不是其他形状呢?一个立体的圆锥形帽子需要多大的纸张可以做成？等等.其中蕴含了什么数学知识？带着这些问题，我们开始新一章的学习.不仅激发学生的学习兴趣，而且，渗透了数学就在我们身边，只要我们善于发现，总能从中学到数学知识的思想意识.

(3)由已有的认知方式方法开始，类比式引入新课.例如，在讲矩形的性质这一节时，前面讲解了平行四边形的性质和判定，所以，利用平行四边形与矩形的关系，从角、边、对角线和对称性四个方面可以类比探究出矩形的性质，亦可区别出矩形的特性.矩形的特性也就是矩形判定方法的确立标准.此时，也给学生呈现了一种记忆方法和认识事物的途径.

三、一种交流

教学中教师是起主导作用的，而学生是主体，那么师生之间只有良好的交流才能让教学有秩序的呈良性循环，交流中有无声交流也有有声交流.我利用课堂上，对学生的问答来了解学生掌握的程度，交流思想.利用课堂中举手这一无声的交流手段，了解学生整体情况，做到控制局面，掌控进度.课下作业也是师生交流的媒体，作业的批改，不仅只有错对符号，还有错误原因、鼓励性语言，或是不同解法等等，从中传递着教育教学的点滴信息.所以有心人的作业本、练习册也是他学习历程的鉴证.所以，教学反馈是至关重要的环节，不容我们轻视.