试谈分类思想在初中数学解题中的应用

杜 薇

(江苏省徐州市少年儿童业余体育学校 221000)

一、分类讨论在函数问题中的应用

函数问题，是初中数学中的一个基本问题和重要问题，函数的知识点抽象且复杂，它通过不同的函数模型来描述因变量与自变量之间的变化关系，在问题处理上就更加复杂和麻烦.因而，教师在函数问题的具体解决上，可以适当地利用分类讨论思想帮助学生理解和学习.

如：已知函数y=ax2-(3a+1)x+2a+1(a为常数)，若该函数图象是开口向上的抛物线，与x轴相交于点A(x1,0),B(x2,0)两点，与y轴相交于点C，且x2-x1=2，并作点A关于y轴的对称点D，连接BC，DC，求sin∠DCB的值.

这个问题就是一道十分典型的函数类型的分类讨论问题.本题的关键在于，随着点A的移动，点B和点D的位置也随之而动，并导致∠DCB的变化.因此，本题的讨论标准在于讨论线段AB与x轴的相对位置，从而导致的x1(或x2)的值的变化.确定讨论标准，即x1分别在(-∞,-2)、[-2，-1)、[-1，0)、[0，+∞)等区间(见下图)，再分别利用二次函数和代数几何知识解决问题.

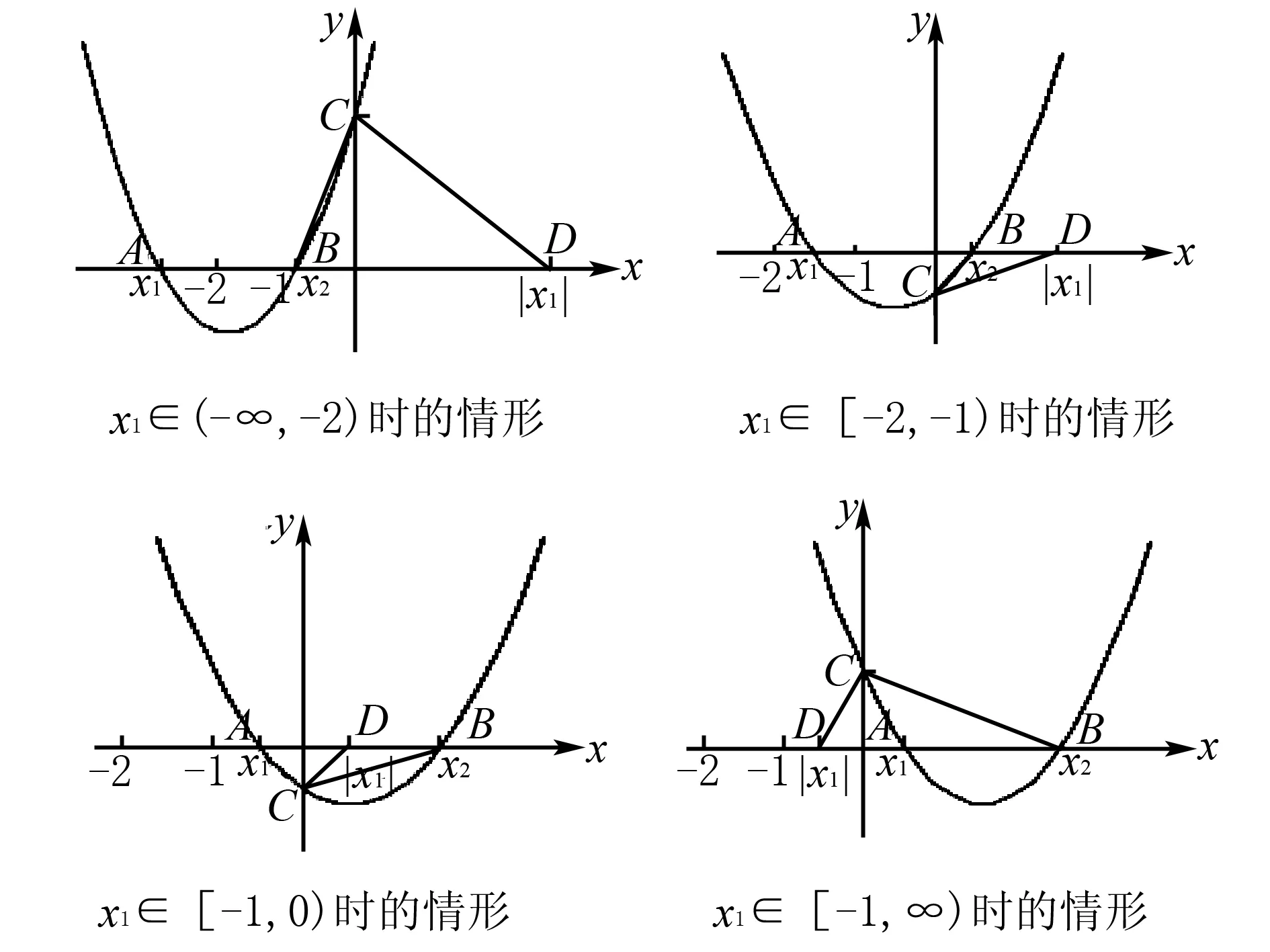
从这个例子可以看出，对于函数问题中的动点、动线段、动图问题，分类讨论是一种常规性和高效性的解决思路.教师在针对这一问题进行教学时，最主要的是找分类标准和逐个类别讨论两大问题.其中，分类标准往往是动图问题中的特殊情形，如这道题中的分类点均是∠DCB不存在时的特殊点;逐个类别讨论则十分考验学生的逻辑分析能力，只能通过充分的训练进行不断锻炼和提升.

二、分类讨论在代数问题中的基本应用

分类讨论在初中数学的代数问题中，也有着较为普遍的应用.这种应用，更多是由于代数问题中的某些固定性质所决定的，因而处理起来并不是十分困难，但考查学生对于代数问题的把握能力.

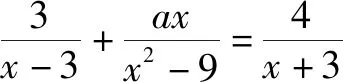
这个问题引发讨论的点在于，对该分式方程去分母化简后，得到的是为(a-1)x=-21的等式.那么首先需要进行考虑的是，该等式是否为一元一次方程，由此得出第一个标准是a=1，如果a=1，就不是方程了.其次需要讨论的是，该等式若为一元一次方程，分母不能是0，也就是x-3≠0、x+3≠0，而问题是无实数解，则说明x=3或者x=-3，这样，再分别讨论x是3、-3时，求出a的值，于是得出a的全部值为8，-6或1.

再如，已知方程m2x2+(2m+1)x+1=0有实数根，求m的取值范围.

本题引发讨论的点在于该方程是否为一元二次方程，由此得出分类标准m=0,继而分别讨论该方程作为一元一次方程和一元二次方程的情形下，m的取值范围.

这两道例题，足以引起我们对于代数问题中的分类讨论应用的注重，需要引导学生注意代数问题下的细节和性质，并熟练地将其应用到解题过程中.因此，教师应在这类问题上注重引导学生加强理解和把握，在分析问题的过程中领悟分类的本质内涵.

三、分类讨论在圆的问题中的基本应用

在初中数学中，圆相关问题向来是重点问题，其对于分类讨论的要求也最为严苛.学生在处理这类问题时，也往往难以理清思路，难以下手.但这类问题其实有着明确的解决思路和思维模板，因此，在这一问题中，尤其需要教师多多引导学生进行思考、分析和训练.

例如：已知两圆相交，且公共弦长为5cm，若两圆半径分别为3cm和4cm，那么圆心距是多少？

本题中，学生往往难以全面讨论，这主要是由于学生对圆与直线的位置关系难以把握所导致的.本题其实是圆心与弦的位置关系不唯一导致的分类讨论，因此依然可以看作是动图问题，当两圆心由远及近逐渐靠近时，存在公共弦为5cm的情况，从这一思路出发，不难发现该公共弦可能在两圆心同旁或之间，继而可以进行讨论解题.

再如，若圆O所在平面上一点P到圆O上的点的最大距离为a，最小距离为b，(a>b)，则此圆的半径为____.

对于这个问题，关键在于点与圆的位置关系不唯一，因此依然可以看作是动图问题，当P由远及近向圆心靠拢时，就分别出现了P在圆外和P在圆内两种情形，据此展开讨论分析，即可迅速解出答案.

总之，分类讨论作为初中数学的一大重点和难点，在初中数学解题中应用十分广泛和复杂.教师在帮助学生把握此类问题时，要善于利用“分类”思想，并引导学生了解和掌握分类思想在数学不同领域中的运用中的微妙的区别，真正掌握其使用方法和思维范式，从而帮助学生掌握好分类讨论思想，在具体问题中应用好分类讨论思想，以期最终能够深刻把握和熟练运用分类思想这一解题利器，提高数学解题能力，提高数学综合能力.