试论初中数学函数教学的有效方法

林锦辉

(福建省诏安县梅岭中学 363500)

一、运用数形结合思维方法，激发学生探索函数知识的热情

初中数学中的函数知识与其它文化类科目不同，它具有很强的思考性和探究性，如果教师一味地灌输函数理论知识，只会让学生失去学习的兴趣.而数形结合思维方法不仅有利于提升函数教学内容的生动性和直观性，也有助于激发学生的探索热情，让学生产生对函数知识的学习兴趣.所以，教师应该学会利用数形结合的思维方法，将抽象的函数概念运用数形结合的方式来讲授，才有可能提升课程教学的效率和质量.其中，数学教师必须先学会挖掘现有的教材内容，并利用数形结合的思想来展示有关的函数概念及表达式等，从而实现概念性内容向具体性内容的转化.

以二次函数解析式教学为例，学生可以利用二次函数图象示意图来获取解析式，也可以通过解析式来大体确定二次函数图象等信息，这些都应用了数形结合的思想教学方法，有利于帮助学生解决二次函数问题，从而提高学生的学习能力.比如例题：已知抛物线y=ax2+bx+c(a≠0)如图所示，请确定a、b、c、Δ的符号.

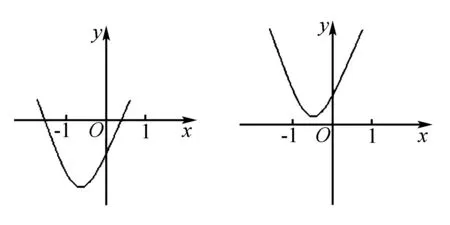
在上述这两道例题中，教师需要巧妙运用数形结合思想让学生去思考a、b、c、Δ与函数图象之间的关系，从而进一步得出a、b、c、Δ的符号，以此来锻炼学生的数形结合思维，使其养成良好的数形结合思想，这有助于学生日后的学习和探究.同时，数形结合教学思维模式也是学生解决函数问题的有效方法之一.所以，教师需要合理设置相关的函数练习题，从而针对性地锻炼学生应用数形结合思想的能力，促使学生掌握一定的数形结合思想，进而对问题展开针对性的解答.另外， 数形结合不单单是数字向图形的转化，也存在图形转化为数字的现象.这也要求教师注重培养学生的逆向思维，让学生学会合理利用数形结合思想.

二、注重化归思想的应用，以引导学生找到函数解题的思路

初中数学函数属于重点及难点内容，如果学生具备良好的数学思想，并懂得利用有效的思维模式，对问题进行一一的剖析，才有可能找到解题的突破口，从而快速地解答问题.然而，在实际解答函数问题中，很多学生往往拿到一道函数问题，没有经过仔细的思考和研究，就盲目地进行作答，不仅耗费了时间也增加了错误率.那么如何将函数问题简单化，引导学生运用正确的思路去思考问题，仍然需要教师采用合理的教学方法，培养学生具备良好的数学思想，才能有效地提高解题的效率和质量.

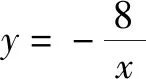
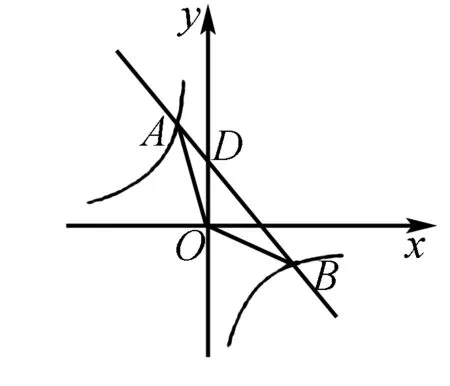
从题目中，我们可以看出两个函数的公共交点是A、B，而教师可以引导学生利用化归思维方法，将这两个函数转化为具体的方程，然后利用方程来解答问题，从而求出公共交点的坐标.如果学生不懂得应用化归思想去解决问题，势必会耗费很长的时间去解答题目，从而走入解题的死循环.所以，对于此类函数问题，教师可以运用化归思想，引导学生运用已经掌握的函数图象和性质去研究函数之间的关系，并建立相关的方程式，进而快速地解答函数问题.只有不断结合不同的函数问题，让学生们先回顾题目与所学知识之间是否有联系，以找到问题的性质及特点，使得学生懂得新旧知识的衔接，这样学生才能实现解题思路的化归转换，进而提高学生的学习效率.

三、灵活运用分类讨论教学法，巧妙开展函数课程教学

在初中数学教学中，除了教导学生上述两种数学思维方式之外，教师还必须注意培养学生的分类讨论思维，使其掌握和运用分类讨论方法去解答不同的函数问题，进而提升自身的分类讨论思维能力.教师想要掌握分类讨论解题法，就必须引导学生进行长期的课程问题训练，从不同的函数问题中总结思想方法的应用方式，才能真正掌握分类讨论解题法，从而有效地研究和解答数学问题.而教师可以结合比较典型的数学例题来进行分析和研究，让学生有效地抓住数学例题的根源问题，并结合分类讨论思想，对数学例题进行分类讨论，逐个击破数学问题，不断积累和总结思想方法的应用方式.那么教师该如何选取典型的数学问题，才能引导学生学习和掌握分类讨论思想方法呢？首先，教师可以从课本中的典型函数例题出发，结合函数的案例解析，深入理解和分析例题中所蕴含的分类讨论思想.

比如，在学习二次函数性质等内容时，学生会遇到许多关于函数图象性质的数学问题，这些问题需要学生利用分类思想来进行解答，才能有效地找出问题的答案.如下面这个问题：“y=x2-2x+8，求抛物线与x轴的交点个数.”因为Δ=b2-4ac>0时，抛物线与x轴有两个交点；当Δ=b2-4ac=0时，抛物线与x轴的交点个数变为1个.可见，上述这个数学问题包含了多种结果，所以教师需要引导学生对函数可能出现的结果进行分类讨论，从而利用分类思想方法解决函数的交点问题，这样有助于学生养成良好的分类讨论习惯.总之，在处理上述比较经典和常见的数学问题时，我们先学会理解问题所表达的意思，然后再运用分类讨论思想去思考问题可能存在的结果，并对可能存在的结果进行分类讨论，从而总结出有效的解题思路和途径.

综上所述，在开展初中数学教学中，教师需要具备良好的数学教学思维，并结合不同的函数问题，应用不同的数学思想来引导学生分析和研究函数问题，进而促使学生养成良好的数学思想习惯，最终让学生懂得利用有效的数学思维方法去解答函数问题，这样才能有效地提升函数教学的效率和质量.