初中统计与概率教学现状分析和建议

李璟璜

(福建省厦门市华中师范大学厦门海沧附属中学 361000)

一、初中教学统计与概率的教学案例现状分析

初中统计与概率分为三个部分，分别为七年级下册第十章数据的收集与整理，八年级下册第二十章数据的集中趋势，九年级上册第二十五章概率与统计.由于教材的编排位置都是在一本书最后一单元，加之我们前面所花费的课时，所以初中统计教学往往被压缩了极多的时间，教学参考安排的9课时往往让我们老师们用4到5课时就完成了整个单元的学习，造成了课时的缩短，把多出来的课时超前学习下一本书的学习内容，导致了我们对统计与概率部分，学生只会解题，没有让学生真正地去收集数据，整理数据，分析数据，缺少动手试验，从而未能从试验中得到活动经验.

例题(2017-2018学年(上)厦门市九年级质量检测)某市一家园林公司培育出新品种树苗，为考察这种树苗的移植成活率，公司进行了统计，结果如下表所示.

累计移植总数(棵)10050010002000500010000成活率0.9100.9680.9420.9560.9470.950

现该市实施绿化工程，需移植一批这种树苗，若这批树苗移植后要有28.5万棵成活，则需一次性移植多少棵树苗较为合适？请说明理由.

试题分析问题的提出是以人教版九年级上册第二十五章第三节问题1进行改编，本题最终是为了考查学生的对于频率与概率关系的知识掌握情况.对某种现象进行反复多次试验，经过多次的实验结果表明，现象发生的频率总在某一常数附近上下浮动，体现出了该现象事件发生的稳定性，选取频率稳定值为概率近似值，然后用样本估计总体.

本题的评分量表：

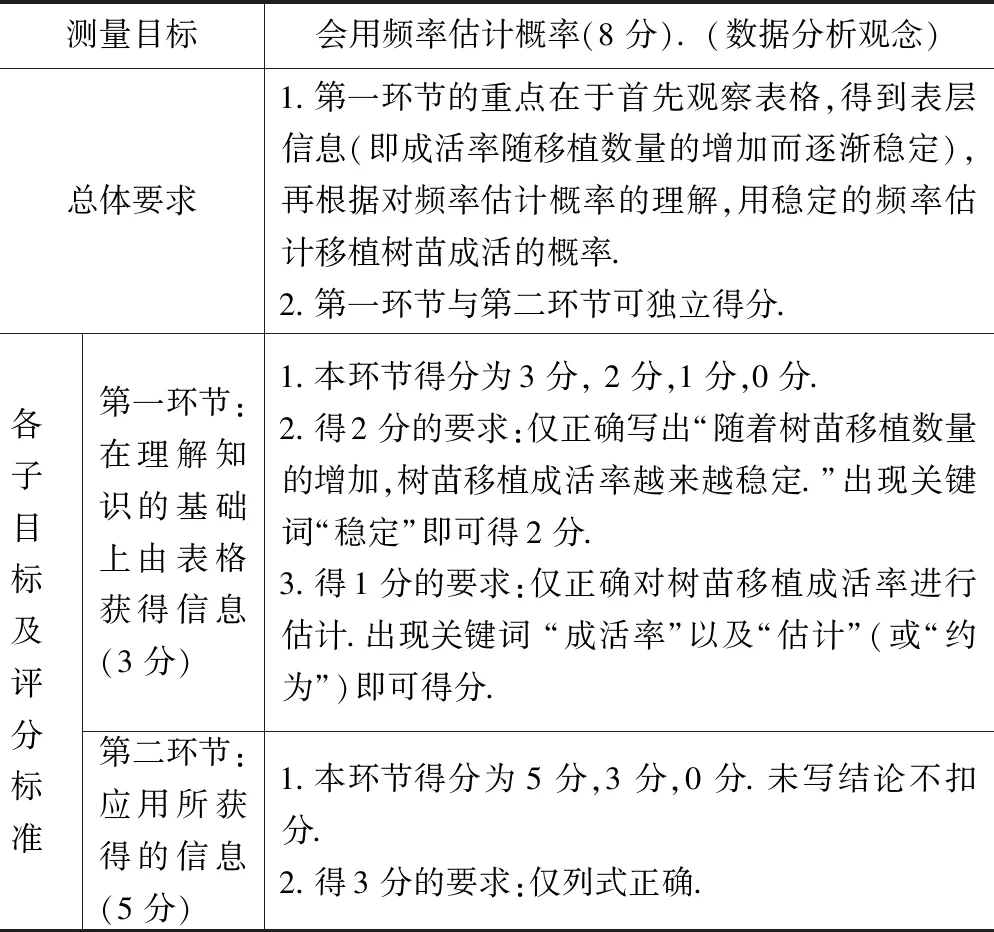
测量目标会用频率估计概率(8分).(数据分析观念)总体要求1.第一环节的重点在于首先观察表格,得到表层信息(即成活率随移植数量的增加而逐渐稳定),再根据对频率估计概率的理解,用稳定的频率估计移植树苗成活的概率.2.第一环节与第二环节可独立得分.各子目标及评分标准第一环节:在理解知识的基础上由表格获得信息(3分)1.本环节得分为3分,2分,1分,0分.2.得2分的要求:仅正确写出“随着树苗移植数量的增加,树苗移植成活率越来越稳定.”出现关键词“稳定”即可得2分.3.得1分的要求:仅正确对树苗移植成活率进行估计.出现关键词“成活率”以及“估计”(或“约为”)即可得分.第二环节:应用所获得的信息(5分)1.本环节得分为5分,3分,0分.未写结论不扣分.2.得3分的要求:仅列式正确.

答题情况分析：本题的难度值并不会太大，加之背景材料为课后练习，学生的审题应该不存在太大的问题，但是实测出来结果出乎所有人的意料.满分8分，全市均分仅有1.957分，还达不到25%，我们学校均分仅有1.6分，和25题的第一问所得到的均分相同，这暴露出学生对本知识的不理解.

错误的情况分析：

1.学生对题意理解错误，用频率估计概率的理解有误.

2.用平均数、中位数、众数作为成活率进行计算.

3.选择表格中成活率最高的数作为成活率进行计算.

4.概率统计的专业术语使用不到位，回答不到点上.

5.只给个答案，没有任何过程.

二、初中统计与概率的教学反思

教学应用的案例题目主要是利用频率与概率之间的关联性进行设问，有效解决该类型的问题关键节点则是需要了解什么阶段的频率可对概率进行估计，了解到只有在实验次数不断背景的下，让实验时间发生频率逐步稳定于某一常数附近时，选取该频率稳定值作为概率的近似值.需要注意的是在教学中要注重对本节的教学，课本用了三个例子来描述该现象，我们教学时候不能因为课时安排的原因而忽略了本节课的内容，很多学校对于本节课处理是用一节课描述频率约等于概率没让学生动手实践，做几个例题就完成了对这部分的学习，这是远远不够的.

本次课程教学的侧重点应在于需要对实验结果进行统计分析的基础上来研究概率问题.以抛硬币实验结果表明：抛硬币事件属于随机事件的一种，为此该事件不仅具备随机性，同时仍旧具备一定的统计规律.其统计规律性又体现于，抛硬币事件发生的次数与实验总次数的比值存在稳定性，即发生频率在某一常数附近摆动，这一频率稳定值也就被称为抛硬币事件的概率.其次，概率的题目较长，对学生的阅读能力要求很高，在教学中要重视引导学生的读题能力，审题能力，只有我们重视本部分内容，学生也才能更好地吸收知识.

三、初中统计与概率的教学建议

1.突出核心思想，把握重点和难点

这一学段的概率内容还处在一个比较初级的水平，教学重点是概率意义的理解和随机观念的培养.而随机观念的培养以及概率意义的理解是一个长期的过程，需贯穿统计与该流程的教学始终.教师在教学中要注意把握重点，控制难度.

2.充分了解学情，明确教学目标

学生具备一定的概率知识基础，为此教师在进行教学期间，需要以学生的实际情况进行教学设计，并不能仅依靠自身的主观意见进行盲目教学.同时教学时不能够盲目地压缩统计与概率的教学课时，过于的只练题目，而忽略了知识所存在的思想方法.尤其在进行新增的教学内容教学时，教师需要对学生进行全面调查，提升教学方式的针对性.

3.鼓励学生动手实验，注意现代信息技术的使用

统计规律性是需要通过不断进行发现的，采取以样本推断总体的形式来找出其中的概率，因此是实验科学.教师需要设计合理恰当的实验，直观认识其中的规律思想，在某些具体问题中，也可采取实验科学的方法来纠正发生错误判断的概率问题.

4.立足生活，凸显决策

统计概率案例大多是以生活实例为主题，展现其与学生生活息息相关的特征.基于此，需要适当选择学生生活周边较为典型的案例，让学生主动地寻求知识的实际背景，探索其应用价值.