一题一课：将探究引向深入

孙慧

摘 要：一题一课是通过对一道题探究，层层深入，剖析其内在关联和数理本质。本文以二次函数为例，铺设台阶，一题多变，引导学生进行科学有序的数学活动探究，实现数学思维的内化，促进学生反思、发散思维的完善。

关键词：一题一课;二次函数;数学思维

中学数学六大核心素养是教师追求的教学目标。而“勇于探究”和“勤于反思”如何才能内化为学生的能力？教学方式万变，不变的是教师的引导地位，学生能力的锤炼离不开教师的勤思考，勤探究。铺设学生够得着的台阶、引导学生搭建台阶、带领所有学生一起登台阶，是教学活动的难点所在。一题一课以二次函数为主线，通过探索二次函数图像中的几何问题，巩固二次函数的性质，体会数形结合、以形辅数、以数推形的巧妙关联。

1 情境引入

问题：

（1）请说出最简单的二次函数。

（2）试寻找与上述二次函数形状相同的其他二次函数，并写出其解析式。

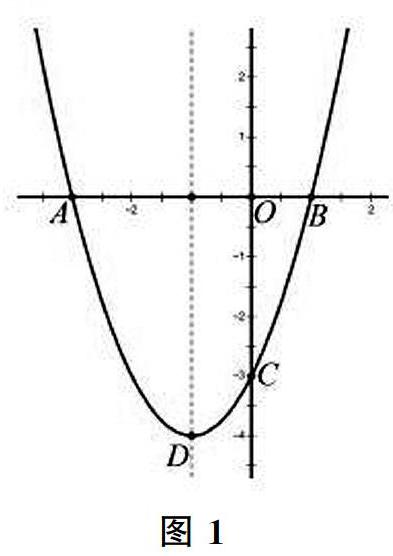
（3）将（1）中的函数向下平移4个单位长度，向左平移1个单位长度，得到新的抛物线，顶点坐标为点D，与纵轴交于点C，与横轴交于A、B点（A左B右）。试解释各点的几何意义。

教学预设：最简单的二次函数为y=x2，教师补充说明为何最简。第二题，学生对“形状相同”理解不充分，是脱离了对函数式中系数的认识，缺乏数形结合的思维锻炼。第三题，可能会有两点模糊点：为何要利用顶点式进行图像的平移？为何左加右减？以上问题回顾了二次函数图像基本性质，为后续拓展准备。

设计意图：让学生回顾二次函数解析式不同表示方法中的系数意义何在，体会数、形的相互依存。绘制如图1，供后续拓展准备。

2 拓展探究

活动1：在问题（3）的二次函数中，结合三角形的形状，你能在上述二次函数中提出什么问题？

教学预设：Rt三角形、等腰三角形，等腰直角三角形较为常见。以判断△ACD是否是直角三角形为例，可用勾股定理或斜率相乘为-1来处理。前者先用两点间距离公式表示线段长度，再用勾股逆定理判定其为直角三角形;后者利用一次函数斜率公式，K1·K2=-1，得到结论。对比两种计算方法，都离不开分类讨论，但计算量有差别。教师可总结提炼：倘若是探究等腰三角形，则一般是以线段长度公式和勾股逆定理为载体;倘若是等腰直角三角形，三垂图可为分析载体。

设计意图：让学生体验为自己出题，并在解题时对比不同方法的优劣，以及分类讨论思想及数形结合思想的价值。

活动2：结合三角形的面积，你能在上述二次函数中提出什么问题？

教学预设：学生多会提面积最值问题，或点的坐标。以下题为例：在AC下方的抛物线上，是否存在一个点N使△CAN的面积最大？求此時N点坐标。展示两种方法。

方法一：过点N作NM//y轴交AC于点M，S△CAN=1/2·MN·|XC-XA|=2/3·MN，面积最值转换为线段最值问题。

方法二：当△CAN面积最大时，过点N作直线l//AC，直线l与抛物线有且只有一个交点。联立l与抛物线y=-x+by=x2+2x-3，仅有一个交点，即△=0。

设计意图：动点问题，从设未知点着手。方法一将面积最值转化为线段最值问题，注意如何利用点的坐标正确表达线段长度。方法二从极限状态分析，即两个函数只有一个公共点，充分体现以形助数的优势。延续方法二，可追问点N到直线AC的距离是多少？

活动3：在抛物线上是否存在一点Q，使得Q点所在的三角形的面积等于△ABC的面积？

教学预设：学生在选取Q点所在的三角形时，较易想到去找另外两点为已知定点的三角形。以S△CAQ=S△ABC为例，点Q与点C到直线AC的距离相等，过点B作直线l//AC，交抛物线与点Q。联立直线和抛物线y=-x+1y=x2+2x-3，得到P1（-4，5）。

到此结束分析结束了吗？直线l在AC的上方，那么在AC的下方必然也会有一条直线m//AC，且到AC的距离与直线l到AC的距离相同，即m与l关于直线AC对称。那么直线m与抛物线是否存在交点呢？如图2所示。联立直线m与抛物线y=-x-7y=x2+2x-3，解得无实数根，即无交点。

设计意图：利用两平行线间的距离处处相等，将点的求解问题转换为一次函数与抛物线的位置关系问题，实现以形助数，同时考察如何分类如何讨论。

3 结语

数形结合是初中数学重要思想之一，然而对于很多学生而言更像一个口号，何时使用、如何使用却很模糊。在活动一对三角形形状的讨论，首先明确从哪些角度分类讨论，进而类比不同方法的优劣;活动二面积最值问题，可利用转化思想变为线段最值问题，或转化为一次函数与二次函数交于一点的几何问题;活动三继续精进，分类讨论两类函数在不同方向上的交点情况。通过本堂课半开放式的设问，引导学生从生硬数字向温婉图形过渡，面对纷繁的数学图形如何化繁为简、明确类型。数学思想的渗透还需锤炼。

参考文献

[1]吴立建.八年磨一课的思索与历程[J].数学教学，2015，（03）.

[2]夏乾冬.一题一课中渗透核心素养三步曲[J].中学数学教学参考（中旬），2019，（12）.