情境视角下的高考数学试题分析与思考

张景信 廖光及 林剑

摘 要：情境化的试题不仅能够考查学生的综合能力，更能够满足以素养为导向的考试要求.本文通过对2017-2019年全国高考数学理科Ⅰ卷进行统计与分析，探寻情境化试题的命题特点与不足，期望能够为今后的试题命制与高考备考提供借鉴与帮助.

关键词：情境化试题;核心素养;高考数学

伴随《中国学生发展核心素养》的提出，高考正在发生一场深刻的变革，从过去注重知识、智力、能力和技能的考查转变为考查学生的智力水平、思考深度、思维习惯和科学态度.情境化试题作为考查学生分析和解决实际问题能力的一种良好方式，能够有效渗透核心素养，考查学生分析问题、逻辑推理等能力，让学生在情境中思，在情境中解，在情境中感受数学的应用价值与魅力，将传统的数学解题转变为解决生活实际问题.以2017-2019年全国高考数学理科Ⅰ卷作为研究对象，对其中情境化试题进行统计与分析，并从试题情境、试题立意、考查功能等几个方面对典型例题进行研究分析，从中探寻情境化试题的命题特点与不足，期望能够为今后的试题命制与高考备考提供借鉴与帮助.

1 高考数学情境化试题的统计与分析

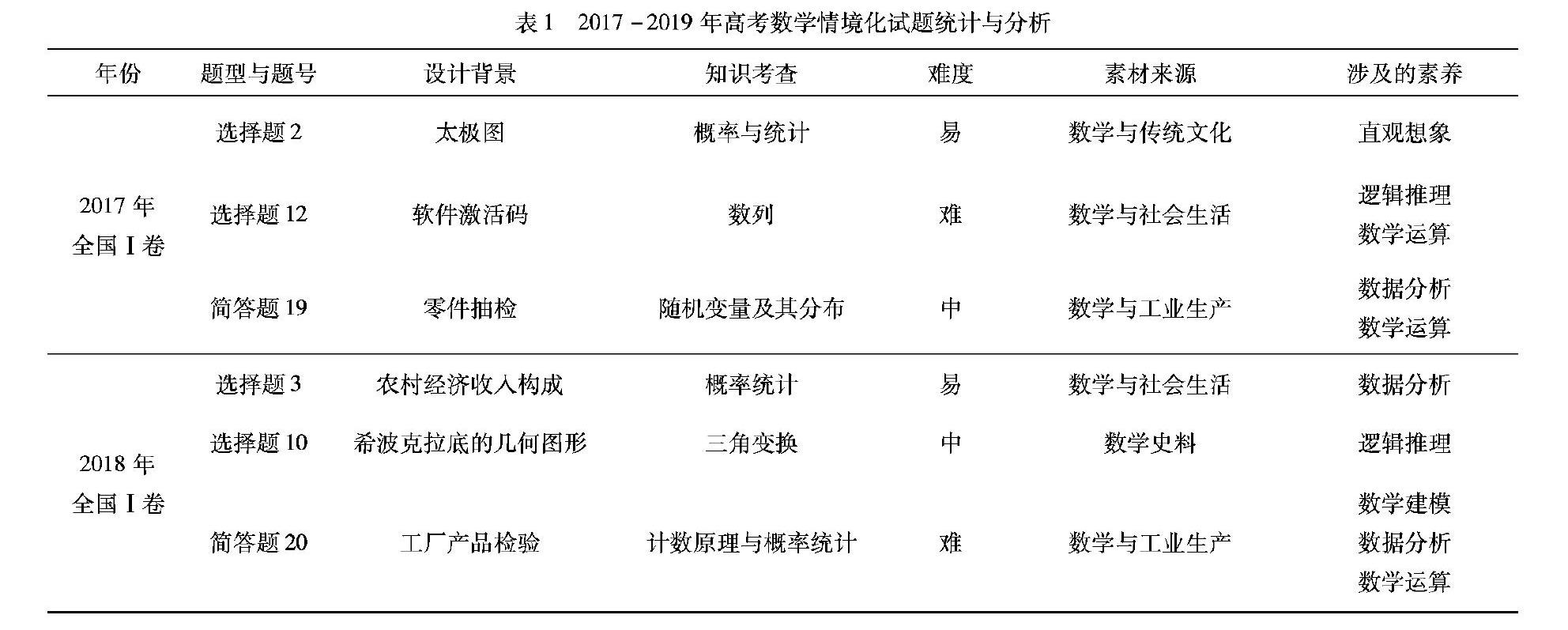
通过对2017-2019年高考数学试题的统计与分析，不难发现，情境化试题在每一年的命题当中都有呈现，并且在题量、分值占比以及题目难度上均有递增的趋势.从题型设置上看，选择题、填空题、简答题均有涉及，其中以选择题居多，并且每年都会出一道12分的简答题;从知识考查上看，情境化试题主要考查学生的概率统计相关知识，其余知识点涉及相对较少;从命题视角上看，该类型试题往往是以传统文化、社会生活和工业生产为背景，结合相关数学知识，进行情境化设计，情境涉及范围较为广泛;从试题立意上看，综合考查学生的问题分析、逻辑推理、问题解决和数学运算等能力以及数学运算、直观想象、数据分析、数学建模、逻辑推理等核心素养.

2 高考数学情境化试题的呈现与分析

2.1 以数学美学为背景的情境化试题

例1 （2019年全国理科Ⅰ卷第4题）根据古希腊时期人们对黄金分割的两种计算形式：人体头顶到肚脐的长度与肚脐到足底的长度之比和人体的头顶到咽喉的长度与咽喉到肚脐的长度之比均为5-12（约等于0618）.结合著名的“断臂维纳斯”雕像的实例，若某人满足以上两个比例，且其头顶到脖子下端长26cm，腿长105cm则其身高可能是（ ）.

A.165cm B.175cm C.185cm D.190cm

试题分析 黄金分割从数学的角度看是一种比例关系，但是从美学和艺术的角度去欣赏，往往能够产生一种美感，引起人们情感的共鸣.早在古希腊时期，人们就已经了解这个比例关系，并广泛应用于日常生活当中.该试题以古希腊著名雕塑“断臂维纳斯”作为案例，将黄金分割比例作为解题关键，引导学生建立数学模型：26x=0.618，26+xy=0618，从而求出结果为178cm.综合来看，该试题在考查学生建模素养的同时也考查了学生直观想象和运算素养，学生需要在脑海当中想象出人体的具体形象，以辅助建立模型，让学生真正感受到数学的魅力所在.在往年的高考试题当中，该类型的数学试题相对少见，命题角度较为新颖，但与其类似的数学知识并不罕见，比如斐波那契数列、心形曲线等，今后并不排除会以此作为命题背景对学生进行综合考查.

2.2 以传统文化为背景的情境化试题

例2 （2019年全国Ⅰ卷理科第6题）我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻位组成，而每个爻位为阳爻“——”或阴爻“— —”，如图2所示是一重卦，随机选取一个重卦中恰好有3个阳爻的概率是（ ）.

A.516B.1132C.2132D. 1116

试题分析 《周易》又称为“易经”，是我国传统经典之一，被誉为“群经之首，设教之书”，对我国传统思想文化中自然哲学和人文实践影响较为深远.该试题以周易中的卦象作为题设情境，引导学生运用组合的知识计算其恰好有3个阳爻的概率，通过计算可以得出其概率为P=C3626=2064=516，综合考查了学生的分析能力与数学运算能力，给予了学生一定的想象空间.通过往年的试题分析发现，高考数学当中常常会与传统文化、数学史料相结合进行情境化命题，譬如《九章算术》《天工开物》等，学生需要具备一定的阅读理解能力，从情境中提炼出数学问题，挖掘其中潜在的数学信息.

2.3 以社会生活为背景的情境化试题

例3 （2018年全国Ⅰ卷理科第3题）某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为了更好地了解该地区农村收入变化情况，统计了该地区新农村建设前后的经济收入构成比例，得到如图3，则下面结论中不正确的是（ ）.

A.新农村建设后，种植收入减少.

B.新农村建设后，其他收入增加了一倍以上.

C.新农村建设后，养殖收入增加了一倍.

C.新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半.

试题分析 党的十九大报告中提出 “乡村振兴”战略，该战略着重建设产业興旺、生态宜居、乡风文明、治理有效、生活富裕的新农村.经过一段时间的发展，部分农村取得了不错的成效.该试题以此为背景进行情境化命题，综合考查学生的数据分析素养，很好地体现了数学在生活中的应用价值.该类型的情境化试题是高考数学中的常见题型，往往以社会生活为背景，提供一系列的经济、消费等数据，考查学生对数据的分析能力.

2.4 以工业生产为背景的情境化试题

例4 （2019年全国Ⅰ卷理科第21题）为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种药更有效，为此进行动物试验，试验方案如下：每一轮选取两只白鼠对药效进行对比试验，对于两只白鼠，随机选一只施以甲药，另一只施以乙药，一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有放.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分;若都治愈或都未治愈则两种药均得0分，甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

（1）求X的分布列;

（2）若甲药、乙药在试验开始时都赋予4分;pi（i=0，1，…，8）表示“甲药累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1（i=1，2，…，7），其中a=P（x=-1），b=P（x=0），c=P（x=1）.假设α=05和β=08.

①证明：{pi+1-pi}（i=0，1，2，…，7）为等比数列;

②求p4，并根据p4的值解释这种试验方案的合理性.

试题分析 药效试验是帮助医生找到治疗某种疾病的方法，是病人安全服药的重要保障，同时也是医学药品在上市之前的重要一环，在医学界具有重要的意义与价值.本题以此作为背景形成一道分级设问的简答题.第一个设问相对简单明了，主要考查学生对分布列知识的记忆、理解和计算水平;第二问难度较大，需要考生利用数列知识建立数学模型，并求取p4的值，以此说明试验方案合理，实际上是考查学生的阅读理解、逻辑推理、数学运算等能力.将题设信息与已有知识相联系，从而解释试验方案的合理性.通过分析往年高考数学试题，我们不难发现，每年都会有一道同类型试题，但今年的试题阅读篇幅和题设难度均有所增加，对素养考查更加全面.

3 结论与思考

通过对近三年高考数学情境化试题的分析与研究，不难发现，近年来高考越来越重视对试题进行情境化创设.首先从素材来源的角度观察，无论是传统文化还是时事热点，无论是工艺美术还是文学作品均成为情境创设的素材来源，涉及范围广泛，呈现多元化发展;其次从试题立意角度观察，试题越来越注重对学生综合素养的考查，通过情境启发学生思考，激发学生的内在情感，锻炼学生的思维能力，增强学生的应用意识和创新能力，考查学生逻辑推理、数学建模等核心素养.因此，在数学教学中，应该注重学生阅读能力的培养，拓展学生的课外阅读，尽可能引导学生了解相关知识素材.在课堂教学以及习题训练中注重情境的创设，培养学生在情境中发现问题、提炼数学信息、运用数学的逻辑思维分析问题、解决问题的能力.

虽然当下的高考数学情境化试题存在着值得称赞的地方，但也存在着不足，这需要引起命题者的足够重视，对试题做进一步的优化与完善.首先是在知识考查方面，绝大多数情境化试题是在考查概率统计、数列等相关知识，而函数、几何等知识涉及相对较少，以2017-2019年全国Ⅰ卷理科高考数学试题为例，10道情境化的试题当中，有7道是考查概率统计相关知识.数学来源于生活，更应用于生活，任何数学知识都可以从情境化角度进行命题，考查学生的综合素养.因此建议命题者将更多的知识融入到情境化试题当中，凸显情境化试题的应用价值;其次是在情境设计方面，某些情境化的试题难以与考查内容实现真正的融合，存在着超出学生认知水平，冗余信息过长等现象，使情境的设计缺乏一定的合理性.以希波克拉底的几何图为例（2018年全国Ⅰ卷第10题），试题情境以几何图的形式呈现，学生对几何图无法做全面的了解，使情境化试题转化为常规试题，情境的价值难以得到呈现.因此，建议命题者加强对情境的创设与优化，让情境的设计能够符合学生的认知水平，让数学解题转变为解决问题.

参考文献：

[1]任子朝.从能力立意到素养导向[J].中学数学教学参考，2018（13）：1.

[2]中华人民共和国教育部.普通高中数学课程标准[M].北京：人民教育出版社，2017.

[3]罗文军，刘娟娟.2018年高考数学文化试题分析及教学建议[J].教育科学论坛，2019（08）：71-74.

[4]黄翔，李开慧.关于数学课程的情境化设计[J].课程·教材·教法，2006，26（09）：39-43.

[5]李开慧. 關于数学教学中情境设置有效性的思考[J].教学与管理，2010（22）：66-67.

（收稿日期：2019-11-06）