一道越南数学奥赛题的另证、推广与加强
黄锦涛 谢涛 叶济宇


摘 要:本文以一道2018年越南数学奥林匹克竞赛题为背景,给出了这道试题的另一种证法,接着给出了四元推广和加强并进行了证明,最后给出了n元推广和加强.
关键词:越南奥赛;推广;证明
1 試题呈现
试题 (2018年越南数学奥林匹克竞赛)已知a,b,c是满足ab+bc+ca=abc的正数,求证:b+ca2+c+ab2+a+bc2≥2.
2 试题解析
文[1]对这道竞赛题进行了证明,下面给出另外一种证明方法.
证明 因为(a-b)2≥0,所以(a+b)2≥4ab,a+b≥4aba+b=41a+1b.
同理b+c≥41b+1c,c+a≥41c+1a.
根据基本不等式可得
b+ca2=1a2(b+c)≥1a2·41b+1c=41a21b+1c.
同理有c+ab2≥41b21c+1a,a+bc2≥41c21a+1b.
所以b+ca2+c+ab2+a+bc2≥
4(1a21b+1c+1b21c+1a+1c21a+1b).
由权方和不等式得
1a21b+1c+1b21c+1a+1c21a+1b≥(1a+1b+1c)22(1a+1b+1c)
=12(1a+1b+1c).
再由ab+bc+ca=abc得1a+1b+1c=1.
所以b+ca2+c+ab2+a+bc2≥4×12=2.
3 试题推广
通过观察,可以发现这道题可以推广到四元,相应的题目如下:
推广1 已知a,b,c,d是满足abc+abd+acd+bcd=abcd的正数,求证:
b+c+da2+c+d+ab2+d+a+bc2+a+b+cd2≥3.
证明 由均值不等式有ba2+ba2+ab2≥3a,
ca2+ca2+ac2≥3a,
da2+da2+ad2≥3a;
cb2+cb2+bc2≥3b,
db2+db2+bd2≥3b,
ab2+ab2+ba2≥3b;
dc2+dc2+cd2≥3c,
ac2+ac2+ca2≥3c,
bc2+bc2+cb2≥3c;
ad2+ad2+da2≥3d,
bd2+bd2+db2≥3d,
cd2+cd2+dc2≥3d.
将以上十二个式子相加得
b+c+da2+c+d+ab2+d+a+bc2+a+b+cd2≥3(1a+1b+1c+1d)=3.
评注 本题还可以推广到n元(证明方法同上,具体证明留给读者).
推广2 已知a1,a2,…,an(n∈N*)是满足a1a2…an-1+a1…an-2an+…+a2…an-1an=a1a2…an的正数,求证:a2+…+ana21+a3+…+a1a22+…+a1+…+an-1a2n≥n-1.
将这道越南竞赛题中的约束条件ab+bc+ca=abc去掉,可得2005年罗马尼亚数学奥林匹克试题:
推广3 已知a,b,c是正实数,求证:b+ca2+c+ab2+a+bc2≥2(1a+1b+1c).
文[2]把此题加强为:
推广4 b+ca2+c+ab2+a+bc2
≥22c21a+1b+2a21b+1c+2b21c+1a
≥21a+1b+1c+22a-1b-1c21a+1b+1c.
同理去掉四元推广式中的约束条件abc+abd+acd+bcd=abcd有相应题目如下:
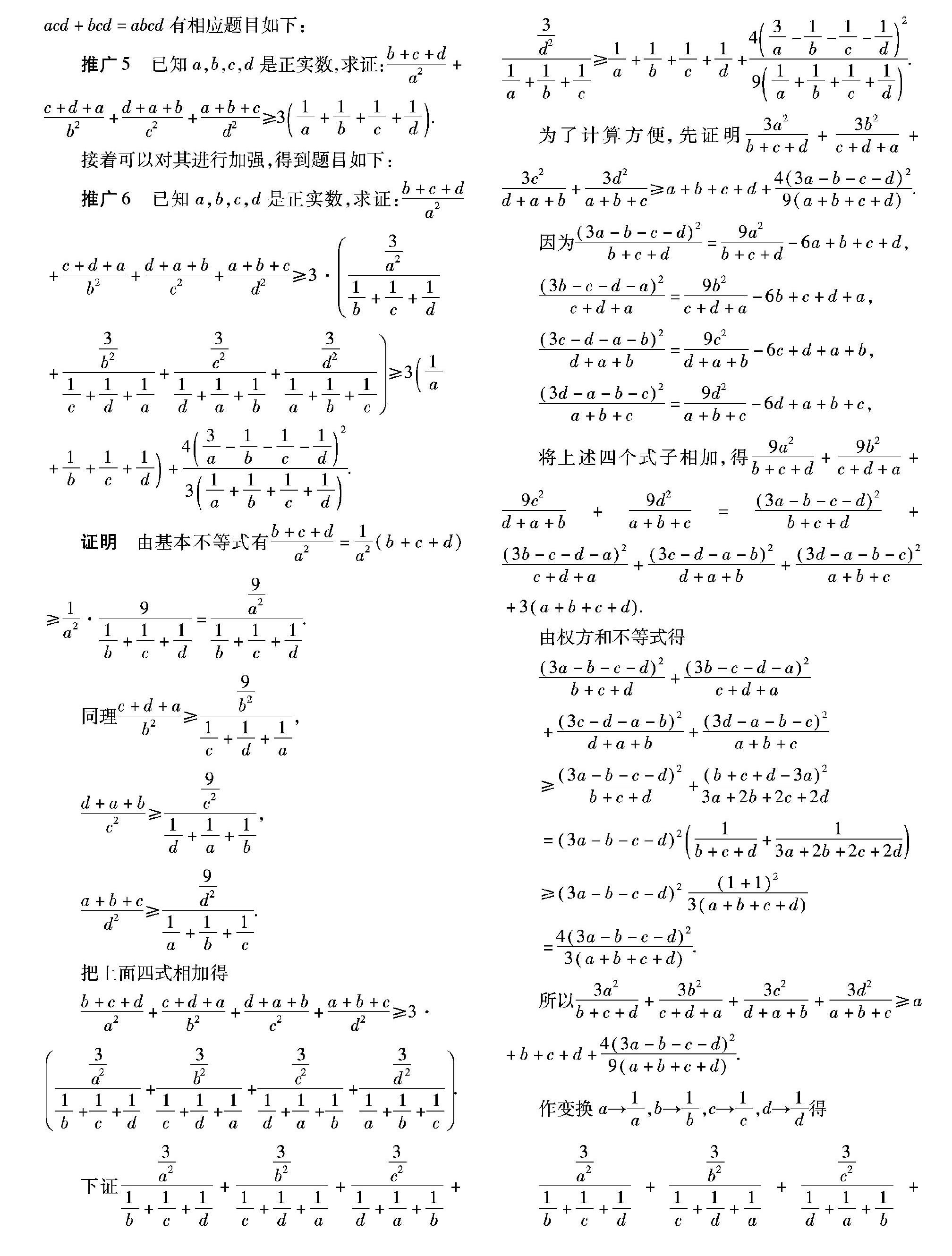
推广5 已知a,b,c,d是正实数,求证:b+c+da2+c+d+ab2+d+a+bc2+a+b+cd2≥31a+1b+1c+1d.
接着可以对其进行加强,得到题目如下:
推广6 已知a,b,c,d是正实数,求证:
b+c+da2+c+d+ab2+d+a+bc2+a+b+cd2≥3·3a21b+1c+1d
+3b21c+1d+1a+3c21d+1a+1b+3d21a+1b+1c≥31a+1b+1c+1d+
43a-1b-1c-1d231a+1b+1c+1d.
证明 由基本不等式有
b+c+da2=1a2(b+c+d)≥1a2·91b+1c+1d=9a21b+1c+1d.
同理c+d+ab2≥9b21c+1d+1a,
d+a+bc2≥9c21d+1a+1b,
a+b+cd2≥9d21a+1b+1c.
把上面四式相加得
b+c+da2+c+d+ab2+d+a+bc2+a+b+cd2≥3·3a21b+1c+1d+3b21c+1d+1a+3c21d+1a+1b+3d21a+1b+1c.
下证
3a21b+1c+1d+3b21c+1d+1a+3c21d+1a+1b+
3d21a+1b+1c≥1a+1b+1c+1d+
43a-1b-1c-1d291a+1b+1c+1d.
为了计算方便,先证明
3a2b+c+d+3b2c+d+a+3c2d+a+b+3d2a+b+c≥a+b+c+d+4(3a-b-c-d)29(a+b+c+d).
因为
3a-b-c-d2b+c+d=9a2b+c+d-6a+b+c+d,
3b-c-d-a2c+d+a=9b2c+d+a-6b+c+d+a,
3c-d-a-b2d+a+b=9c2d+a+b-6c+d+a+b,
3d-a-b-c2a+b+c=9d2a+b+c-6d+a+b+c,
将上述四个式子相加,得
9a2b+c+d+9b2c+d+a+9c2d+a+b+9d2a+b+c=
3a-b-c-d2b+c+d+3b-c-d-a2c+d+a+
3c-d-a-b2d+a+b+3d-a-b-c2a+b+c+3a+b+c+d.
由權方和不等式得
3a-b-c-d2b+c+d+3b-c-d-a2c+d+a
+3c-d-a-b2d+a+b+3d-a-b-c2a+b+c
≥3a-b-c-d2b+c+d+b+c+d-3a23a+2b+2c+2d
=3a-b-c-d21b+c+d+13a+2b+2c+2d
≥3a-b-c-d21+123a+b+c+d
=43a-b-c-d23a+b+c+d.
所以
3a2b+c+d+3b2c+d+a+3c2d+a+b+3d2a+b+c≥a+b+c+d+43a-b-c-d29a+b+c+d.
作变换a→1a,b→1b,c→1c,d→1d得
3a21b+1c+1d+3b21c+1d+1a+3c21d+1a+1b+3d21a+1b+1c≥
1a+1b+1c+1d+43a-1b-1c-1d291a+1b+1c+1d.
故
b+c+da2+c+d+ab2+d+a+bc2+a+b+cd 2≥3· 3a21b+1c+1d+3b21c+1d+1a+3c21d+1a+1b
+3d21a+1b+1c≥31a+1b+1c+1d+
43a-1b-1c-1d231a+1b+1c+1d.
注 本题还可以对n元推广式进行加强(证明方法同上,具体证明留给读者).
推广7 已知a1,a2,…,an(n∈N*)是正实数,求证:
a2+…+ana21+a3+…+a1a22+…+a1+…+an-1a2n≥n-1n-1a211a2+1a3+…+1an+n-1a221a3+1a4+…+1a1+…+n-1a2n1a1+1a2+…+1an-1≥
n-11a1+1a2+…+1an+nn-1a1-1a2-1a3-…-1an2n-11a1+1a2+…+1an.
参考文献:
[1]周瑜芽.巧用均值不等式证明2018年数学奥林匹克不等式题[J].中学数学研究,2019(03):49-50.
[2]叶大文,邹守文.若干国际国内数学奥林匹克不等式问题的加强[J].保山师专学报,2009,28(02):61-64.
(收稿日期:2019-11-13)

