一种开环输出反馈预测控制

胡建晨,王 勇,丁宝苍

(西安交通大学电子信息与工程学院,陕西西安 710049)

1 引言

模型预测控制(model predictive control,MPC)是在工业过程中得到高度认可并广泛应用的控制方法[1-2],其具有在满足操作变量(manipulated variable,MV)和状态约束的情况下在线优化的能力.通常,工业过程中应用的MPC具有递阶结构,上层实时优化(real time optimization,RTO)决定目标理想值(xt,ut)并将其传递给中间层,中间层稳态目标计算(steady state target calculation,SSTC)以跟踪上层RTO给定的目标理想值为性能指标,通过多目标协调优化得到稳态目标值,下层MPC跟踪稳态目标值得到控制作用[3-6].上层RTO通常采用稳态非线性模型(工作在小时/天级别),中间层SSTC通常采用稳态线性模型(工作在分钟级别),下层MPC 采用动态线性模型(工作在秒级别).通常,综合考虑了SSTC的MPC算法被称为双层结构MPC,简称双层MPC.双层MPC采用的线性模型可通过将非线性模型在平衡点附近线性化得到,或在工程中直接通过辨识方法得到.当系统具有模型不确定性时,传统工业预测控制方法上层优化层和下层控制层采用的模型不一致性会导致它们的稳态增益不同,而带来静差[7-8].

一般的非线性模型可被描述成线性参数时变(linear parameter varying,LPV)模型,即非线性系统动态特性可以被一组局部线性模型包含,在不同的操作条件下系统可在不同的局部线性模型之间切换[9-10].对于具有模型不确定性的系统,通常假设其具有多胞不确定性,这即是说LPV模型参数属于由局部线性模型描述的多胞内.多胞描述模型已经过学者们多年研究,基于线性矩阵不等式(linear matrix inequality,LMI)框架下给出了具有代表性的理论成果[11-16].而对于具有递阶结构的双层MPC,关于多胞描述模型的研究甚少.

考虑具有模型不确定性的系统,采用多胞描述模型代替在平衡点附近工作的线性模型.本文同时考虑状态不可测情形,需要通过可测系统输出来估计状态的实时值,利用状态的估计值对系统未来状态做预报.由于采用了多胞描述模型,每时刻状态预测方程中的参数由多胞顶点值构成,对未来状态的估计是关于未来多胞顶点状态预测值的凸组合.文献[17]通过构造参数依赖的顶点控制作用及状态预测方程,给出了开环状态反馈单层MPC控制方案.本文通过构造类似的参数依赖顶点控制作用及状态预测方程,给出了启发式开环输出反馈双层MPC方案,其中包含了SSTC层及动态控制层的设计.由于模型系数实时值未知,在SSTC层稳态目标值通常无法满足稳态LPV方程,因而在SSTC层稳态目标值应满足某个非线性方程.本文方案利用由SSTC层稳态目标值及多胞顶点值构成的稳态预测方程计算得到顶点稳态目标值,下层动态控制通过跟踪顶点稳态目标值优化得到控制作用并实施当前时刻第一步控制作用.上下层模型具有较好的一致性可以实现无静差.

现有的SSTC层虽有一些采用非线性模型,然而多数仍采用线性模型(SSTC优化问题求解得到的稳态目标变化速度不能过慢).因方案采用多胞描述模型,多个局部稳态线性模型并不能保证稳态目标值有解,文献[18]在SSTC层通过在稳态LPV模型中引入人工干扰从而保证了稳态目标值有解,同时在SSTC优化问题中惩罚人工干扰的幅值来保证解的唯一性,最终可得到最优稳态目标值与对应的人工干扰.本文利用文献[18]的稳态目标计算思路对SSTC层采用的稳态多胞描述模型引入人工干扰,同时对动态模型也引入人工干扰用来达到稳态预测方程和动态预测方程的统一,基于此改进控制方案.该方案上下层均采用具有人工干扰的多胞描述模型,同样可保证无静差.不同于文献[17-18]中求解min-max优化问题得到控制作用,本文方案采用二次性能指标,优化问题均可转化为二次规划(quadratic programming,QP)问题求解.

本文规划如下:第2章介绍多胞描述模型并引入参数依赖的顶点控制作用;第3章通过引入动态及稳态预测方程从而提出启发式开环输出反馈双层MPC整体方案;第4章基于引入人工干扰的多胞描述模型介绍改进的控制方案;第5章进行仿真验证;第6章小结全文.本文主要符号见表1.

表1 本文符号Table 1 The notations in this paper

2 问题描述

考虑如下的离散时间多胞描述模型:

其中:u∈Rm为控制输入,x∈Rn为系统状态,y∈Rr为系统输出.通常考虑如下的输入和状态约束:

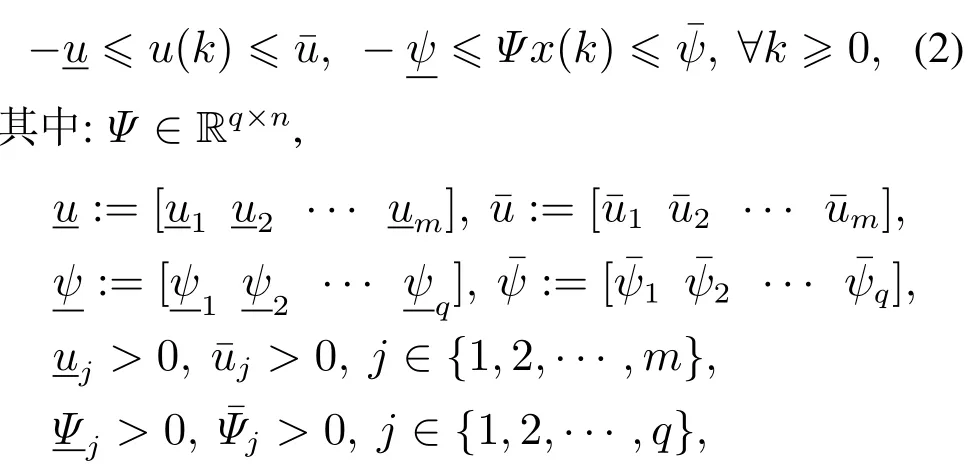
其中存在系数ωl(k)使得

令凸包

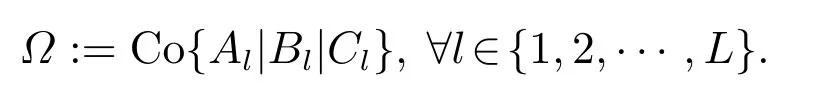
凸包的顶点值[Al|Bl|Cl]通常已知/给定,一般假设ωl(k)的实时值未知/不可测,这即是说LPV模型参数[A(k)|B(k)|C(k)]的实时值未知/不可测.假设状态x(k)不可测(或并非所有x(k)可测),输出y(k)的实时值可测,可采用如下观测器估计状态实时值:

注意到采用式(3)-(4)进行状态估计时,当前观测器系数已确定、输出y(k)可测、估计状态(k)已知,下一时刻的估计状态(k+1)可通过状态观测器得到,但未来时刻的状态(k+1+i),∀i ≥1是不可知的,需要通过动态方程进行状态预测得到.

令控制时域与预测时域为N,采用文献[17]中的方法定义依赖于多胞顶点值的未来时刻顶点控制作用u(k|k),ul0(k+1|k),···,ulN−2···l0(k+N−1|k),∀lj∈{1,···,L},j∈{0,···,N−2},使其满足状态方程

其中:i∈{1,···,N−1},lj∈{1,···,L},j∈{0,···,N−1}.式中li−1···l0(k+i|k),i∈{1,···,N}为顶点状态预测值.未来真实控制作用u(k+i|k),∀i>0依赖于多胞系数,是未知/不可测的,可表示为

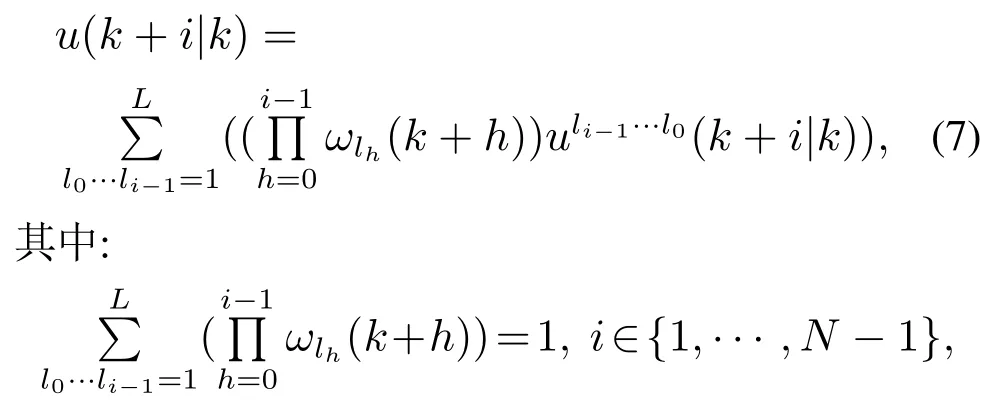
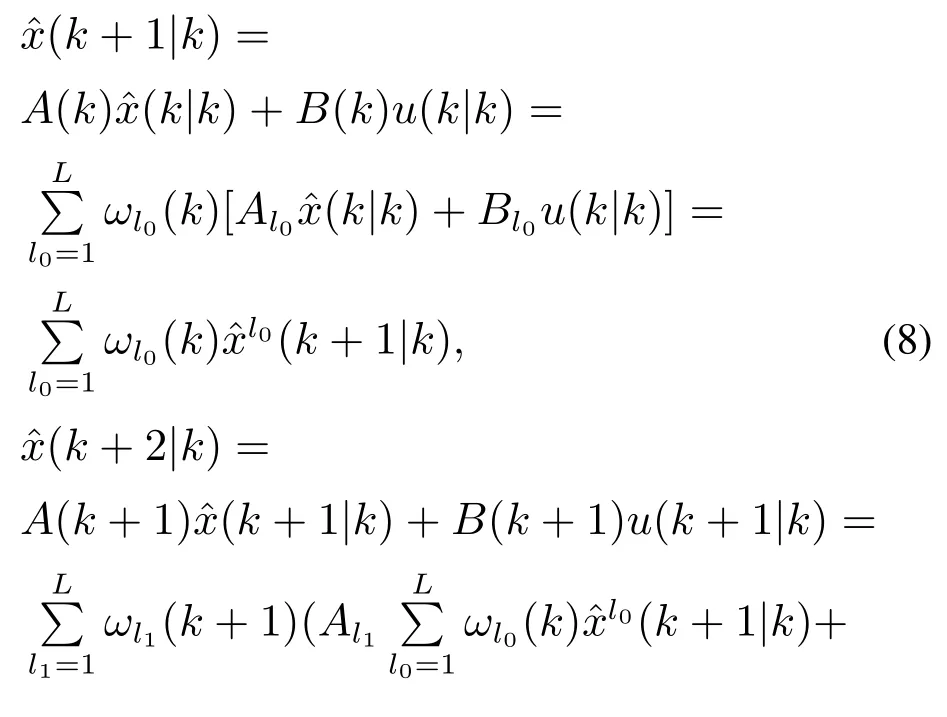
则未来时刻状态预测可写为向量形式

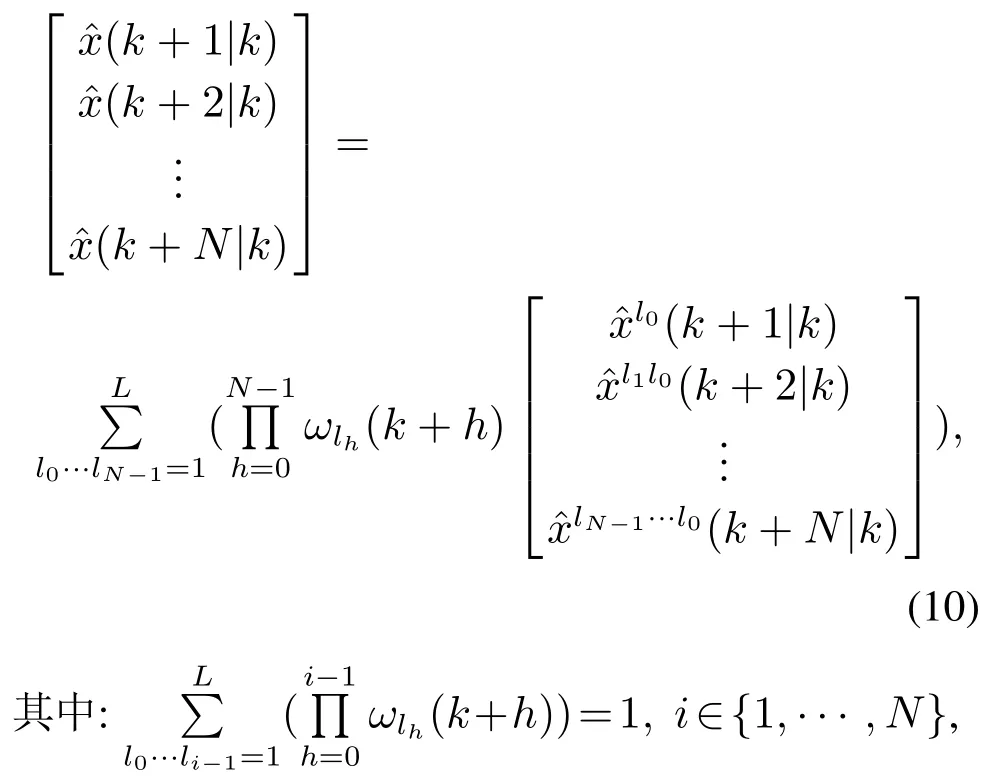
3 开环输出反馈预测控制

对于一般基于线性模型的预测控制方案中,优化问题惩罚预测状态和未来控制作用与稳态值的差值.对于本文考虑的具有模型不确定性的系统来说,多胞描述模型中的参数ω(k)未知,这意味着准确的系统状态未知.当预测时域N增加,每一个时刻的未知参数如式(10)中所示取过去时刻所有ω(k)的乘积,这便会导致随着预测时域N的增加,未来状态的不确定性指数增加.为了解决这个问题,本文引入顶点控制作用从而使得顶点预测状态跟踪其顶点稳态值,这样便可处理预测模型中不确定参数ω(k)的影响,由式(8)-(9)可推导得到基于顶点状态的稳态预测方程以及动态预测方程

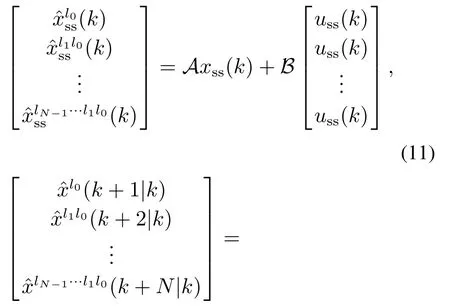
式(13)-(14)中Q1,l0,R0,Q2,l1,l0,R1,l0,···,QN,lN−1···l0,RN−1,lN−2···l0为非负加权阵.以顶点控制作用为决策变量,优化问题可构造为如下QP问题:

4 基于人工干扰的输出反馈预测控制

上一章介绍的开环输出反馈预测控制方案在SSTC层稳态目标满足某个非线性方程,而在一般的SSTC模块,考虑到计算时间通常工作在分钟级,通常采用线性模型.而针对多胞描述模型,线性稳态方程xss(k)=Alxss(k)+Bluss(k),l=1,2,···,L,通常不能被满足,文献[18]给出了一种引入人工干扰的方法使得SSTC模块可以直接采用多胞描述模型,引入人工干扰dl∈Rn使得多胞描述模型稳态方程变为

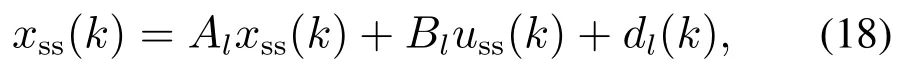
其中:AlI,∀l∈{1,2,···,L}.由于人工干扰的引入,方程(18)中变量数L+2大于方程数L,则此方程有解,且满足方程(18)的稳态目标解xss(k)和uss(k)不唯一,在SSTC优化问题中需要同时以dl(k)为决策变量.由于dl(k)为人为引入的干扰,需要在SSTC性能指标中加入使得其幅值最小化.SSTC优化问题可有多种多样的构造方法,可能包含多优先级和软约束放松,整体解决方案见文献[20]所示,本文不再赘述.

注1在一般的SSTC层中，通过优化问题得到稳态目标xss和uss.在本文构造的SSTC优化问题中,进一步得到满足式(18)的dl(k).人工干扰dl(k)为引入的决策变量.也可以看作是稳态偏置项(见文献[18]).它的主要用途是使得基于多胞描述模型的稳态方程(18)有解而引入的自由度.否则,方程(18)无法保证有解.

由于引入了人工干扰,多胞描述模型(1)变为

每个时刻求解如下二次规划问题并且取第1步u∗(k|k)送入实际系统:

5 仿真算例

考虑文献[21]中不含干扰项的非线性CSTR模型:

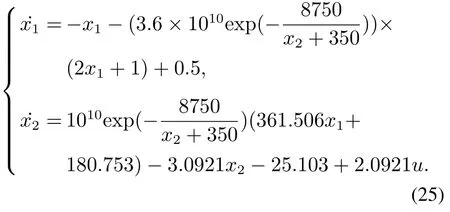
采用文献[21]中的处理办法可得到多胞描述模型,式(1)中参数为

输入与输出约束为|u|≥10 和|y|≥10,状态约束|x1|≥0.5.

取初始状态x(0)=[0.2−8]T,y(0)=3.3,目标理想值ut=2.5,xt=[−0.04 2.37]T,L0=[1 1]T,N=3,Q=10,R=1,采用本文第3章介绍的算法,在SSTC层采用稳态非线性模型,在每一时刻解优化问题(15)-(17),仿真结果如图1-3所示,可以看到控制作用和系统状态很好地跟踪了可达目标理想值,上下层的模型一致性保证了无静差.

图1 状态x1(k)响应(第3章算法)Fig.1 Response of state x1(k)(algorithm in Chapter 3)

图2 状态x2(k)响应(第3章算法)Fig.2 Response of state x2(k)(algorithm in Chapter 3)

图3 输入信号u(k)响应(第3章算法)Fig.3 Response of input signal u(k)(algorithm in Chapter 3)

采用本文第4章介绍的算法,引入了人工干扰,在SSTC层采用线性模型,仿真结果如图4-6所示,可以看到控制作用和系统状态跟踪上层稳态目标值,同样保证了无静差.

图5 状态x1(k)响应(第4章算法)Fig.5 Response of state x1(k)(algorithm in Chapter 4)

图6 状态x2(k)响应(第4章算法)Fig.6 Response of state x2(k)(algorithm in Chapter 4)

6 结论

本文给出了基于多胞描述模型的启发式开环输出反馈预测控制的两种解决方案,通过引入顶点控制作用得到顶点状态预测方程,优化问题跟踪稳态目标的顶点值得到控制作用.第3章介绍的方案适用于稳态目标值满足某个非线性方程.第4章介绍的方案适用于稳态目标值满足引入人工干扰的线性方程.两种方案均通过仿真验证了其可行性和有效性.由于采用多胞描述模型,计算量相比于一般的工业预测控制稍大.