基于模型预测的自动导引车区间轨迹跟踪控制

徐 航 ,张依恋 ,朱 瑾 ,范勤勤

(1.上海海事大学航运技术与控制工程交通行业重点实验室,上海 201306;2.上海海事大学物流研究中心,上海 201306)

1 引言

自动导引车(automatic guided vehicle,AGV),在智能交通系统的发展下,已经成为一个吸引众多学者关注的对象.对AGV跟踪控制的研究使AGV能够在不同条件下安全地进行操纵,是实现AGV智能化和实用化的一个重要部分[1-9].而如何根据当前车辆动态信息和车辆前方道路情况来设计转向和速度控制法则,是解决路径跟踪控制问题的关键[10-11].实现AGV安全稳定的路径跟踪控制具有十分重要的意义,因此,学者对AGV的路径跟踪控制展开了深入研究.

文献[12]考虑了机器人动力学模型参数的不确定性,同时,为了克服速度和力矩的跳变,加入了神经动力学模型对控制器进行优化,提出了一种自适应和神经动力学相结合的轮式移动机器人路径跟踪控制方法.文献[13]针对Mecanum轮全方位移动AGV的路径跟踪问题,提出了一种基于位姿状态和有限控制步数的路径跟踪优化控制方法,且实验表明,对于不同速度,该算法均能快速、稳定地消除位姿偏差.文献[14]利用Backstepping控制算法,针对车辆轨迹跟踪问题设计了智能小车(intelligent vehicle,IV)空间数学模型跟踪控制器.仿真结果表明,采用该方法设计的控制器可以快速跟踪预先设定的轨迹,并且在跟踪过程中保证了较高的全局稳定性.文献[15]提出了基于跟踪误差模型的无人驾驶车辆预测控制方法,保证了无人驾驶车辆快速且稳定地行驶且实时性达到给定要求.张经天等人[16]提出了一种分段预测控制模型,将预测控制器分为3段,之后解析得到最优控制变量.文献[17]对使用二维码作为定位模块的视觉自动导引车的轨迹跟踪问题进行研究,并利用一种基于最优偏差路径的模糊比例--积分--微分纠偏算法,该方法既提高了无轨导引AGV的导航精度,也较好地满足系统运行的稳定性和伺服驱动能力.以上这些方法均可以有效跟踪自动导引车的期望路径,但是都没有对车辆进行区间控制约束.

而在实际应用过程中,忽略道路宽度可能使AGV偏离期望的道路区间,忽略AGV的尺寸和形状可能使AGV发生碰撞.基于此,近年来,学者们开始对AGV运行过程中的区间控制约束进行研究.文献[18]提出了区间路径跟踪描述方法,并提出了利用模型预测控制的水平移动控制方法来讨论区间路径跟踪问题,该方法能够有效地避免在追踪更复杂道路时出现碰撞道路边界的现象.文献[19]提出了隐式线性模型预测控制方法来设计移动水平路径跟踪控制器.该控制器采用了不同的采样时间和预测范围,有效地处理了建模误差,提高了路径跟踪精度.但是文献[18-19]只对前轮转向角进行了约束,速度却是固定的,然而,在实际情况中,AGV的速度往往是可控的.因此,本文在对AGV进行区间轨迹跟踪控制时,将该方法进行改进,使被控AGV速度可变,且稳定在一定的范围内.同时,对目标函数也进行了一定的改进,使其能够快速稳定地沿着期望路径行驶.

本文基于模型预测方法对AGV区间轨迹跟踪问题进行了研究,主要工作为:1)在AGV沿着期望速度在可行区域内行驶过程中,结合实际情况,给AGV的实际行驶速度增加一个可控范围,将其设置为控制变量;2)对目标函数进行了一定的改进,在AGV行驶过程中,增加了对偏航角的限制,可使AGV更加迅速稳定地行驶在可行区域内.

2 问题描述

传统轨迹跟踪问题都是将AGV看作一个刚性点,不考虑AGV的尺寸和形状,本文采用文献[18]提出的区间路径跟踪描述方法对AGV进行区间轨迹跟踪研究,AGV道路模型如图1所示.AGV检测到的可行区间为f1(x)和f2(x)之间的区间,所围可行区间的中心线即为期望路径.为了避免碰撞,假设AGV的宽度为w,简化车辆行驶道路模型,则AGV 可行区间将变为f3(x)=f1(x)−w/2 和f4(x)=f2(x)+w/2 之间的区间.假设f(x)是XOY 横向位置,ψ是AGV偏航角,s 为AGV 侧滑角,AGV 重心到前端的距离为l1,AGV重心到后端的距离为l2.简化后的AGV的前端横向位置为fl(x)=f(x)+l1sin(ψ+s),后端横向位置为fr(x)=f(x)−l2sin(ψ+s).同时,考虑到大多数道路为小曲率,因此,偏航角和车辆侧滑角的正弦可以简化为sin(ψ+s)≈(ψ+s),则AGV的可行区间为

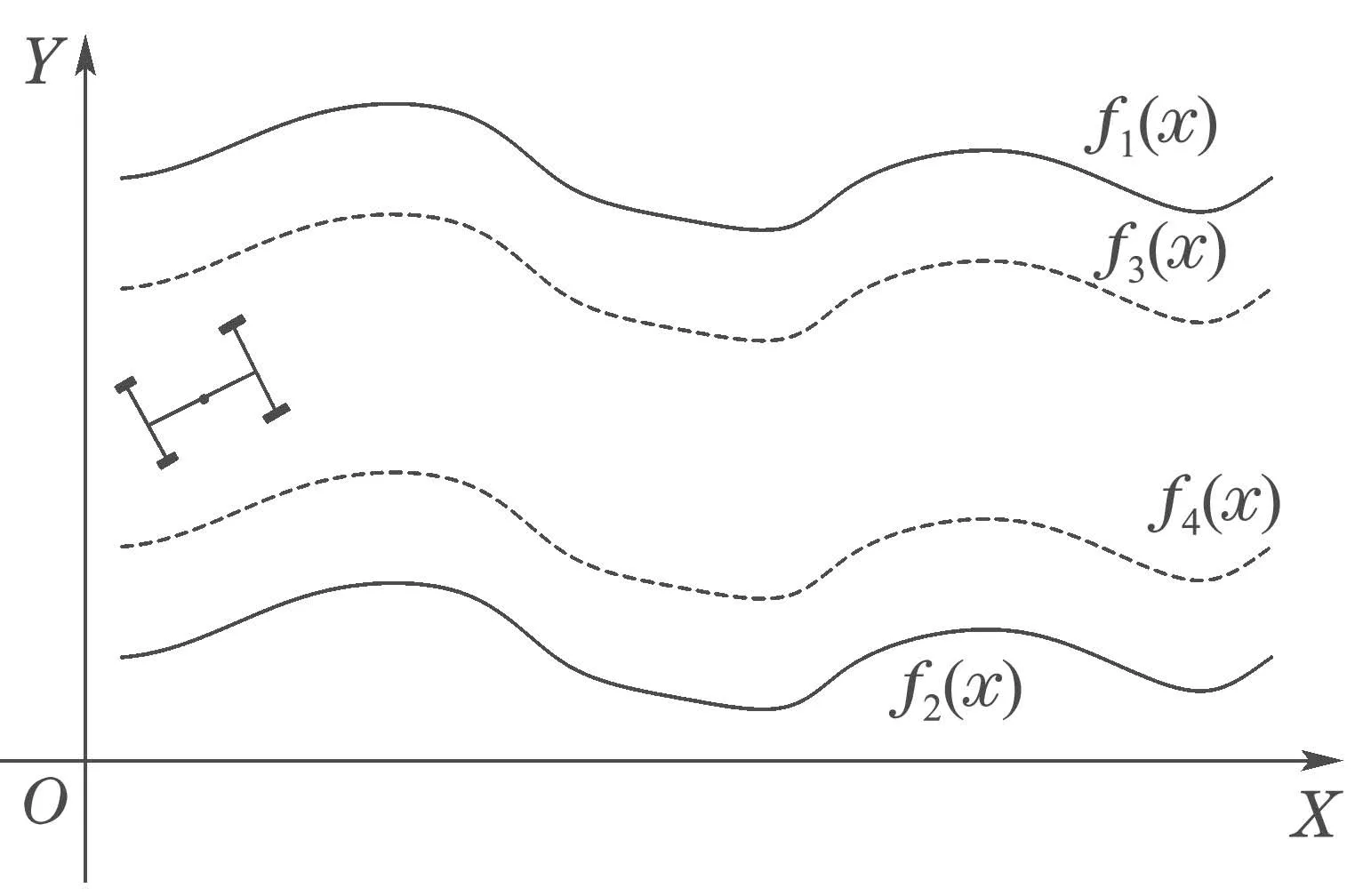
图1 车辆道路模型Fig.1 Vehicle road model

3 车辆模型

由于大多数道路均为小曲率,因此AGV的侧滑角和偏滑角在采样时间内的变化很小[18],故图2所示的运动学模型可以被描述为

图2 运动学模型Fig.2 Kinematics model

忽略车辆的纵向动力学,车辆的横向动力学如图3所示,轨迹跟踪控制器的设计模型为

其中:m为AGV的质量;前后轮胎的轮胎力分别为Fyf=Cfαf,Fyr=Crαr,Cf和Cr分别为前后轮胎侧偏刚度;v是AGV的速度;Iz为AGV的惯性矩;前后轮的侧滑角近似为

图3 运动学模型Fig.3 Kinematics model

离散化连续时间模型,得到离散时间模型

注意到文献[18]中,AGV的速度是给定的,控制变量为δ,而本文考虑到实际情况中AGV运行速度受到外界环境等因素影响,单一的定值往往不能满足AGV对外界环境的适应,因此,设定控制变量为[v δ],使得AGV能够在一定的速度和前轮转向角范围内寻找到最佳速度和最佳前轮转向角,进而行驶在可行区域内.

4 控制器设计

应用模型预测控制方法来讨论轨迹跟踪控制器的设计,控制方案的结构如图4所示.

图4 轨迹跟踪控制器的设计Fig.4 Design of the trajectory tracking controller

如果系统的控制时域为Nc,预测时域为Np,那么,预测时域内的状态量和系统输出量可由下式计算得出:

为了使整个关系看起来更加清楚明确,将系统未来时刻的输出以矩阵的形式表达,如下式所示:

由式(7)可知,预测时域内的状态量和输出量都可以通过系统初始状态量x(k|k)和控制量U(k)来计算.然而实际上,系统的控制量是未知的,只有设置合适的优化目标并对其求解,才能得到控制序列.

考虑到系统对期望路径的跟随能力,最小化成本函数

其中R(k)为期望路径.

考虑到对控制增量的约束,使控制增量平稳变化:

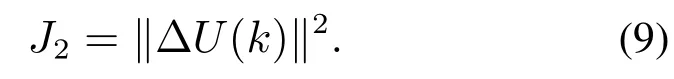
考虑到行驶路线的最短,确保低能耗:

考虑到对偏航角的约束,使其更快更稳定地沿着期望路径行驶:

引入权重因子,因此,多目标函数如下所示:

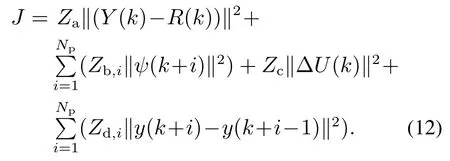
其中:Za=diag{Za,1,Za,2,...,Za,Np}>0,Zb,i>0, Zc=diag{Zc,1,Zc,2,...,Zc,Np} > 0, Zd,i> 0.Za,i,Zb,i,Zc,i,Zd,i的选取将根据实际工程情况进行确定.

区别于文献[18]中目标函数的选取,本文在目标函数中加入了对偏航角的约束,使得偏航角趋向于0,从而让AGV能够最大限度地沿着期望路径行驶,稳定地维持在可行区域内.

同时,在实际控制系统里,需要满足如下约束条件:

控制量约束:

控制增量约束:

输出约束:

综上,区间轨迹控制问题可以转化为以下优化问题中提出的模型控制预测问题:

通过求解式(16),即可实时得到未来一段时间的控制序列.

5 仿真

本文选择用MATLAB进行仿真实验,考虑AGV进行直线运动以及小曲率正弦曲线运动两种情况.参考轨迹点数量N设定为300,采样周期Ts为0.05 s,采样时间T为15 s,y为输出变量,u=[v δ]为控制变量,=[x y ψ s γ]为状态变量,AGV期望速度设定为1 m/s,速度可控范围设定为在期望速度上下0.2 m/s浮动,即[0.8,1.2]m/s,AGV期望前轮转向角设定为0,前轮转向角可控范围设定为在期望前轮转向角上下0.64 rad浮动,即[−0.64,0.64]rad.为了证明方法的可行性,采用了文献[18]里根据实际小车红旗HQ430给出的参数,如表1所示.

表1 控制器和车辆参数的一部分Table 1 Part of the controller and vehicle parameters

为了验证本文提出的区间轨迹跟踪控制方法的可行性与有效性,采用本文提出的方法以及文献[18]中提出的方法分别进行了MATLAB实验.考虑AGV做直线运动以及小区率正弦曲线运动两种情况,实验结果如下:

1)AGV做直线运动.

当AGV行驶的期望轨迹设定为直线时,其仿真结果如图5-9所示.

图5 采用本文提出的方法得到的轨迹跟踪仿真结果Fig.5 Trajectory tracking simulation results obtained by the method proposed in this paper

图6 采用文献[18]方法得到的轨迹跟踪仿真结果Fig.6 Trajectory tracking simulation results obtained by the reference [18]

图7 状态变量随时间变化结果Fig.7 State variables change over time

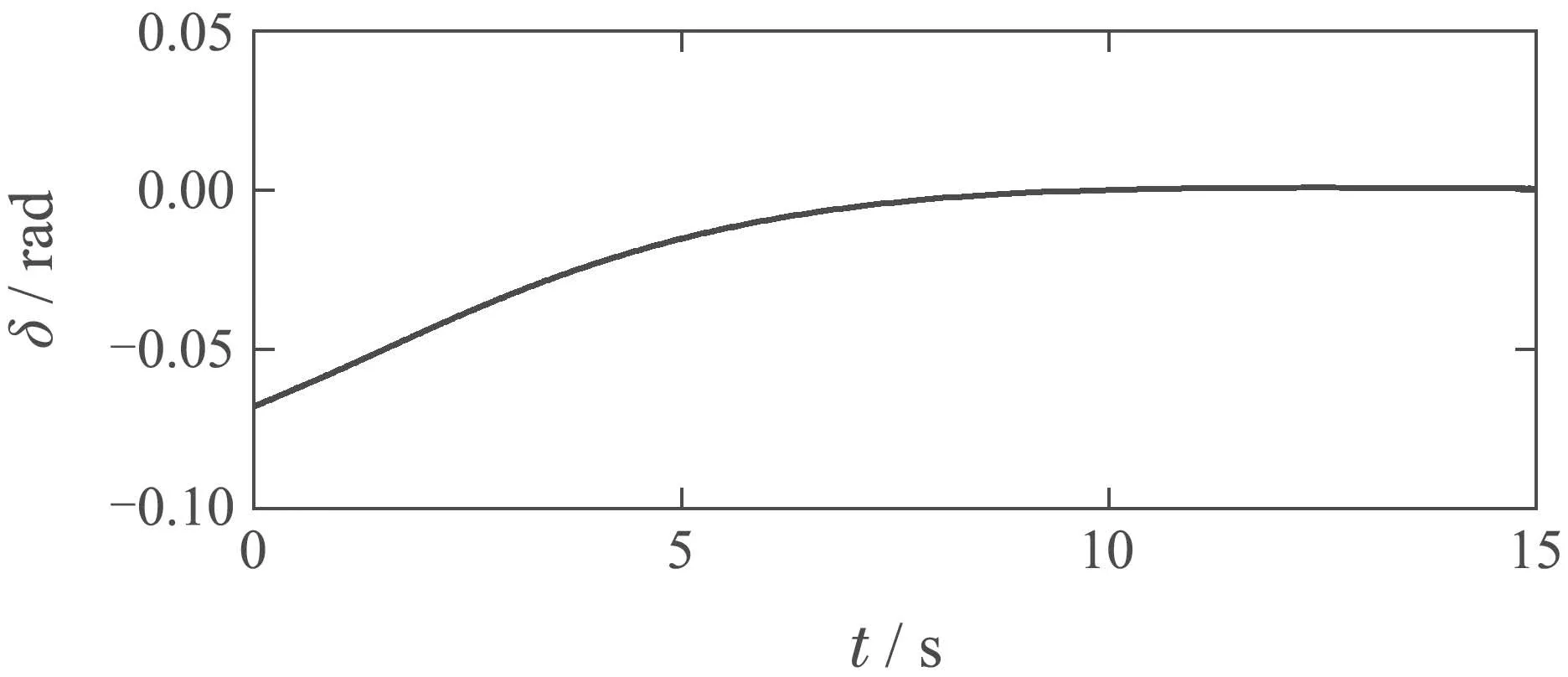
图8 控制变量随时间变化结果Fig.8 Control variables change over time

图9 误差分析Fig.9 Error analysis

其中,图5和图6分别用本文提出的方法以及采用文献[10]的方法得到的轨迹跟踪仿真结果.图中:点线表示AGV实际行驶轨迹,直线表示AGV期望行驶轨迹,两条点划线之间的区域表示给定的AGV可行区间范围.从图5和图6中可以看到AGV均稳定地行驶在可行区间内,且经过一段时间后,与期望轨迹基本重合.但同时,通过图5和图6,也可以清楚的看到,采用本文提出的方法偏离期望轨迹的幅度较小,也更快更稳定地沿着期望轨迹行驶.

图7表示采用本文提出的方法得到的状态变量随时间变化的结果,图7从上到下依次为AGV的横向位置、纵向位置、偏航角、侧滑角和偏航率随时间变化的结果.图中:直线表示AGV的横向位置、纵向位置、偏航角、侧滑角和偏航率的期望值,虚线表示实际值.由图可知,采用本文提出的方法能够使得AGV实际行驶的横向位置与AGV期望行驶的横向位置基本重合,并且,经过一段时间后,AGV实际行驶的纵向位置稳定在期望轨迹上,AGV的偏航角、侧滑角和偏航率也无限趋近于0.

图8表示采用本文提出的方法得到的控制变量随时间变化的结果,由图可知,AGV速度经过一段时间内的变化迅速稳定在一个最优值,AGV的前轮转向角经过一段时间逐渐趋向于0,且AGV的速度和前轮转向角均稳定在给定范围内.

图9从上到下依次为采用本文提出的方法得到的AGV实际行驶轨迹与期望轨迹的误差距离,实际偏航角与期望偏航角之间的误差角度以及实际侧滑角与期望侧滑角之间的误差角度.由图9可以看出,经过一段时间后,上述误差均趋近于0.

2)AGV做小曲率正弦曲线运动.

当AGV行驶的期望轨迹设定为小曲率正弦曲线y=sin(k×T/3)/3 时(k=1,2,···,N),其仿真结果如图10-14所示.

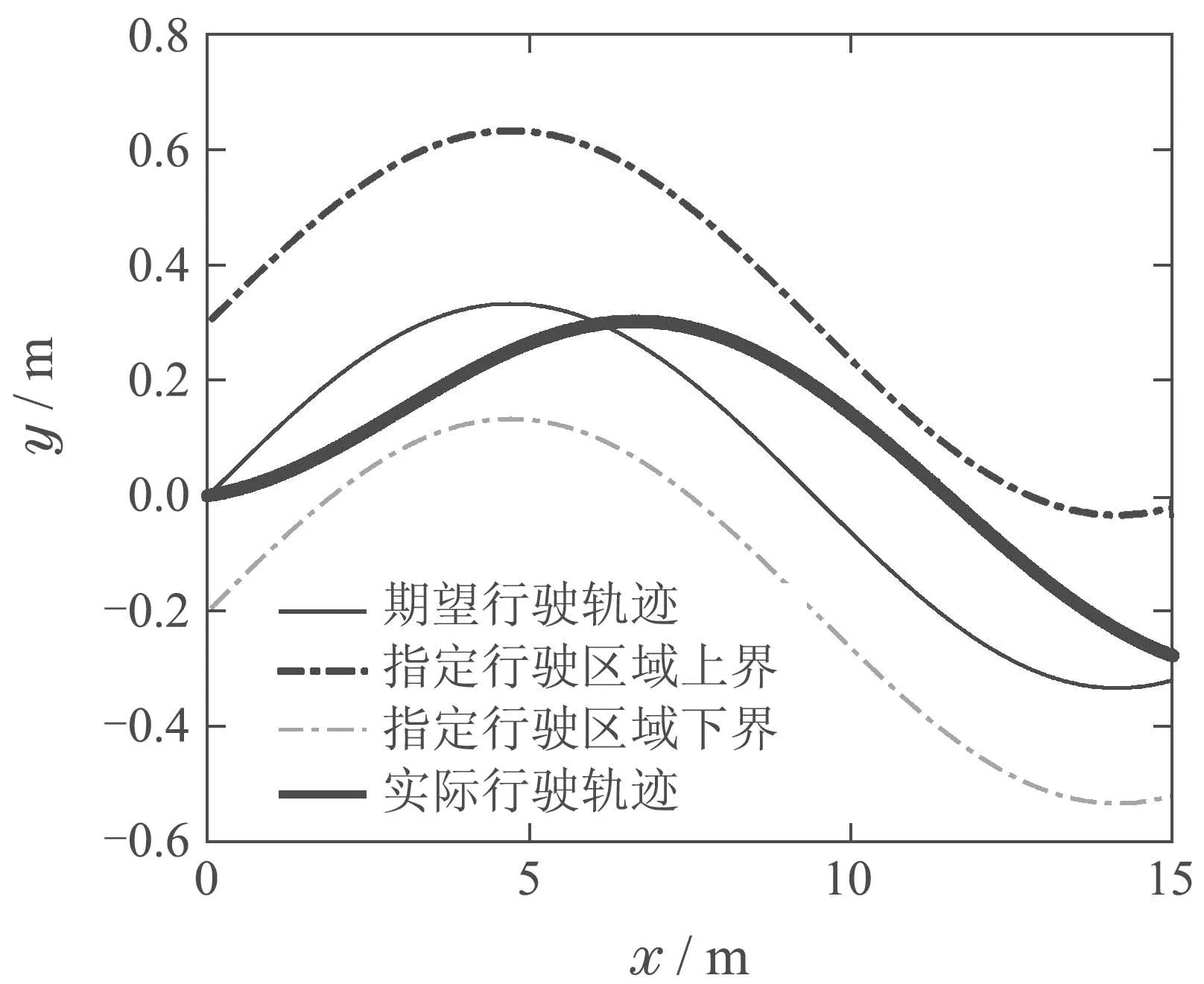
图10 采用本文提出的方法得到的轨迹跟踪仿真结果Fig.10 Trajectory tracking simulation results obtained by the method proposed in this paper

图11 采用文献[18]方法得到的轨迹跟踪仿真结果Fig.11 Trajectory tracking simulation results obtained by the reference [18]

图12 状态变量随时间变化结果Fig.12 State variables change over time

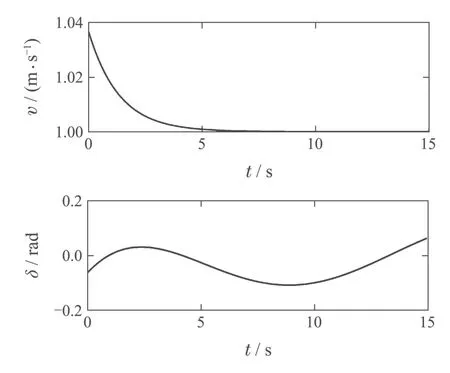
图13 控制变量随时间变化结果Fig.13 Control variables change over time

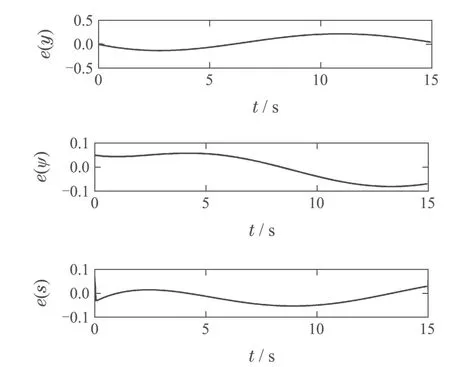
图14 误差分析Fig.14 Error analysis

其中,图10和图11分别为用本文提出的方法以及采用文献[18]的方法得到的轨迹跟踪仿真结果.从图10和图11中可以看到AGV均稳定地行驶在可行区间内.但同时,通过图10和图11,也可以清楚的看到,相对于文献[18]的方法在转弯时可能会无限趋近于可行域边界,采用本文提出的方法能够更加平稳的行驶在可行区间内.

图12表示采用本文提出的方法得到的状态变量随时间变化的结果,图12从上到下依次为AGV的横向位置、纵向位置、偏航角、侧滑角和偏航率随时间变化的结果.由图可知,AGV实际行驶的横向位置与AGV期望行驶的横向位置基本重合,AGV实际行驶的纵向位置稳定在AGV的期望区间范围内.并且,由于AGV的期望路径设定为小曲率曲线,因此,AGV的偏航角,侧滑角和偏航率也一直在0上下小范围浮动.

图13表示采用本文提出的方法得到的控制变量随时间变化的结果.由图可知,AGV速度经过一段时间内的变化迅速稳定在一个最优值,AGV的前轮转向角由于期望路径设定为小曲率曲线,也一直在0上下小范围浮动,且AGV的速度和前轮转向角均稳定在给定范围内.

图14从上到下依次为采用本文提出的方法得到的AGV实际行驶路径与期望路径的误差距离、实际偏航角与期望偏航角之间的误差角度以及实际侧滑角与期望侧滑角之间的误差角度.由图14可以看出,由于期望路径设定为小曲率曲线,上述误差均一直在0上下小范围浮动.

通过实验1)和实验2)可知,不论期望路径是直线还是小曲率正弦曲线,采用本文提出的方法,AGV经过一段时间后,迅速驶向期望路径,且始终稳定地保持在可行域内行驶.且相对于文献[18],均有一定的优化,验证了该方法的可行性与有效性.

6 总结

本文针对AGV的跟踪控制问题,设计了一种基于模型预测的AGV区间轨迹跟踪控制器,该方案选取了前轮转向角和速度作为控制变量,且对其设定了一定区间的可控范围,又利用了预测路径与期望路径之间的误差,并加入了对AGV偏航角的约束条件,最后运用模型预测控制方法通过优化得到使性能指标最优的控制序列,使AGV的轨迹跟踪快速趋于稳定.最后,在MATLAB上仿真验证了该方法的可行性与有效性.然而,笔者也注意到,在AGV做小曲率运动时,虽能够稳定行驶在可行区间内,误差却一直存在,因此,在今后的工作中,笔者将重点考虑如何减小AGV做曲线运动时的误差以及对目标函数进行进一步优化.