机械臂的自适应径向基函数神经网络双二次泛函最优控制
廖列法,杨翌虢
(江西理工大学信息工程学院,江西赣州 341000)
1 引言
随着工业自动化的不断发展,动态系统的最优控制得到了迅速发展并取得了显著成效.最优控制是使被控系统的性能指标实现最优化的一种综合策略,可概括为:对一个受控的动力学系统或运动学过程,设计最佳的控制策略,使系统的运动在由某个初始状态转移到指定的目标状态的同时,其性能指标(称为泛函)值为最优.最优控制问题广泛存在实际的生产中,例如,对于行星着陆器的动力下降阶段的控制问题,期望对参考轨迹的跟踪效果优良以及燃料消耗最少;对于机械臂系统的控制问题,期望机械臂系统的跟踪误差越小越好[1]等.
针对非线性双二次型目标泛函由跟踪误差及控制动作规律共同决定的问题,其控制规律具有时变、多输入变量、强耦合及动态震荡等特性,如何在系统控制过程中使用不大的控制量来保持较小的跟踪误差成为了影响控制系统泛函关键因素之一.近年来,针对非线性系统的控制规律的设计成为了国内外学者研究热点,如精确线性化[2-3]、自适应控制[4-5]、滑模控制[6-7]、模糊控制[8-9]、反演控制[10]及神经网络控制[11-13]等.文献[14]针对单输入单输出非线性系统,提出自适应最优控制法,实现自适应动态规划及动态面技术,文献[15-16]针对非线性系统设计自适应神经网络前馈控制器,解决状态反馈最优控制问题,等等.以上文献提高了控制器的自适应最优控制.而文献[17-18],通过引入额外的神经元,并作用于动态拉格朗日乘子,实现约束二次型优化问题的最优求解;文献[19-20]使用不连续的硬限制激活函数,实现对二次规划模型的优化求解.但以上所述文献未对双二次型泛函中二次项系数权衡比重问题展开研究,即控制能量和控制误差的权值比重问题.本文针对机械臂控制系统最优问题提出一种新型的二阶段叠加优化的双二次型最优泛函求解模型,在控制精度、收敛性、计算复杂度及数值稳定性等方面进行了优化,同时实现非线性系统中用不大的控制量来保持较小的控制误差的最优控制目标.
在本文中,如图1所示为基于非线性多关节机械臂系统.

图1 多关节机械臂系统Fig.1 Multi-joint robotic arm system
首先,在控制器的设计方面,设计一种线性误差函数,作用于非线性控制方程,并采用径向基函数(RBF)神经网络自适应逼近非线性控制方程中存在的不确定项,构成闭环最优反馈系统.在自适应激励函数的设计上,本文对比分析了常见的Gaussian 函数、Sigmoid函数及Tan-Sigmoid 函数,理论分析及数值验证了激励函数为Gaussian函数的RBF网络能有效避免局部极值,提高自适应稳定性;其次,引入一种新型的类递归神经网络[21]求解带约束条件的双二次规划问题,对比现有求解模型,例如基于拉格朗日神经网络[22]、基于梯度的神经网络[23]及双神经网络[24]等.本文理论分析及数值实例仿真验证了所提模型有效提高非线性系统的控制精度、稳定性、鲁棒性及自适应性.实现在非线性系统中用不大的控制量来保持较小的控制误差的非线性双二次型泛函最优控制.
本文的主要贡献有:
1)针对实现最优控制的核心问题,主要实现以下3个目的:其一,保持系统从初始态到末端态时系统实际状态紧跟系统理想状态变化,即保持跟踪误差趋于0值附近的控制跟踪目的;其二,通过限制系统控制动作矢量的幅值及平滑性来保证系统的稳定运行,即降低系统实现代价的节能目的;其三,设计自适应逼近控制律及双二次型求解模型,实现稳定逼近及快速收敛,即系统控制律的稳定逼近及快速收敛的目的.
2)针对非线性机械臂控制系统,设计一种线性误差函数,作用于非线性控制方程,并采用一种基于神经网络自适应逼近控制器,构成全局稳定的闭环反馈系统,实现线性函数对非线性系统的控制目的.
3)对比不同的激励函数自适应算法逼近控制律,理论说明及数值仿真验证了采用基于Gaussian函数RBF神经网络,可以达到快速学习并避免局部极值的目的,有效提高系统的控制精度、稳定性、鲁棒性及自适应性.
4)设计复合双二次规划模型,将待求参数复合成一个未知矢量,同时本文设计一种新型的类递归神经网络求解法[21]求解待带约束的双二次规划模型,有效提高了有限时间收敛速度,实现本文所述模型对非线性系统的最优控制目的.
本文行文组织结构为:首先,双二次型目标泛函最优控制描述及机械臂动力学方程的建立;其次,神经网络自适应逼近控制器的设计;再次,双二次型泛函模型的构建与求解;最后,基于二关节机械臂控制系统数值仿真验证本文所提模型.
2 问题描述
2.1 双二次型最优控制描述及机械臂动力学方程的建立
1)连续时间非线性双二次型目标泛函为

式中:M1∈Rn×n,M2∈Rn×n且M1=≥0,M2=≥0为加权矩阵;(t)∈Rn×1为跟踪误差矢量;u(t)∈Rn×1为最优控制动作矢量;t0和tf分别表示初始状态时刻及末端状态时刻;T(t)M1(t)表示控制过程中状态偏差;uT(t)M2u(t)表示控制过程中所消耗的控制能量.
2)设计n关节机械臂动力学方程为
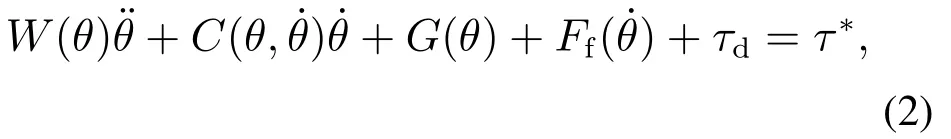
式中:θ∈Rn为广义节点位置坐标矢量;∈Rn,∈Rn分别为广义速度矢量及加速度矢量;W∈Rn×n为关节空间动力学模型的惯性矩阵;C∈Rn×n表示离心力、法向力和哥氏力之和;G∈Rn×1表示为重力项;τd∈Rn×1为其他未知外加扰动;τ∗∈Rn为动力学控制输入.
2.2 自适应神经网络逼近控制器设计
1)控制器的设计.
定义θ的跟踪函数为

式中θd(t)为理想状态下的广义节点位置坐标矢量,则
定义线性误差函数为

设计控制律为

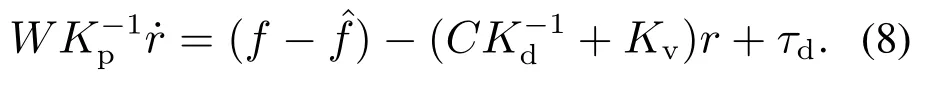
设计定义Lyapunov函数为
2)自适应RBF神经网络逼近及稳定性分析.
注1正则化径向基函数神经网络由3层组成:第1层是由输入节点组成,输入节点的个数等于输入向量x的维数;第2层为隐含层,是由直接与输入节点相连接的节点组成,一个隐含节点对应一个训练数据点,其个数与训练数据点的个数相同;第3层为输出层,包括若干个线性单元,每个线性单元与所有的隐含节点相连,即表示为网络的最终输出是由各个隐含节点输出的线性加权和.其网络如图2所示.

图2 RBF神经网络结构Fig.2 RBF neural network structure
设计激励函数为Gaussion函数的RBF神经网络对式控制系统进行RBF自适应逼近,如图3所示,基于Gaussion函数的RBF神经网络算法为

式中:x 为RBF 神经网络的输入信号,ci和σ 分别为RBF网络隐节点中心向量及标准化常数.

图3 采用RBF自适应逼近Fig.3 Using RBF adaptive approximatio n
采用基于Gaussion函数为激励函数的RBF神经网络自适应逼近训练式(6)中f(q),则输出自适应逼近值(q)为
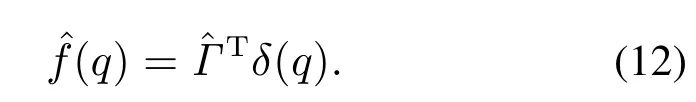
将式(12)代入式(7)得逼近控制律为
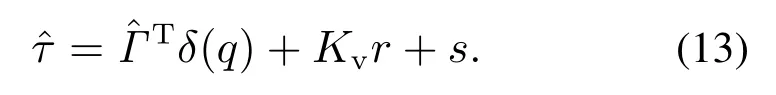

令Lyapunov函数为
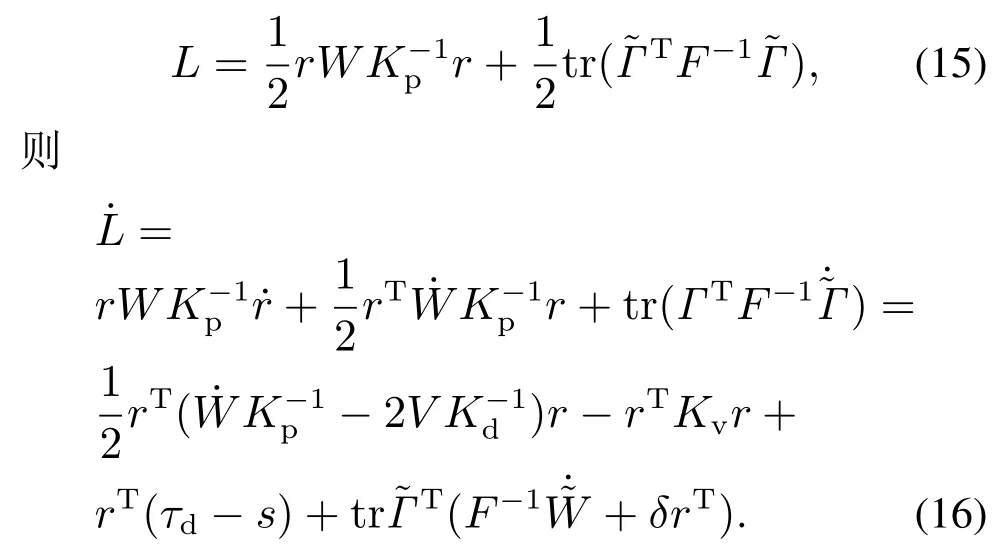
设计RBF网络自适应律为

式 中:缩放因子Z=diag{z1,z2,···,zn},z1,z2,···,zn为常量,则

设计控制误差s=(sn+sd)sgn r,则式(16)可化为
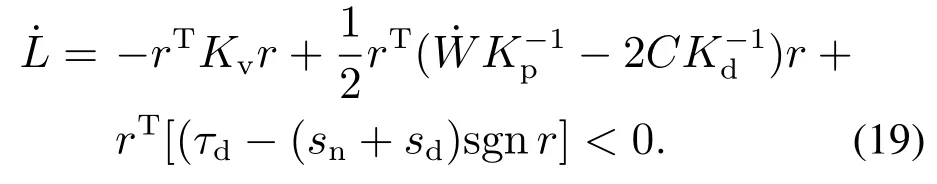
根据LaSalle不变集原理,Lyapunov函数收敛,得证系统稳定.
3)针对f(q)整体中各项分别自适应RBF逼近.
控制律如式(13)所示,其中被控对象中f(q)如式(6)所示,采用RBF网络对f(q)中各项分别进行逼近,得
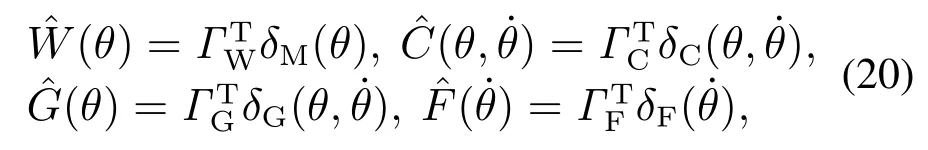
式中:ΓΘ为网络自适应律,δΘ为其激活函数,如式(11b)所示,其Θ分别代表M,C,G,F,求得自适应逼近估计值分别为此处神经网络输入信号为x=θ,x=或(θ,),求得其自适应逼近值.则式(6)中f(q)的自适应逼近值(q)为

综上所述,控制系统逼近控制律如式(13)所示,RBF网络自适应逼近律如式(17)所示,则自适应逼近状态下的机械臂动力学方程式(2)可化为

4)BP网络及RBF网络设计逼近器对比.
从理论上而言,BP网络和RBF网络类似,都可以任意精度逼近任何非线性函数,两者的主要区别为在非线性映射上采用了不同的作用函数,其逼近性能也不同.
若设计基于Sigmoid函数或Tan-Sigmoid作为激活函数的BP 网络,则式(11b)变更为
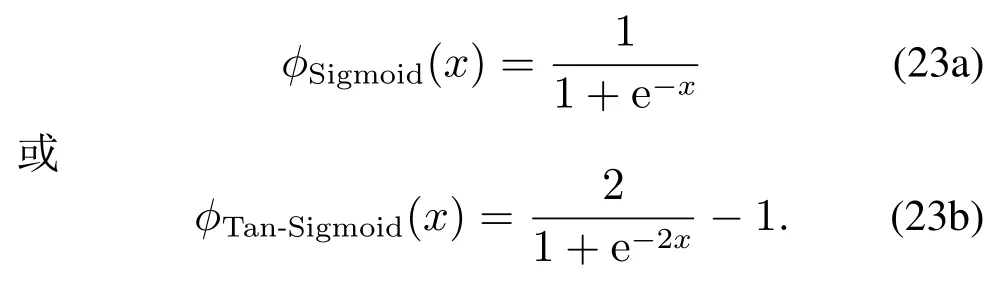
如图4所示,Sigmoid 函数的特点是将(−∞,+∞)范围内的数据映射到有限区间(0,1),Sigmoid函数将偏离原点区域的数据压缩,而靠近原点区域的数据则被放大,经Sigmoid函数处理之后,绝对值大的数据变为更加接近,而绝对值较小的数据则由于区间被放大显着更为稀疏.而Tan-Sigmoid函数将输出限定在有限区间(−1,1)之内(如图4所示).从理论上来看,BP网络中激励函数采用Sigmoid函数或Tan-Sigmoid函数,其两者函数值在输入空间中无限大范围内为非零值,即作用函数为全局的.而RBF网络采用的激励函数为Gaussion函数(如图4所示),其函数在无限大范围内趋近于零,即作用函数是局部的.综上所述,通过如图4所示对比可知,采用Gaussion函数作为隐含层激励函数的RBF网络具备收敛速度快、稳定性好、唯一逼近、无局部极小值等优点.


图4 Sigmoid函数、Tan-Sigmoid函数及Gaussian函数训练原始数据对比效果Fig.4 Contrast effect of training original data of Sigmoid function,Tan-Sigmoid function and Gauss function
2.3 双二次型性能泛函指标
1)二次型目标泛函约束方程的建立.
设计自由度为n 的多机械臂系统控制方程为τj=Pu,其中u为如式(1)所示的最优控制动作矢量(待求矢量),P∈R1×n为将控制动作矢量u映射到广义空间的线性变换.则:
机械系统参考控制动作值为
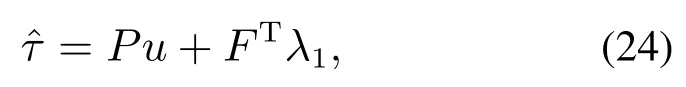
式中:F为如注2所示,由动力学机械系统约束引起的雅可比约束;λ1为比例缩放因子.联立式(22)和式(24)并代入(t)=(t)−(t)得

注2以二关节机械臂系统为例,关节末端节点位置直角坐标(x,y)与关节角位置(θ1,θ2)关系,即速度级(正向)运动学方程及逆运动学方程[25].
如图5所示为二关节为例的运动学示意图,其运动学方程为

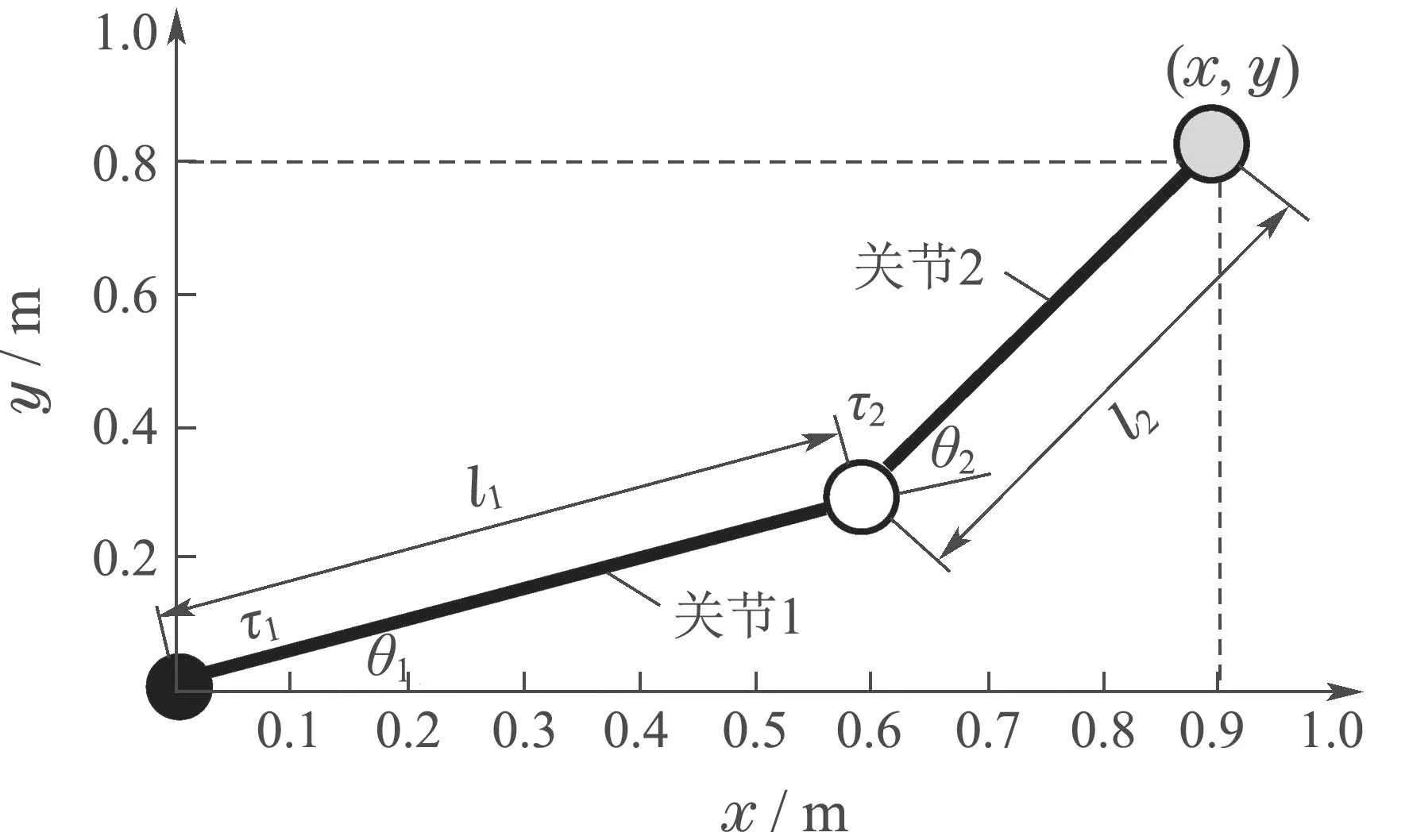
图5 二关节机械臂运行学示意图Fig.5 Operational schematic diagram of two-joint manipulator
1)加速度级运动学方程.
对式(26)两边分别对时间t求导得其操作速度和广义关节速度关系为
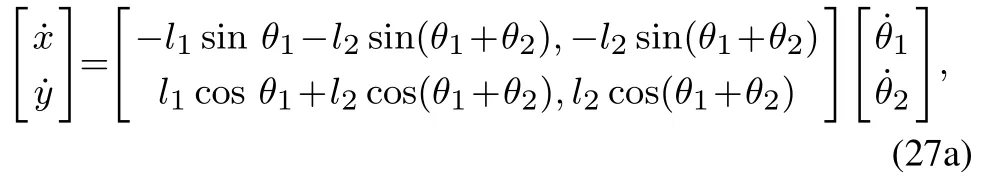

2)逆运动学方程.
对式(26)求其平方和:
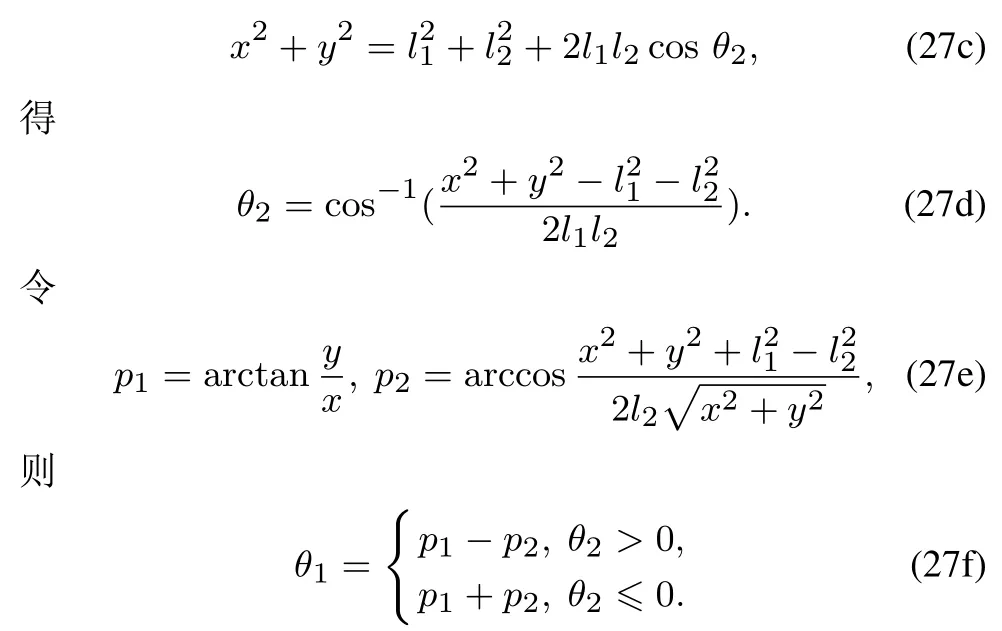
如注2所示,根据机器人学动力学相关理论[25]可得:对于n自由度,m个末端运动参数(n>m)的机械臂运动系统,其加速度级运动学方程为

在本控制系统设计中,其机械臂关节末端速度(vx,vy)保持匀速运动,令机械臂关节末端加速度=(,)=0,则设计系统正向运动学方程为


由式(1)连续时间非线性双二次型目标泛函得
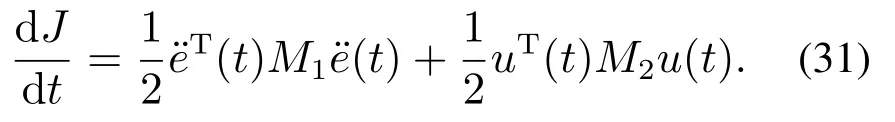
1)等式约束条件为

2)不等式约束条件为
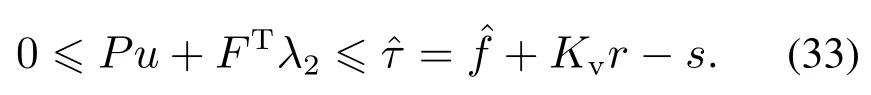
其物理意义为机械系统非零控制动作矢量与电机正常反应和摩擦力所引起的动作矢量应小于控制律,通过限制系统控制动作矢量的幅值间接体现最优控制的目的.其中为式(13)所求数值.
2)双二次型性能泛函指标模型的建立.
连续时间非线性双二次型性能目标泛函可抽象为二次规划的复合(双二次型)求解问题
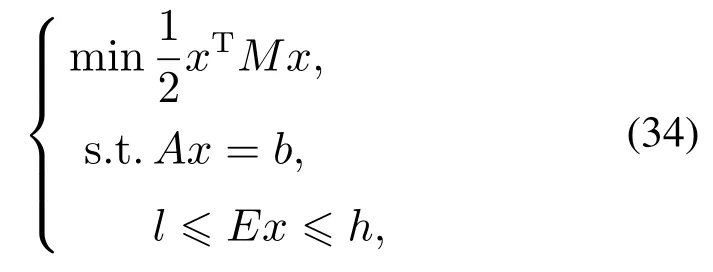
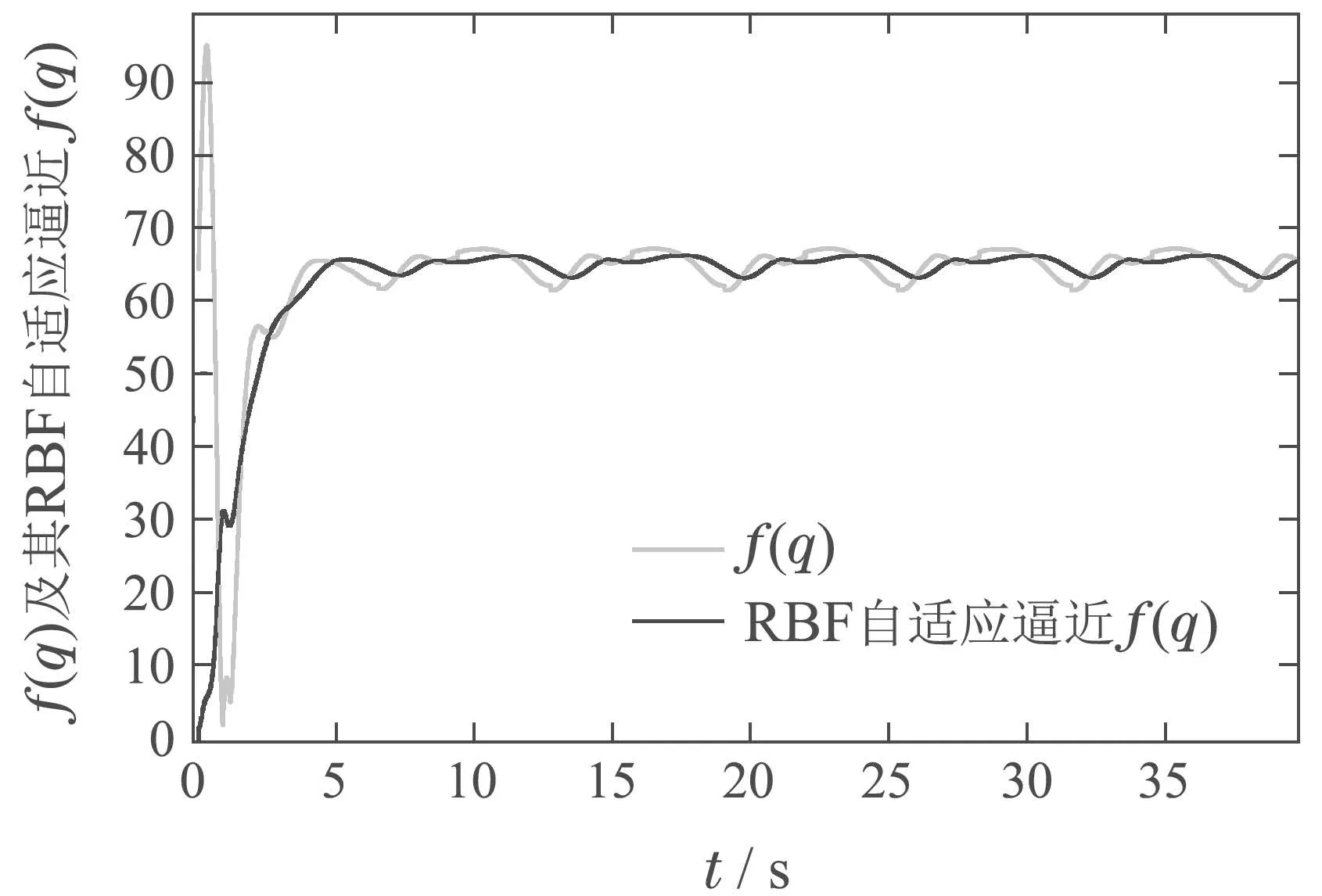
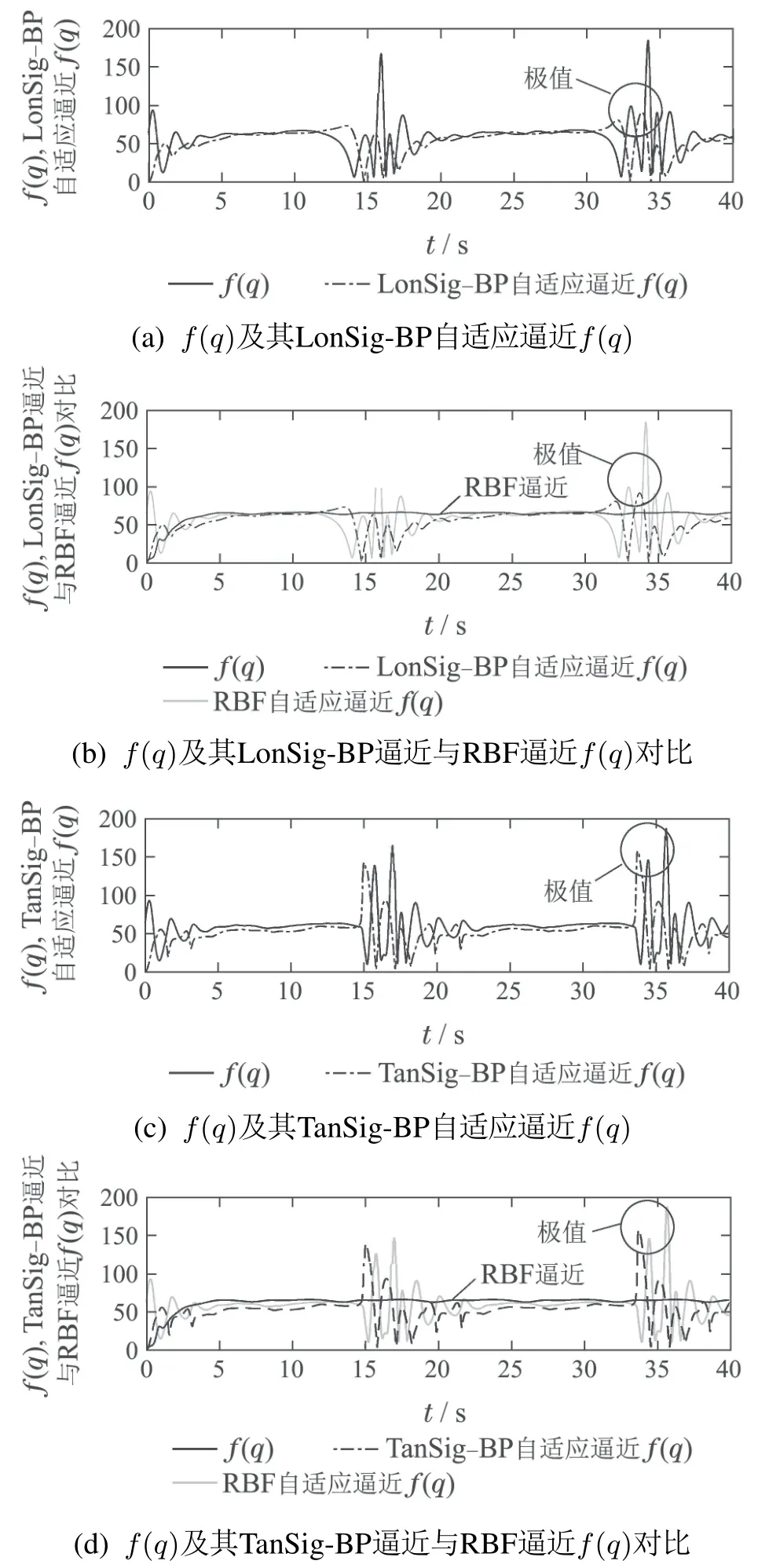
式中:M∈Rn为正定矩阵;Ax=b为等式约束,A∈Rm×n,b∈Rn; l ≥Ex ≥h 为不等式约束,E∈Rj×n,h∈Rl,l∈Rj,h∈Rj,m 式中:κ1,κ2为调节比例因子,0为零向量. 3)双二次型模型的求解. 根据其拉格朗日乘子法KKT条件[26],式(34)中不等式约束条件等价于l−Ex<0,Ex−h<0,则求解式(34)等价于求解 设存在饱和函数g(ρEx+µ),使得∃ρ>0,使得 令M为正定矩阵且矩阵A满秩,求解拉格朗日方程可得 由式(37)可知AM−1AT可逆,则rank(AM−1AT)=rank(A)且满秩.令 将式(39)代入饱和函数式(36)得 使用一层神经网络训练式(40)得关于µ的状态方程为 式中:ε为比例缩放因子,sigr定义为 式中:r∈R,0 注3如图6所示为y=x,y=sgn x,y=sigr(x),其中:r=0.1,0.2,0.4,0.6,0.8;sgn x意为符号函数.当x>0时,sgn x=1;当x=0时,sgn x=0;当x<0时,sgn x=−1. y=sigr(x)函数在0 图6 y=x,y=sgn x和y=sigr(x),r=0.1,0.2,0.4,0.6,0.8的对比Fig.6 Comparisons of y=x,y=sgn x and y=sigr(x),r=0.1,0.2,0.4,0.6,0.8 引理1[27]假设M∈Rn×n且M ≻0,A∈Rm×n(m 4)双二次型收敛性分析. 引理2[21]设ES1ET的最大及最小特征值分别为ε1,εq,式中:E∈Rj×n,S1=∈Rn×n.令 式 中:D=diag{d1,d2,···,dq}∈Rq×q且di∈R,0≥di≥1(i=1,2,···,q);I为适当维度的单位矩阵;ρ∈R,0 ≥ρ ≥2/εq,则 成立,并且x(A+AT)x=0,S1ETx=0成立.综上,当ε>0, 0 的解,则该神经网络收敛. 如果矩阵ES1ET满足满秩条件,则该神经网络会收敛,收敛时间不超过 二关节机械臂系统动力学方程为 式中:g=9.8为重力加速度;A=[a1a2a3a4a5a6],其值的大小是与臂长臂重有关的物理量,取A=[3.6 0.5 1.3 0.7 6.0 0.7];取自适应RBF网络中c,σ分别为 取自适应RBF网络输入θd为 则输入 系统广义节点位置实际坐标矢量θ初始值为随机生成, 此取θt=0=[0.2 0]T,则t=0=[−0.2 0]T;取自适应律因子Z=diag{z1,z2,···,zn}中z1=z2=···=zn=1.5,此处n=9,该值与c取值有关,控制律参数取 误差项s中取εN=0.2,εd=0.1,雅可比约束矩阵为 式中B=[b1b2]为与二杆机械臂臂长有关的物理量,取B=[1.0 1.2]. 在二次模型求解中,取κ1=1,κ2=1.6,取 取w1=w2=w3=1,取状态方程比例因子ε=10−9,r=0.8,ρ=0.03进行数值模拟仿真. 如图7所示为关节1和关节2的角度跟踪及角速度跟踪.初始阶段,随机初始状态角度及角速度产生了震荡状态,在本实例仿真中,产生较大扰动震幅的主要原因是RBF网络隐含节点的中心向量ci及标准化常数σi的取值相关联,而中心向量和标准化常数的取值及求解问题,目前作为一个困难问题[28],本文未对其展开讨论;随后阶段,当趋势趋于平稳状态时与理想值趋于吻合,验证了系统的稳定性.通过图8可以看出,其各参数、各维度趋于平稳状态时,其理想数值吻合度较好,再次验证了本文所述系统模型的稳定性. 图7 关节1及关节2的角度跟踪和角速度跟踪Fig.7 Position tracking and speed tracking for link 1 and 2 如图8所示为如式(2)所示机械臂动力学方程中W,C,G,Ff的理想状态下输入及如式(22)所示基于Gaussian的RBF网络自适应逼近输入数值跟踪曲线,通过如图9所示为关节1和关节2的动力学方程的控制输入,其曲线趋于平稳. 图8 动力学方程中W矩阵、C矩阵、G矩阵、Ff矩阵数值跟踪Fig.8 The numerical tracking of W matrix,C matrix,G matrix,Ffmatrix in kinetic equation 如图11所示,对于选取不同的激励函数所设计出的控制律有不同的自适应逼近性能,通过对比采用Sigmoid函数、Tan-Sigmoid函数及Gaussian函所设计出的控制器拟合曲线可知,采用Gaussian函数作为隐含层中激励函数的RBF网络具备收敛速度快、稳定性好、唯一逼近、无局部极小值等优点,可以实现快速学习并避免局部极小值等特性. 图9 关节1及关节2动力学控制输入Fig.9 Kinetic control input for link 1 and link 2 图10 f(q)跟踪及RBF自适应逼近Fig.10 f(q)tracking and RBF adaptive approximation 图11 基于Sigmoid函数、Tan-Sigmoid函数及Gaussian函数自适应逼近f(q)效果对比Fig.11 Comparison of the effect of adaptive approximation of f(q)based on Sigmoid function,Tan-Sigmoid function and Gaussian function 对于双二次型模型的性能指标泛函指标的求解,选取r=0.8,仿真时间为7×10−8s,µ0为随机输入,取 如图12所示,其数值在有限时间内稳定收敛,验证了所采用的新型类递归神经网络求解法能在求解双二次型泛函问题上具备较快的收敛速度;如图13所示,各项数值在有限时间趋于稳定,其数值仿真输出为 图12 双二次型泛函状态方程µ收敛时间Fig.12 Di-quadratic functional state equationµconvergence time 图13 双二次型性能泛函各项指标输出ë,u,λFig.13 Di-quadratic performance functional indicators output ë,u,λ 综上所得:求得其式(1)中最优跟踪误差和最优控制动作律分别为 即为式(1)所示待求参数,实现基于机械臂系统的最优控制. 通过数值模拟仿真验证了双二次型性能最优泛函本质:使用不大的控制量,来保持较小的控制误差,以达到所耗费的能量和控制误差的综合最优. 针对本文所提模型,主要从两大方面进行对比分析,其一:神经网络自适应逼近算法中激励函数的设计对比;其二:带约束条件的复合双二次型模型的解法对比. 1)激励方式从选取Gaussion函数(本文模型所提RBF网络)Sigmoid函数或Tan-Sigmoid函数(后两者称为BP网络)等方面在自适应性(收敛性)及其收敛时间、计算复杂度方面的对比如表1所示. 表1 激励函数模型各项指标对比Table 1 Comparison of indicators of excitation function model 2)对于带约束条件的复合双二次型模型的求解,对比现有求解模型在理论误差、空间复杂度及收敛时间等方面性能对比如表2所示. 表2 复合双二次型模型的求解各项指标对比Table 2 Comparison of index for solving composite bi-quadratic model 通过表1及表2在两个主要方面对比可知,本文所提模型在自适应性、收敛性及收敛时间、理论误差、计算复杂度及空间复杂度等方面性能得到改善,理论分析及数值仿真验证了本文所提模型. 本文针对非线性机械臂系统中权衡控制能量与控制误差比重的最优控制问题,通过以下3个方面出发进行讨论说明,即:1)保持跟踪误差趋于0值附近的跟踪问题;2)限制系统控制动作矢量达到降低系统实现代价的节能问题;3)设计自适应逼近控制律及优化复合双二次型求解模型,实现稳定快速收敛问题.针对以上3个方面,本文提出了一种基于神经网络二阶段叠加优化的双二次型最优泛函求解模型,实现在非线性机械臂控制系统中用不大的控制能量来保证较小的控制误差的综合最优控制.首先,设计一种线性误差函数,实现对非线性控制方程的控制,设计基于RBF网络以任意精度自适应逼近非线性方程,实现对非线性系统的最优控制;其次,设计复合双二次型模型,将待求参数复合成一个未知矢量,并设计一种新型的类递归神经网络求解带约束条件的双二次规划问题,实现模型求解的快速收敛;最后,通过理论分析及数值仿真验证了所提模型有效提高非线性系统的自适应性、控制精度、稳定性及鲁棒性等,实现非线性系统的综合最优控制.


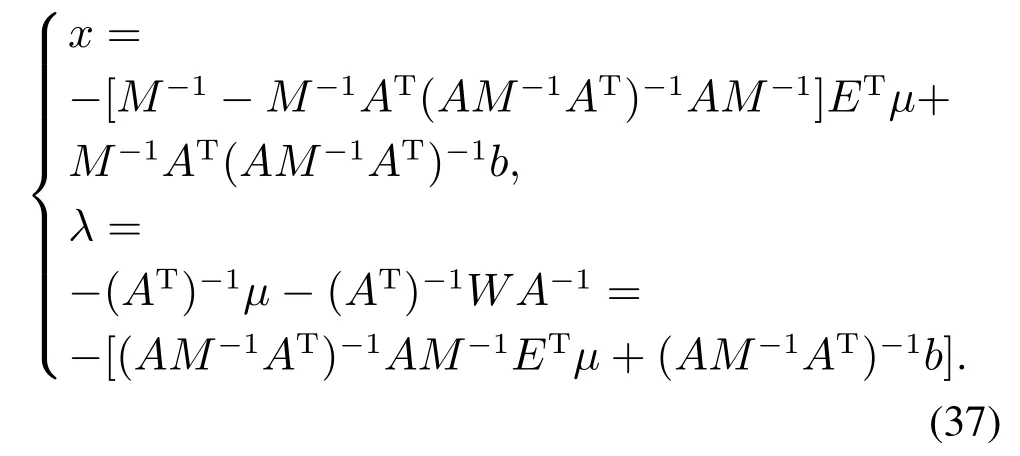
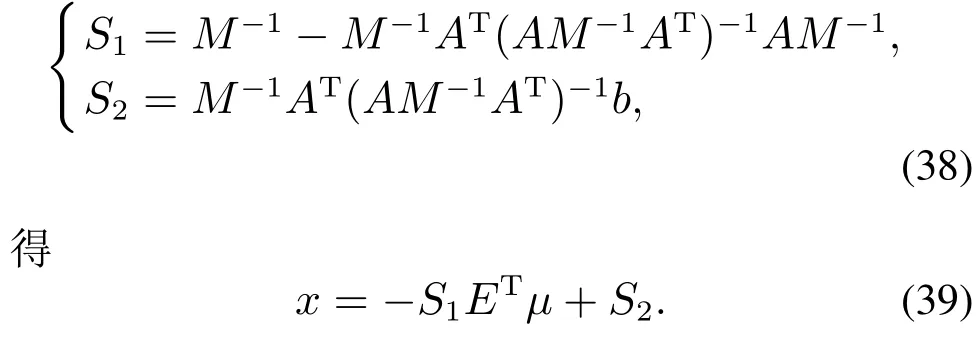

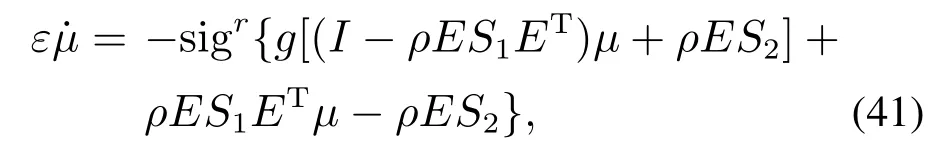



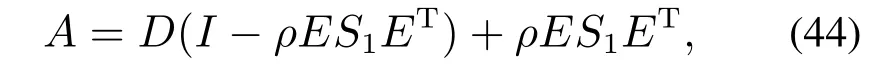

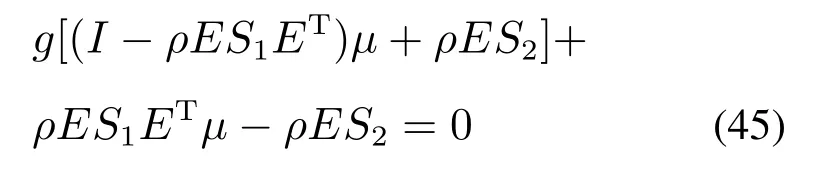

3 仿真实例与分析
3.1 仿真实例













3.2 比较分析


4 结论

