双层结构模型预测控制算法性能分析
孙浩杰 邹 涛李丽娟
(1.中国科学院沈阳自动化研究所中国科学院网络化控制系统重点实验室,辽宁沈阳 110016;2.中国科学院机器人与智能制造创新研究院,辽宁沈阳 110016;3.中国科学院大学,北京 100049;4.南京工业大学电气工程与控制科学学院,江苏南京 211816)
1 引言
模型预测控制(model predictive control,MPC)是先进过程控制策略的典型代表,自20世纪70年代中期提出以来,在工业过程诸多领域中得到成功应用[1],现已成为工业界最受认可的先进控制解决方案[2-3].
分层递阶结构优化控制是目前工业过程普遍采用的一种过程控制架构[4],MPC在该体系架构中位于核心部位.其上层为实时优化层(real time optimization,RTO),RTO面向全过程进行优化[5],为MPC提供外部目标(external target,ET);下层为基础控制层,一般为PID控制回路.中间层MPC采用集成稳态目标计算(steady state target calculation,SSTC)的双层结构MPC控制策略,由于稳态目标计算层通常利用线性规划(linear programming,LP)或二次规划(quadratic programming,QP)优化问题实现,一些文献中也将双层结构MPC称为LP-MPC或QP-MPC[6].
双层结构MPC在工程实践中的成功应用引起国内外学者的广泛关注并展开相关研究[7].在国内,邹涛等阐释了双层结构MPC在方系统与非方系统中解的相容性与唯一性问题[8],并提出双层结构MPC框架下含积分过程控制的解决策略[9-10].为双层结构模型预测控制的理论研究奠定了基础,在文献[11-12]中阐述了双层结构MPC策略在工业过程控制中的实现策略及应用优势.文献[13-15]将双层MPC算法推广至状态空间模型下进行阐述,对稳态目标计算层引入多优先级及约束可行性问题进行讨论,并详细描述了其在工程软件中的实现流程.以上研究大多针对双层结构MPC的基础理论算法与工程实施策略,缺乏针对双层结构MPC算法性能的系统分析与讨论.
Nikandrov等人[16]在假设稳态模型有偏差的情况下,分析了稳态目标计算层对于误差的灵敏性问题.Kassmann等人[17]针对模型不确定性研究稳态目标计算问题.Rao等人[18]针对带有可测噪声的线性时不变系统,采用无限时域二次性能指标,以综合方法为基本工具给出系统指数稳定性的结果.Maeder等人[19]在假设系统动态稳定性的前提下,对双层结构MPC的无静差性进行了分析.以上分析均在有条件假设的铺垫下得出研究结论,没有揭示双层结构MPC的实用价值及内在性能优势,从而阐明其被工业过程控制所青睐的原因.Ying等人[6]对双层结构MPC与常规MPC在稳定性、经济性等方面进行了分析比较,但在经济性及控制性能方面的分析较为笼统,本文将在其研究基础上作进一步深入分析.
众所周知,双层结构MPC的稳态目标计算层具有可行性判定及在优化问题不存在可行域时根据约束优先级等策略进行软约束调整的功能.本文在假定存在可行域的前提下,立足于分析增加稳态目标计算层对常规MPC算法在控制性能、经济性能、鲁棒性等方面的影响,从而阐明双层结构MPC相对于常规MPC的性能优势.内容安排如下:第2小节对双层结构MPC稳态目标计算层的不同功能模式分别进行简单介绍;第3小节从动态性能及稳态性能两方面讨论了稳态目标计算层对MPC控制性能方面的影响;第4小节分析了稳态目标计算层采用兼有跟踪控制及经济优化的性能指标,在满足对外部目标跟踪的同时利用操作自由度对部分关键经济变量进行优化来提升系统经济性能;第5小节简单分析了增加稳态目标计算层对系统鲁棒性的影响;第6小节是实验仿真部分,对所做分析进行一一验证.
2 稳态目标计算层算法描述
双层结构MPC在实时优化(RTO)层和常规MPC层中间增加了局部稳态目标计算层,其结构框架如图1所示,所增加的稳态目标计算层一方面可以对外部目标(上层实时优化器RTO给出或由操作人员设定)进行跟踪控制,另一方面也可以独立完成局部经济优化,并将优化结果传送至动态MPC作为设定值.下面将分别对双层结构MPC的稳态优化模型及稳态目标计算层所实现的不同功能进行描述.

图1 双层结构MPC结构框图Fig.1 The structure diagram of double-layered MPC
2.1 稳态优化模型
双层结构MPC上层稳态目标计算层采用MPC动态数学模型稳态增益作为稳态优化模型,在无不可测外部扰动的情况下,稳态优化模型可描述为

其中:Kssu,Kssf分别表示输入变量稳态增益矩阵和可测扰动变量稳态增益矩阵,yssT,ussT,fssT分别表示稳态输出、稳态输入和过程处于稳态时的可测扰动变量,essk为稳态预测误差修正项.由于实际应用中控制输入输出变量均以实际值形式出现,而式(1)中输入输出使用的是以稳态工作点为基点的相对值,则将式(1)进行变换如下增量形式作为稳态预测模型进行应用:

2.2 稳态目标计算模式
1)外部目标跟踪模式.
稳态目标计算层对外部目标进行跟踪可描述为一个QP问题如下:
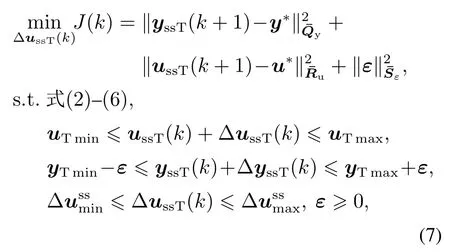
其中:(y∗,u∗)表示外部目标值;(y0,u0)为该目标函数在系统初始稳态(yssT,ussT)下寻找稳态工作点使之与(y∗,u∗)在最小二乘意义下距离最短;和分别为稳态输入输出目标权重系数矩阵;为放松因子权重系数矩阵;ε为输出约束放松因子;uTmin和uTmax分别为稳态输入变量的约束下界和约束上界;yTmin和yTmax分别为稳态输出变量的约束下界和约束上界;和为稳态输入增量约束下界和上界.
2)局部经济自优化模式.
稳态目标计算层可在MPC对应可行域内进行经济目标自优化,进而为下层MPC提供可靠的目标设定值,优化周期与动态MPC执行周期相同.该优化问题可被描述为如下线性规划问题(LP问题):

3)兼具目标跟踪及经济优化模式.
在以往对双层结构MPC算法的描述中[20-21],稳态目标计算层所包含性能指标函数只有式(7)-(8)所描述的两种形式,对于某些控制过程,若在优化指标中同时包含稳态跟踪型指标和经济优化指标,则能更大程度的体现双层结构MPC的优势.现将该类性能优化指标描述如下:

3 控制性能分析
双层结构MPC相较于常规MPC增加了稳态目标计算层,就对外部目标的跟踪实现来讲,双层结构MPC分两步进行:首先是在稳态目标计算层,从稳态可达的角度,在局部可行域内计算出理想的稳态目标值,然后传至动态层进行跟踪控制.这种分步操作不仅有利于稳态控制参数和动态控制参数的分别调节,而且可在工况改变时,首先从稳态控制角度进行调节和优化,有助于控制系统性能的提升.下面在不考虑控制参数影响的情况下,从动态性能及稳态性能两方面分析增加稳态目标计算层对系统性能的影响,为分析过程简单明了,本文以无约束MPC算法为基础进行分析,其结论可拓展至有约束的MPC算法中.
3.1 动态性能分析
假设一个包含m个控制输入和n个被控输出的多变量过程,控制时域为M,被控时域为P.为实现对输入输出目标[uT(k) wT(k)]的跟踪,动态层MPC在每个执行周期内优化如下性能指标:



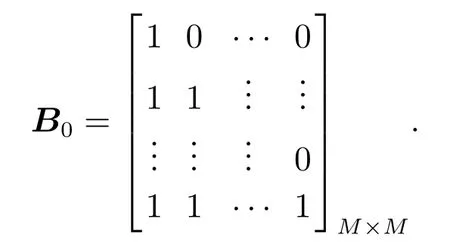
均为正定或半正定加权矩阵,A为模型动态矩阵.uM(k−1),∆uM(k),umin,umax,∆umin,∆umax均为mM ×1维向量矩阵,ymin,ymax为pP ×1维向量矩阵,B=block-diag{B0,···,B0},
在无约束情况下推导即时控制增量∆u(k)如下:
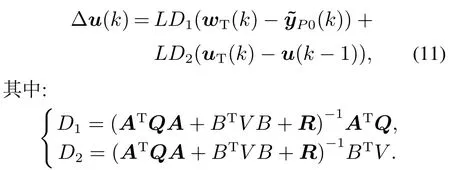
可一次离线计算得出

由上式可知,控制增量∆u(k)的计算依赖于跟踪目标[uT(k) wT(k)]的给定,常规单层MPC算法中,[uT(k) wT(k)]由RTO提供或人为给定,即
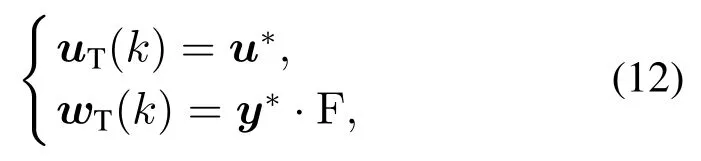
其中F为平滑滤波函数.在双层结构MPC中跟踪目标[uT(k) wT(k)]由稳态目标计算层给出:

下面在无约束情况下推导稳态目标计算层输入输出目标(ussT,yssT)的计算过程:

上式中矩阵均为常数矩阵,可转换表述如下:

其中:
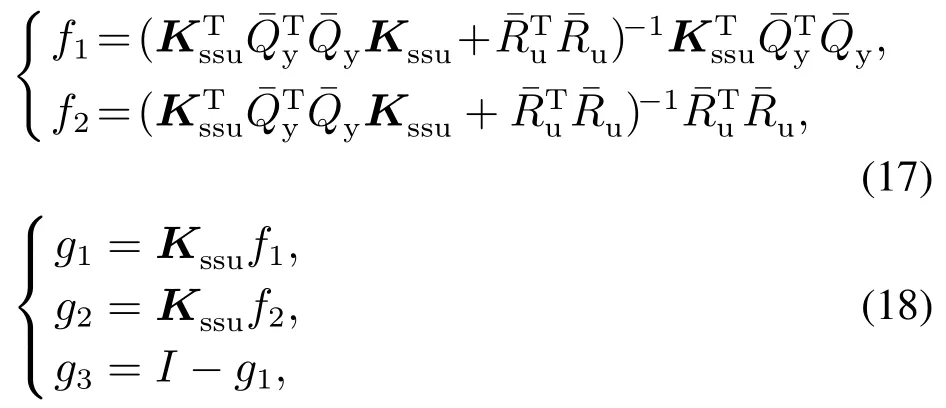
其中f1,f2,g1,g2,g3均为常数矩阵,由此可见,上层稳态目标计算层相当于一个前馈控制器.可优先综合考虑外部目标值和预测误差,为动态层提供设定值(ussT,yssT).由式(11)可知,动态层输入输出设定值更符合实际,则计算得到的控制量就更加合理.
基于以上分析,对于给定外部目标(u∗,y∗)的跟踪控制问题,可总结如下:i)若(u∗,y∗)在MPC可行域内且被控过程不存在扰动的情况下,双层结构MPC的稳态目标计算无须对跟踪目标进行调节,动态层参数设置相同的情况下二者动态跟踪性能并无区别;ii)当(u∗,y∗)不在其可行域内时,稳态目标计算层可对其进行调节,给出一个合理的最接近外部目标的设定值(ussT,yssT);iii)过程存在不可测扰动时,双层结构MPC可在考虑扰动影响下实时调节稳态目标值传至动态层,保证所提供的设定值为动态不确定性下的实时最优值.
相对于常规MPC,由于双层结构MPC可在外部给定目标不合理及存在过程不可测扰动的情况下实时给出实际最优的稳态设定值,故控制量给定更加合理,控制波动更小,具有更优的控制性能.
3.2 稳态性能分析
常规MPC控制策略包含对稳态输入目标进行跟踪时,在实际应用中常常出现稳态静差,其主要有两方面原因所致:一方面是因为外部目标值(u∗,y∗)不满足动态MPC层所采用的线性模型关系,系统在跟踪控制量u∗的同时不能同时满足对y∗的跟踪,最终输入输出变量将呈现稳态静差(与输入输出权重系数有关).另一方面,由于外部目标的更新周期与底层MPC的执行周期不在一个数量级,当被控对象工况发生变化,或被控过程中出现外部扰动时,实时最优操作点已发生改变,而动态MPC层始终跟踪原外部目标值,从而导致稳态静差.
相较而言,双层结构MPC在稳态目标计算层采用动态控制层的稳态模型作为其预测模型,且稳态目标计算层优化周期可与动态控制层执行周期一致,从而规避了常规MPC的以上两个缺陷,当外部目标给定不合理及被控过程存在恒值扰动时,双层结构MPC能够实现无静差控制,分析如下:
过程存在恒值扰动(如阶跃型扰动)时,稳态输出模型可表示为

其中:f表示过程的可测扰动变量,es表示由过程不可测扰动带来的模型误差,对模型精度进行补偿.
在底层MPC控制达到稳态时,其稳态目标函数可描述为

其中:

(yss,uss)表示被控过程达到稳态后的输出值与输入值,且满足关系式
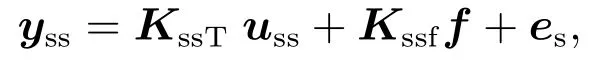
则当优化问题的解为yss=KssTussT+Kssff+es=yssT及uss=ussT时,使得目标函数Θ=0,满足优化解.由此可见,双层结构MPC对于恒值扰动可实现无静差控制.
4 利用操作自由度提升经济性能
与常规MPC相比,双层结构MPC的稳态目标计算层可在局部可行域内进行独立经济优化,直接考虑经济指标进行优化决策.此外,双层结构MPC稳态目标计算层还可采用包含目标跟踪和经济优化的性能指标,在保证对部分关键变量无静差跟踪的前提下,利用操作自由度对经济型关键变量进行优化,从而最大程度提升经济效益.
对于有m个输入变量和n个输出变量的多变量系统,稳态目标计算层在k时刻采用如下优化性能指标:

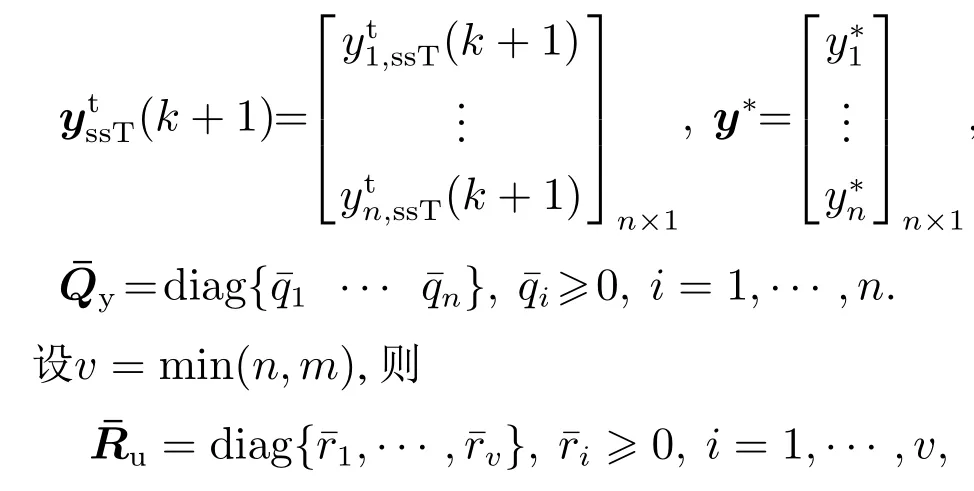

在不同优化条件下可分析如下:
情形1被控系统为方系统(n=m),输出变量约束均为等式约束:


由上可知,若实现对输出变量无静差跟踪,由于操作自由度缺失无法进行经济性优化,要获取更大的经济性能必然导致部分输出被控变量存在稳态静差.
情形2被控系统为胖系统(n 对于胖系统,对n个变量实现跟踪可能存在无数多个可行解,对m个操作变量经济性由低到高排序: 此时可优先选择经济代价小的前n个操作变量实现对输出变量进行跟踪,然后利用多余的m−n个操作自由度对经济性关键变量进行经济优化,从而实现更高的经济能效. 情形3对于方系统和瘦系统(n ≥m),假设前n′(n′ 上式中,∆yi,ss为允许控制裕度,输出权重系数设置为 被控变量区间约束使得操作变量有可操作空间,从而根据经济性对关键经济变量在满足被控变量区间的情况下进行优化,进而实现经济性能提高,这也是双层结构MPC最大的优势所在. 以2输入2输出的方系统为例,控制目标及可行域如图2所示,图中虚线v表示优化指标中对进行无静差跟踪,被控输出y2满足约束,同时经济型关键变量为u2,经济代价系数为正.即稳态目标计算层优化目标为在满足对被控输出y1实现跟踪的前提下,操作变量u2要求最大化以获取经济效益.图2中,虚线段中间位于阴影区域内的实线段表示在满足对输出y1实现无静差跟踪的前提下,经济型关键变量为u2的可优化自由度,通过优化得到实现最大经济效益的圆点SST. 图2 包含外部目标跟踪和经济优化示意图Fig.2 Schematic of include external target tracking and economic optimization 被控过程存在不可测扰动可视为扰动未建模引起的模型失配,所以模型失配及过程不可测扰动对控制系统的影响是相同的,均导致预测误差存在,预测误差超出可控范围即导致系统控制呈现稳态静差甚至不稳定现象.常规MPC算法具有反馈校正环节,可对一定程度模型失配进行补偿校正. 双层结构MPC不仅在动态控制层具有反馈校正环节,还具有稳态目标计算层的前馈调节功能,预测误差信息同时反馈至稳态目标计算层,利用反馈获得的预测误差信息对稳态优化目标进行再调节及再优化,从而使得双层结构MPC具有更强的抑制扰动和模型失配的能力.同于经济优化性能的提高,双层结构MPC鲁棒性的提高也依赖于可利用的优化自由度的大小,若无多余的操作自由度可利用,其鲁棒性能则同于常规MPC. 在此需要指出的是,限于所拥有可优化自由度的方向性,双层结构MPC相较于常规MPC只针对特定方向的扰动及特定通道的模型失配时具有更强的鲁棒性. 例如第6.3节的精馏塔实验模型中,在设定的控制目标下,双层结构MPC和常规MPC对扰动及模型失配的鲁棒性比较如表1和表2所示,即所构造控制环境下,双层结构MPC在输出端承受负向扰动和y2−u2通道增益减小时有更强的鲁棒性,反之则不存在明显优势.具体仿真分析在第6.3小节中阐述. 表1 双层MPC与常规MPC所能承受最大扰动幅值比较Table 1 Comparison of largest amplitude of disturbances double-layered MPC and single-layered MPC can handle 表2 双层MPC与常规MPC所能承受y2−u2通道最大增益失配比较Table 2 Comparison of maximum gain mismatch of of double-layered MPC and single-layered MPC can handle 以精馏塔woodbery模型为实验对象,这是一个典型的2输入2输出模型,过程模型如下: 其中:y1,y2为系统输出变量;u1,u2为输入控制变量;ld为过程不可测扰动变量;各变量满足如下约束条件: 控制量u1,u2约束: 控制增量∆u1,∆u2约束: 稳态增量∆uss1,∆uss2约束: 被控输出y1,y2软约束: 被控输出y1,y2硬约束: 不可测干扰数学模型: 控制器模型取标称模型,即Gc=GP,为比较双层结构MPC与常规MPC控制策略的控制性能,现假设分别利用这两种策略对RTO提供的被控输出目标进行跟踪:y∗=[−5;−10],设置稳态层和动态控制层输入输出权重系数: 在200 s ≥t ≥400 s时间段内在输出端加不可测扰动ld=2.两种控制策略的输入输出曲线如下图3所示,绿色点划线为给定的输入输出外部目标曲线,供双层结构MPC及常规MPC进行跟踪控制;红色虚线为双层结构MPC上层稳态目标计算层输出的稳态目标设定值曲线;黑色虚线为常规MPC的实际输入输出曲线;蓝色实线为双层结构MPC控制策略的实际输入输出曲线(各类型曲线代表意义在本文以下仿真中均相同). 由图3可以看出,在控制初始阶段(0 s≥t≥200 s),两种策略均可实现对输出设定点的无静差跟踪,双层结构MPC的稳态优化层无需对输入输出设定值进行调节,在控制参数设置相同的情况下,两种策略控制性能相同;当过程存在不可测扰动时(200 s 图3 双层结构MPC与单层MPC控制性能比较(r1=r2=1)Fig.3 Control performance comparison of double-layered MPC and single-layered MPC(r1=r2=1) 图3中,控制变量u1的曲线在t=200 s扰动出现时,初始动作方向与稳态时相反,其原因是输出响应由u1,u2共同决定,而控制量u2对输出的稳态增益较大,其较小的增量则引起较大的输出量变化,则需要u1对其产生的过量动作进行弥补.在此可通过输入变量权重系数设置或输入变量增量约束设置,限制控制变量u2的增量变化∆u2幅值,使得扰动产生时,控制变量u1的初始动作方向与稳态方向一致,通常以下两种方法实现: 方法1增大控制变量u2的权重系数: 方法2改变控制变量u2的增量约束: 采用方法1得到的输入输出曲线如图4所示,图中控制变量u2不再产生起始动作方向与稳态方向不一致的现象.如图3-4所示,控制参数改变后,对系统输入输出稳态值也有影响,存在过程扰动时,双层结构MPC的控制曲线u1,u2更加平稳. 图4 双层MPC与单层MPC控制性能比较(r2=200)Fig.4 Economic performance comparison of double-layered MPC and single-layered MPC(r2=200) 现假设在标称模型下,控制要求包含跟踪型目标和经济优化指标:在对输出变量y1进行跟踪的同时,使操作变量u2最小化来实现经济节能.t=200 s时,在输出端加不可测阶跃型扰动ld=−1.控制目标:y1=10,y2≥10,−2 ≥u1≥2.经济目标:min u2,set. 单层MPC依靠跟踪RTO提供的优化目标值来实现控制,由于RTO的优化周期较长(通常为小时级),为仿真效果在此假定其优化周期为400 s.双层MPC和单层MPC输入输出仿真曲线对比如图5所示. 图5 双层MPC与单层MPC经济性能比较Fig.5 Economic performance comparison of double-layered MPC and single-layered MPC 图5中,蓝色实线为双层MPC控制曲线,黑色虚线为单层MPC控制曲线,紫色点划线为输出变量y2的区间约束下限.从图中可得,当被控过程在t=200 s处有输出扰动时,双层MPC随即响应,在保证输出y1跟踪指标和满足y2约束时,使得经济变量u2更小,实现了经济节能.相反,单层MPC在扰动出现后始终保持对前一时刻设定值的跟踪,在RTO下个周期更新设定之后才实现经济最优化,与双层MPC相比,其对过程扰动的反应更慢,从而造成经济损失,如图中u2曲线构成的阴影区域为经济损失部分. 采用如上所述2输入2输出woodbery模型,控制目标与第6.2节中相同.下面分别单独考虑系统存在外部扰动和模型失配下的鲁棒性,即在分析二者对外部不可测扰动的承受能力时,控制器模型取标称模型;分析二者对模型失配程度的鲁棒性时,假设无外部不可测扰动影响. 由于对输出y2控制要求为满足区间约束,则对于该2输入2输出系统有一个自由度可以利用来应对外部不可测扰动和模型失配的发生.动态控制层取相同的控制参数:输出变量权系数:Q=[1 0;0 1],输入变量权系数:R=[1 0;0 1].在输出端加不可测扰动ld. t=200 s时,分别在输出端加ld=−3.2的不可测阶跃型扰动,t=400 s时,更新外部目标设定值.双层MPC和单层MPC的输入输出曲线如图6所示. 图6 双层MPC与单层MPC抗扰动性能比较Fig.6 Comparison of anti-disturbance performance of doublelayered MPC and single-layered MPC 由图6可知,在输出端添加ld=−3.2扰动时,对常规单层MPC策略,其可调节自由度已发挥至最大限度,若扰动幅值更大,则无法满足控制要求.然而双层结构MPC由于及时调整了稳态输入输出目标值,仍然有富余的操作自由度,可承受更大幅值的扰动影响,通过仿真实验可得:在该实验案例中,双层结构MPC最大可承受ld=−5的外部扰动.同理,对于模型失配情况,常规单层MPC可允许y2−u2通道模型增益失配至原增益的0.66倍,而双层结构MPC可允许其失配至原增益的0.5倍,仿真如图7所示.可得,双层结构MPC对于不可测扰动的抑制以及模型失配的鲁棒性要强于常规MPC. 图7 双层MPC与单层MPC抗模型增益失配能力比较Fig.7 Comparison the ability of double-layered MPC and single-layered MPC resistance to model gain mismatch 通过将双层结构MPC与常规MPC策略比较分析,阐明增加稳态目标计算层在系统控制性能、经济性能、鲁棒性方面的优势,稳态目标计算层相当于一个前馈控制器,不仅可对外部目标进行预先调节,在过程存在扰动或突发工况的情况下,也可根据反馈信息首先从稳态角度进行调整,为底层动态控制提供合理的跟踪目标值,有利于改善动态控制性能.另一方面,所增加稳态目标计算层可在满足对外部目标跟踪的前提下,利用多余的操作自由度进行经济优化,从而提高经济效益,且一定程度上有利于系统鲁棒性的提升.正是由于双层结构MPC在性能方面拥有诸多优势,故在主流的工业过程软件中被广泛采用.



5 利用操作自由度提高系统鲁棒性


6 仿真







6.1 控制性能仿真比较
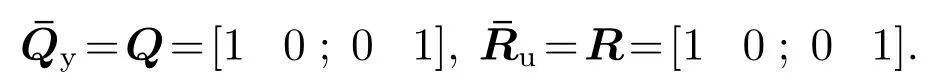





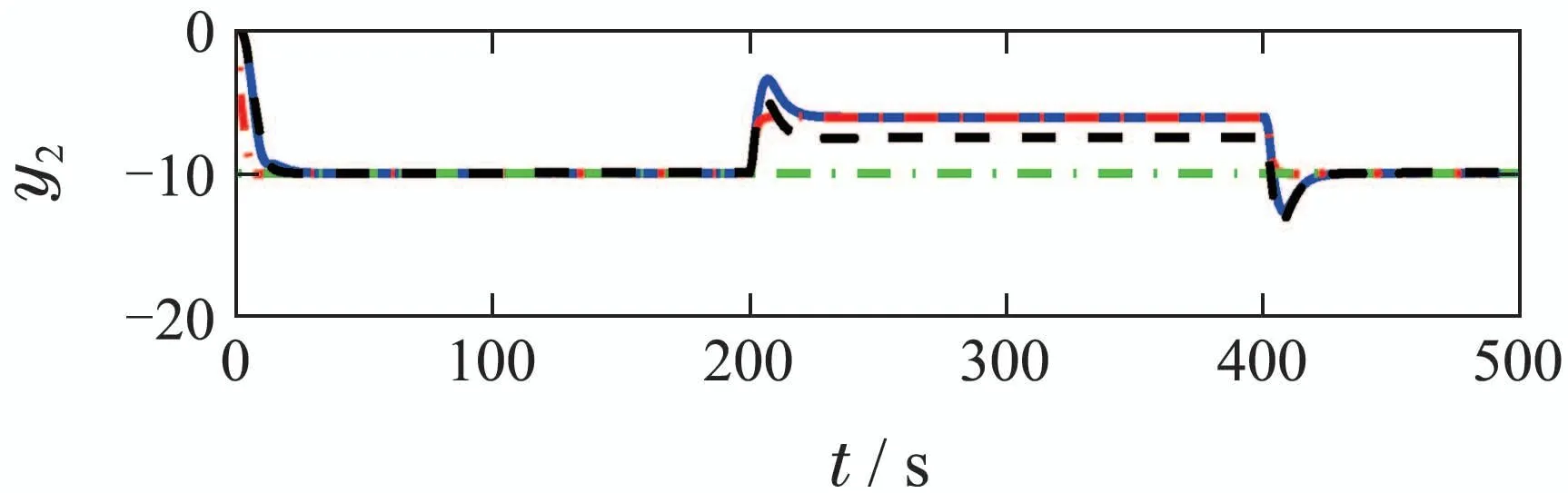
6.2 利用操作自由度提升系统经济性能仿真
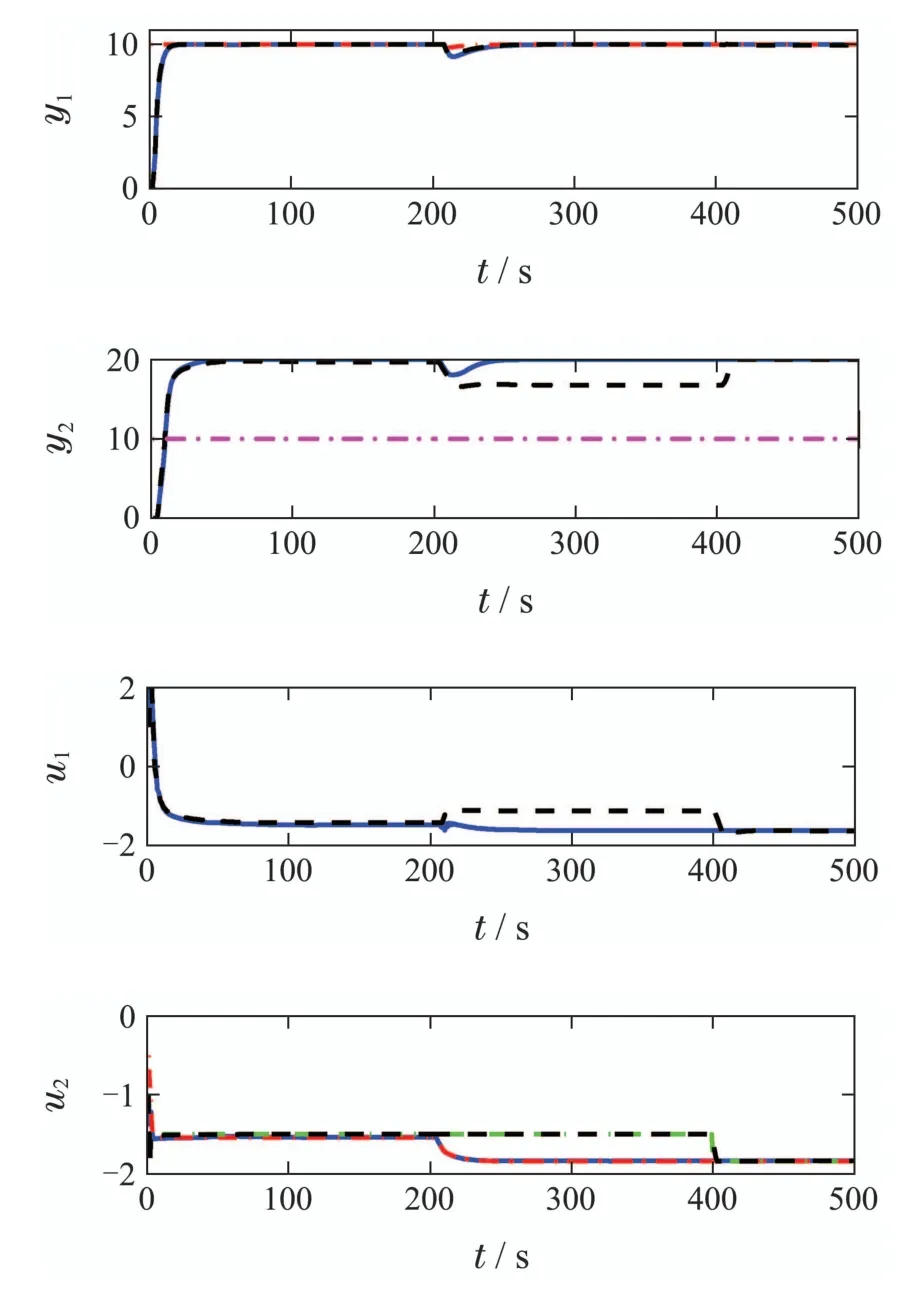
6.3 利用操作自由度提高系统鲁棒性仿真

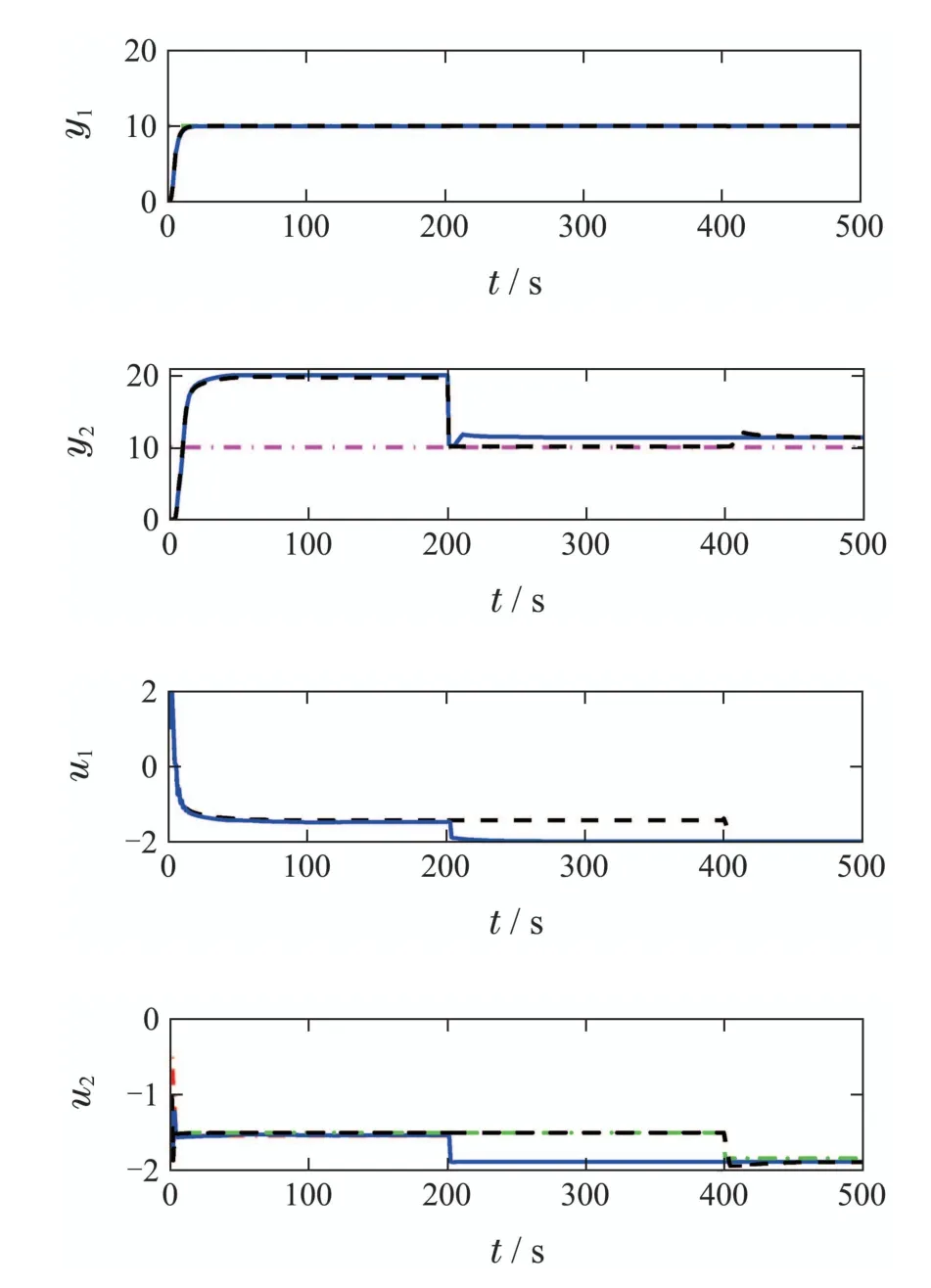
7 结论

