非线性系统有限时间控制研究综述
刘 洋 ,井元伟 ,刘晓平 ,李小华
(1.东北大学信息科学与工程学院,辽宁沈阳 110819;2.湖首大学工程学院,安大略桑德贝P7B 5E1;3.辽宁科技大学电子与信息工程学院,辽宁鞍山114051)
1 引言
针对某一系统进行控制器设计时,首要考虑的便是如何让其稳定地运行,换句话说,系统的稳定性是一切期望性能之基础.从20世纪中期至今,控制理论得到了空前的发展,涌现出大量可靠、优秀的控制方法,包括PID控制、极点配置、状态反馈、观测器、最优控制、模糊控制以及自适应控制等.这些方法均从不同的角度完善了控制理论,并解决了一些工程应用问题.然而,大部分已有设计方法,如PID控制和基于Lyapunov稳定性理论的方法却只能得到渐近稳定的结果,即只有当时间趋于无穷大时,系统的状态才能收敛到平衡点.但是,在诸多实际应用中,人们希望控制目标可尽快实现[1-2].比如当紧急情况发生时,汽车能够尽快停下来,从而降低人员伤亡;战争期间,若干个飞行器的编队作战或协同拦截,以便更快更精准地消灭敌机;在追击问题中,期望设计的导弹可以尽快跟踪并击中目标;亦或在实际生产过程中,商家希望在最短的时间内生产出更多的商品等等.而此时渐近稳定的结果无法满足人们的要求.于是,有限时间控制应运而生.
有限时间稳定性定义的雏形可回溯至1963年[2].但是,该技术的蓬勃发展是在20世纪90年代,主要源于有限时间李雅普诺夫理论[3]和齐次系统理论[4]的产生和完善.从那时起至今,非线性系统有限时间控制的研究已吸引了大批学者,并获得了丰硕的成果.因此,基于前辈们的优秀工作,本文将致力于尽可能详尽地总结和阐述非线性系统有限时间控制的发展情况.在给出具体非线性系统有限时间控制方法研究概述前,先将该领域涉及的一些定义和判据作简要的介绍.
符号说明:Ri代表i维欧式空间;如果A为一向量或矩阵,那么AT为A的转置,‖A‖为A的欧式范数;|x|为实数x的绝对值.
2 非线性系统有限时间稳定的定义、判据及设定时间表达式
为了后续内容叙述的方便,现给出两个非线性系统模型,分别为
其中:x(t)为系统的状态,f:D→Rn为非线性函数,d为外部扰动.
2.1 非线性系统有限时间稳定的定义
定义1[3-5]针对非线性系统(1),如果存在一个函数Tx(x0):Ω/{0}→(0,∞),使得对于任意的t∈[0,Tx(x0)],满足如下两个条件:
1)当t→Tx(x0)时,=0;
2)当t>Tx(x0)时,有x(t,x0)≡0.那么系统(1)是局部有限时间稳定的.若Ω=D=Rn,则系统为全局有限时间稳定的.
定义2[6-7]考虑非线性系统(2),如果存在ε>0和0 其中x(t0)=x0,那么,系统(2)是局部实际有限时间稳定的.若D=Rn,则系统为全局实际有限时间稳定的. 注1按照定义2的叙述,渐近稳定控制器,如u=−kx亦可得实际有限时间稳定的结果.但这样不仅无法显示带有幂指数参数的有限时间控制的优势,而且也会阻碍有限时间控制的进一步发展.为了区分有限时间有界(带幂指数的,如u=−)和渐近有界(如u=−kx)的不同,文献[8]给出了如下新的定义. 定义3[8]对于非线性系统(2),如果存在函数T(x0):Ω/{0}→(0,∞),f:D→Rn和一个正数△,使得,当t ≥T(x0)时,‖x‖<△,且系统(1)是有限时间稳定的,即满足定义1,那么,系统(2)称为局部有限时间收敛稳定.若Ω=D=Rn,则该系统为全局有限时间收敛稳定. 在上一小节中,已经给出了几个主要的非线性系统有限时间稳定的定义.本小节将总结非线性系统有限时间稳定或有限时间有界的判定方法. 引理1[3]考虑非线性系统(1),若存在一个C1函数V(x)>0,满足 其中:c>0,0<α<1,则系统是有限时间稳定的. 为了使系统状态收敛更快,给出如下引理: 引理2[9]对于一个非线性系统(1),若存在一个C1函数V(x)>0,使得 其中:c>0,b>0,0<α<1,则系统是有限时间稳定的. 不同于引理1和2,文献[10]给出一种较两者更快的充分条件,即引理3. 引理3[10]针对系统(1),若存在一个C1函数V(x)>0,使得 其中:c>0,b>0,0<α1<1,α2≥1,则系统是快速有限时间稳定的. 注2根据已有文献结果可知,采用引理2使系统(1)实现有限时间稳定所需时间要比引理1更短.具体的证明过程可以参见文献[11]的注2.1.同时,在文献[10]中也说明了引理2是引理3的一种特例,因为当α2=1 时,引理3就等价于引理2.而且,引理3可以使状态收敛的更快. 引理4[12]针对系统(1),如果存在正定且连续的函数V(x),使得 其中:c>0,b>0,0<α<1,则系统是有限时间稳定的. 注3引理4只能够说明在集合Φ内,系统的状态才能在有限时间收敛到平衡点,且Φ=因此,所得结果是局部的.在该引理的基础上,文献[8]给出了一个保守性更小的定理,即如下的扩展局部有限时间稳定. 引理5[8]针对系统(1),如果存在正定且连续的函数V(x),使得 其中:c>0,βi>0,0 引理6[7]针对系统(1),如果存在正定且连续的函数V(x),使得 其中:c>0,ϵ>0,0<α<1,则系统是实际有限时间稳定的. 引理7[13]针对系统(1),如果存在正定且连续的函数V(x),使得 其中:c>0,b>0,ϵ>0,0<α<1,则系统是快速实际有限时间稳定的. 本小节的工作是给出各类设定时间的显式表达,见表1-2. 表1 有限时间稳定的充分条件及设定时间Table 1 Sufficient condition of finite-time stability and its settling time 表2 实际有限时间稳定的充分条件及设定时间Table 2 Sufficient condition of practical finite-time stability and its settling time 表1-2中:T3i的表达式见注4,而Tj1(j=1,2,4,5,6,7)分别为 注4这里将给出表1中设定时间T3i的形式.当i=1且α2>1时,有 当i=2且α2=1时,有T32=T21. 注5表1和表2中的参数选择可参见第2.2节.两个表中已经给出了有限时间控制中常用的设定时间的形式.但是,仍有两种比较重要的形式没有提及.一种叫做固定时间控制,其收敛时间表达式可见第3.4.1节;另一种称为预设有限时间控制[14-16],其设定时间可以任意设置,不仅与初始条件无关,而且与设计参数也无关. 本节根据控制信号的连续性,将非线性系统有限时间控制方法分为如下几类:连续有限时间控制、不连续有限时间控制、光滑有限时间控制和其他经典有限时间控制方法,并逐一进行概述. 利用增加幂次积分技术和齐次系统理论得到的有限时间控制器是连续的,关于它们的研究进展将通过下面两小节来具体叙述. 3.1.1 基于增加幂次积分的有限时间研究概述 增加幂次积分(adding a power integrator,AAPI)是连续非光滑控制中一种十分有效的方法,由于其具有较好的抗扰性且可实现全局收敛,一直受到大量学者的关注.Lin等人在文献[17-19]中多次利用该技术,并得到了若干渐近稳定的结果.直到2005年,文献[20]第一次利用增加幂次积分AAPI技术,解决了n维非线性系统全局有限时间镇定问题.因为该技术中既不存在基于齐次系统理论的局限性(这里主要指无法处理扰动系统且不能给出收敛时间表达式),又可以避免终端滑模方法的奇异和抖震问题,同时可以显式地给出收敛时间的上界.因此,基于AAPI的有限时间控制方法,一经提出便引起了学者们的广泛关注.目前,针对各类非线性系统,已存在了大量的结果. 与文献[20]不同,文献[21]首次针对上三角非线性系统,采用top-down和bottom-up技术[22],解决了全局有限时间控制问题.到目前为止,可能由于处理上三角系统较为困难,导致此类系统的有限时间控制结果并不是很多[23-24].在上述文献的基础上,文献[25]和文献[10,26-31]研究了一类更一般的非线性系统的有限时间控制问题,这类系统被称为p--规范型系统,可表示成 在实际应用中,存在这样一类情况,即动态系统的运动方向是未知的,也可以称为控制增益/方向未知,比如吸气式高超声速飞行器的姿态控制[36]、船舶的航向控制[37]或者多智能体的编队[38]等,这给系统的设计带来了巨大的困难.在文献[39]中,Nussbaum提出了一种利用其名字命名的函数,即Nussbaum增益函数,解决了此问题.随后,涌现出大量关于未知控制方向的结果[40-42],但结论均为渐近有界的.文献[43]首次考虑了此类系统的全局有限时间镇定问题,设计了一个基于Lyapunov函数的逻辑切换规则,从而克服了未知增益带来的设计困难,并使系统的状态在有限时间收敛到零. 近年来,学者们提出了一些新的有限时间控制结果.在文献[44]中,作者设计了一个新的有限时间控制器,系统的状态不仅是有限时间稳定的,而且可以通过调节参数c的值,来获得期望的收敛速率和收敛时间.文献[45]给出了一种新的有限时间观测器的设计方法.除此之外,采用增加幂次积分技术,诸多非线性系统的有限时间控制问题得到了解决,如随机非线性系 统[46-47]、纯反馈非线性系统[48-49]、非完整系统[50-51]、非线性切换系统[52-53]以及非线性互联大系统[54]等.由于有限时间具有较强的抗扰性、较快的收敛速度以及较高的控制精度,所以在实际系统中同样存在大量的应用,如飞行器的姿态同步[55-56]、气味源定位[57]、四轴飞行器的空中悬停控制[58]、四轮汽车控制[59]、汽车机器人[60]以及电车爆胎控制[61]等. 以上提及的研究大都是假设系统的状态是完全可测的,但工程实践中往往系统的部分状态或全部状态不可测.这时上述设计方法将不可利用,需借助动态输出反馈控制来完成相应的控制器设计.文献[62-63]分别考虑了一个二阶系统和一类连续但非光滑的非线性系统全局有限时间输出反馈控制,这也是较早的研究结果.文献[12]针对一类非线性系统,设计了一个高增益观测器,并提出了一个局部有限时间稳定的引理.文献[64]针对一类主从混沌系统,给出了全局有限时间同步的控制方法.在每一个智能体的速度均不可测的情况下,文献[65]运用动态输出反馈方法,解决了多智能体系统有限时间编队问题.针对高阶前馈系统,作者凭借增加幂次积分和齐次占优方法,探究了其有限时间输出反馈镇定问题[66].当然,除了上述给出的增加幂次积分输出反馈的成果外,仍有大量的结果是关于非线性系统有限时间观测器的设计.尽管有一些结果是运用增加幂次积分的方法,但是观测器却为齐次观测器,亦或是终端滑模观测器.为了使本文的叙述更加清晰,这部分结果将会在后文的第3.1.2节和第3.2节中进行详细地阐述. 3.1.2 基于齐次系统理论的有限时间研究概述 相较于增加幂次积分方法而言,利用齐次理论实现非线性系统有限时间控制的过程更简便,所得控制器的形式也更简单.文献[4]最早给出了齐次有限时间稳定的结论,这里简述为,齐次系统是有限时间稳定的,当且仅当该系统是渐近稳定的并且具有负齐次度.该理论的提出为齐次有限时间控制的研究奠定了基础.然而,该技术却对非齐次系统的控制器设计无能为力.因此,文献[67-68]提出了一个新的定理,即若一个非齐次系统可以被分解成一个齐次系统和一个非齐次项,并且非齐次系统、齐次系统及非齐次项分别满足渐近稳定、有限时间稳定和特定约束,则该非齐次系统是有限时间稳定的.这一结论被文献[8]称为扩展齐次定理.但是,上述的两个重要结论无法显式地给出收敛时间上界的表达式.于是,经过该研究领域学者的努力,文献[69-70]揭示了基于李雅普诺夫理论与齐次系统理论的有限时间控制间的联系,可概括成,若齐次系统是有限时间稳定的,则≥−cV(µ+υ)µ,其中:V 是一个C1李氏函数,µ是函数V 的齐次度,υ 是系统的齐次度,c>0是一个常数,这样便可计算出收敛时间的上界.该定理通常被称为齐次反推定理[8].后续的研究工作几乎均是依赖上述3个重要定理.在文献[4]的基础上,文献[71]研究了齐次切换系统的有限时间稳定性.根据文献[69-70]的设计思想,文献[72]考虑了一类齐次随机非线性系统的有限时间稳定性问题.在无向拓扑的情况下,文献[73]利用齐次有限时间控制方法,为多智能体系统设计了一个分布式跟踪协议,以确保所有智能体可在有限时间被同时镇定. 另外,在许多实际系统中,该方法也得到了一定的应用.针对一个具有二自由度的机械手臂系统,文献[74]提出了比例-微分加(proportion differential+,PD+)的全局有限时间跟踪控制方法.在文献[74]的基础上,作者考虑了机械臂系统执行器受限的情况,进一步给出了齐次饱和控制器的设计方案[75].再进一步,文献[76]致力于研究多机械臂的协同控制,通过齐次理论,使得全部机械臂在有限时间收敛到目标位置.在小行星中心极坐标系下,文献[77-78]研究了探测器软着陆的齐次有限时间控制问题.文献[79]则探究了直流-直流变频器系统的有限时间自适应稳压控制.齐次有限时间稳定成立的前提,是存在一个精确描述的系统模型,否则无法计算系统的齐次度,这使得该方法具有一定的局限性.文献[80]虽然考虑了系统的外界扰动和参数不确定性,但是需要假设其随着系统的收敛最终衰减到零,这对扰动和不确定的限制较大. 同样地,上述结果只考虑了状态反馈的情况.接下来,本文将分析利用齐次理论设计有限时间输出反馈控制器的结果.文献[67]针对双积分器系统,首次提出了一种结构简单的齐次观测器的设计方法.通过与前文介绍的扩展齐次定理相结合,其应用范围变得更加广泛[81-83].其中,沈艳军等人提出了一系列相关结果[9,12,84-86].文献[12]第一次根据齐次反推定理给出了有限时间观测器的设计过程,并得出结论:如果非线性系统满足一致可观测和全局李普希茨条件,那么对于该系统存在半全局有限时间观测器.此后,通过引入一个观测器增益适应律,文献[9,84]提出了一个全局的有限时间观测器设计方法.文献[85]进一步将单输出的结果[9,12,84]扩展到了多输出的情况.而文献[86]则提出了一个新的增益适应律.此外,文献[87]考虑了一类时变非线性系统的有限时间观测器设计问题.根据文献[8]可知,齐次观测器和齐次反推观测器尽管形式大致一样,但对于非线性项的处理,后者具有较小的保守性,具体分析可见文献[8].基于齐次理论的输出反馈技术也在很多实际模型中得到了应用,如飞行器姿态协同设计[88]、感应电机直接转矩控制[89]、无摩擦的机械系统控制[90]等. 目前,应用最为广泛的一种控制信号不连续的有限时间控制方法为终端滑模控制(terminal sliding mode control,TSMC)技术.因此,本小节将对其研究状况展开论述.在介绍TSMC方法之前,不得不提及滑模控制(sliding mode control,SMC),这是一种十分有效的非线性系统控制策略.设计过程主要分成两个部分[91],第1部分为滑模面设计,第2部分则为控制律设计.然而,利用传统的线性滑模面,系统状态的收敛速率最快为指数形式,无法实现有限时间收敛.于是,文献[92-93]率先提出了TSMC方法.但是,早期的TSMC研究[92-95]主要存在两个缺陷:一是当系统的状态远离平衡点时,TSMC反而比SMC收敛更慢;二是存在奇异问题,即会产生无界的控制输入.为了解决这两个问题,文献[96]结合TSMC的优势和传统线性滑模面的设计想法,提出了快速TSMC 技术(fast-TSMC,FTSMC),以此来解决第一个问题.文献[97]则提出了非奇异终端滑模控制(nonsingular-TSMC,NTSMC)来解决第2个问题.由于文献[93,96-97]均属于不连续控制,易造成系统的抖震,这是实际中不期望发生的.为了减少或消除抖动,方法1是利用边界层(boundary layer,BL)方法来替换符号函数或正弦函数,但根据文献[98-99]可知,BL技术易产生较大的稳态误差且有限时间稳定性将缺失;方法2是在研究机械臂轨迹跟踪时,提出了一种连续的TSMC 设计方案[100];方法3则采用高阶滑模技术[101-103]. 近几年,终端滑模控制也有了一些新的进展.针对具有时变不确定的二阶非线性系统,文献[104]结合全局滑动面(global sliding surface,GSS),给出了一个新的FTSMC方法.文献[105]研究了一类非线性分数阶系统的自适应有限时间输出反馈控制器设计问题.同时考虑NTSMC和固定时间扰动观测器两种技术,文献[106]提出了一个适合二阶不确定系统的复合鲁棒控制方法.文献[107]讨论了非线性非仿射系统的非奇异快速终端滑模控制(NFTSMC)问题,运用泰勒级数展开,将非仿射结构转化为仿射形式,这简化了后续控制器和扰动观测器的设计过程.文献[108]以一个新的视角设计了NTSM控制器,使得系统的状态是全局固定时间稳定的.在文献[109]中,作者给出了一个更灵活的自适应全局终端滑模控制器设计方法,设计的两个自适应律分别用来估计不确定项和扰动的上界.针对离散系统,综合Grunwald-Letnikov分数阶定义和TSMC方法,文献[110]设计了一个高跟踪精度的分数阶终端滑模控制器.文献[111]指出,在缺乏状态信息时,同时使用积分链微分器和微分进化优化算法,可以取消参数估计的约束.基于此,该文提出了一种非线性系统的FTSMC方法.此外,许多高阶滑模控制器也可以实现有限时间控制目标[112-114].类似地,终端滑模控制也被用来解决大量的实际问题,比如六足行走机器人的姿态控制[115]、永磁同步电动机速度跟踪控制[116]、全电刹车系统控制[117]、Van der Pol混沌振荡器同步控制[118]、机械系统快速有限时间控制[119]等. 前两小节涉及的控制器均为非光滑的.目前,有关光滑有限时间控制的结果却很少,基本可以归结成两类:一类是通过速度转换,另一类是基于状态约束的思想.两种控制方法的优势不仅在于实现了控制器的光滑性,而且系统状态的收敛时间可以提前设置,与初始条件和设计参数均无关.此外,与第3.1节和第3.2节不同,本节介绍的有限时间稳定的充分条件将不再依赖“≥−cVα”,“≥−cVα−bV”或“≥−cVα+bV”等充分条件,其中:c>0,b>0 且0<α<1.接下来,将具体给出两种光滑有限时间控制方法的研究现状. 3.3.1 速度转换有限时间控制 该控制思想是在2016年由重庆大学宋永端团队率先提出[14],其基本设计思路可概括为:系统变换,即找到一个在期望时间可以增长到无穷大的时变函数,利用该函数将所研究系统转换成一个新系统.若能求证新系统是输入-状态-稳定的(input-state-stability,ISS),则可知原系统为有限时间ISS的.因此,原系统的状态可在预设时间收敛到原点.这里的转换函数为 其中:T代表期望的收敛时间,n和m ≥1分别为系统维数和一个常数. 文献[15,120]将文献[14]的方法应用到了高阶多智能体一致性控制研究中.在文献[121]中,作者详细比较了传统有限时间控制(带幂次的反馈)和速度转换有限时间控制,对比内容主要包括控制结构、收敛时间、抗扰性等.基于文献[14]的想法,文献[122]针对非完整非线性系统,设计了一个有限时间输出反馈控制器.目前,关于此类方法的研究成果并不是很多,但由于其设计简单及上述优势,未来的相关研究可能会越来越多.但此类设计方法只反映了系统状态从初始时刻到期望时刻T的动态变化,时间T之后的运动情况无法获知,这仅对于一部分实际问题可行,如导弹击毁目标的行为等. 3.3.2 状态约束有限时间控制 文献[16,123-124]提出了另一类光滑的有限时间控制方法,其基本思想主要受约束控制方法的启发.简述为,设计一个可在有限时间到达预先设定的任意小邻域的时变函数,结合一个单调递增且有界的误差转换函数或barrier Lyapunov函数,便可保证系统的状态、输出或跟踪误差在指定时间收敛到提前设计好的区域内.文献[16,123-124]给出了两个不同的时变函数,分别为 其中:ρ0,ρTf,λ和τ是正的设计参数;τ=∈(0,1],p和q分别是正奇数和正偶数;,υTf>0,预设的有限时间是Tf. 与速度转换方法不同的是,基于约束思想的控制策略考虑了整个时间轴的系统状态的变化情况.目前,采用此方法完成有限时间控制的结果并不多.然而,因其设计简单且易于实现,未来也许会有更多的成果涌现. 除了第3.1∼3.3小节介绍的3类主要有限时间控制方法外,本小节将介绍另外两个较为经典的研究成果,一个是固定时间控制,另一个则是实际有限时间控制(亦可称为有限时间有界). 3.4.1 固定时间控制 第3.1节和第3.2节中描述的传统有限时间控制方法,其设定时间函数受系统初始状态影响,从某种程度上说,这阻碍了该方法的实际应用,因为并不是每个实际系统的初始状态都可以提前获悉.幸运地是,文献[125]给出了一种新的设计方法,可称为固定时间控制,其定义为 定义4[125]系统(1),x(0)=x0,可称为固定时间稳定的,如果该系统是有限时间稳定的且设定时间函数T(x0)是有界的,即T(x0)≥Tmax. 由上述定义可知,固定时间控制的优势在于设定时间上界与初始条件无关,只与设计参数相关.到目前为止,文献[125-129]分别给出了几种判据及相应的固定时间表达式,可用引理8-11表示.为表述方便,现定义一个连续正定且径向无界的函数[126]V(x):Rℓ→R+∪0.接下来,引理8-11中的V(x)如上所述,且考虑的非线性系统为(1)所示. 引理8[125]如果存在一个函数V(x),使得 其中:α>0,β >0,p>0,q >0,k >0,pk <1,qk>1,那么,系统的原点是固定时间稳定的,且设定时间可由下式估计,即 引理9[127]如果存在一个函数V(x),使得 引理10[128]如果存在一个函数V(x),使得 其中:α>0,β >0,q >p>0且p和q均为奇整数,那么,系统的原点是固定时间稳定的,且设定时间为 引理11[129]如果存在一个函数V(x),使得 其中:α>0,β >0,q >p>0,m>n>0且p,q,m和n均为奇整数,那么,系统的原点是固定时间稳定的,且设定时间为 目前,绝大部分固定时间控制的结果均基于上述引理.最近,文献[130]首次针对高阶系统提出了固定时间稳定的控制方法.此外,许多实际问题也考虑了运用固定时间控制,如多智能体系统的一致性[128-129]、刚体飞行器姿态控制[131]、超音速滑翔车容错控制[132]以及高超声速导弹控制[133]. 3.4.2 实际有限时间控制 尽管之前的文献中也有一些有限时间有界的结果,但本小节的实际有限时间控制并不是基于上述的增加幂次积分、齐次理论或终端滑模等控制方法实现的.文献[6]首次给出了实际有限时间稳定的概念和充分条件.随后,青岛大学陈兵等做出了一系列成果.文献[7]结合模糊逼近技术和自适应控制,解决了严格反馈非线性系统有限时间控制问题.而且文中给出了一个引理,利用该引理可以实现半全局实际有限时间稳定的结果.之后,该方法被进一步应用到了非严格反馈系统[134]、非线性纯反馈系统[135]、非线性切换系统[136]等.在这些方法中,虽然模糊逻辑系统和神经网络可以逼近虚拟控制律及其各阶导数,但前提是这些导数应存在.然而,文献[7]和文献[134-136]的虚拟信号均为类似于如下形式的函数: 其中:i=1,2,···,n,0.5<γ <1,其他参数意义见文献[7]. 由γ的取值可以算出0<2γ−1<1,那么,微分αi时便会引起奇异问题,这是此类方法存在的一个问题.为了避免奇异问题的产生,文献[13]采用指令滤波技术,提出了一个快速实际有限时间控制算法.文献[137-138]继续用该方法分别解决了感应电机和飞行器姿态的有限时间控制问题.在全状态约束和存在死区的情况下,文献[139]研究了参数严反馈系统的自适应有限时间控制器设计方法.近些年,辽宁工业大学佟绍成团队也做出了一些结果[140-143].对于多输入多输出随机非线性系统,文献[140]提出了一个新的随机有限时间稳定性定理.文献[141]利用动态面控制处理了backstepping技术中计算复杂性问题,并考虑了多输入多输出非严格反馈系统的有限时间输出控制问题.文献[142]讨论了非线性开关系统的自适应神经网络有限时间容错控制器设计问题.文献[143]则研究了非线性互联大系统分散有限时间滤波器的设计.文献[144]利用积分滑模技术,实现了航天器姿态的有限时间容错控制. 注6齐次有限时间控制方法需构建一个完全已知的系统模型.即便是可以运用齐次扩展定理,但需要满足的条件太严苛.终端滑模有限时间控制则存在奇异问题和易产生抖震现象.相比之下,由于增加幂次积分有限时间技术不会产生上述问题,许多高阶和具有不确定项的系统,通常采用该技术.然而,增加幂次积分的问题在于设计过程十分复杂,需要进行大量的不等式缩放,导致控制输入幅度较大,所以不适合实际应用.因此,需设计更为简单的方法,如速度转换和约束类方法.固定时间虽说和初始状态无关,但此处的无关只是体现在收敛时间的上界与初始值无关,真实的收敛时间仍受初始状态的影响且控制增益较大.综上所述,在未来,控制器光滑的有限时间控制方法也许会得到较大的发展空间,因为其具有设计简单、控制律光滑、收敛时间可提前设定且与初始条件和设计参数均无关等优点. 本文针对当前的热点问题,即非线性系统有限时间控制,从研究背景、基本定义、判定方法以及研究现状等方面,较为系统地介绍了其发展情况.尽管近些年涌现了大量研究成果,但仍有许多相关控制问题未能深入研究,主要包括以下几方面: 1)基于观测器的非线性系统预设有限时间控制问题. 利用文中所提的性能函数或改进BLF函数,研究有限时间输出反馈控制问题.因为许多情况下,系统状态不能完全量测,此时需要借助全维或者降维观测器来解决相应的控制问题.因此,设计这样的控制器具有一定的理论和实际意义. 2)非线性离散系统的有限时间控制问题. 据作者所知,目前关于非线性离散系统的有限时间控制问题还没有结果呈现.这里主要是指没有类似于连续系统中≥−cVα的充分条件.随着数字控制理论的不断发展,许多控制问题的实现可转化成离散时间控制问题.因此,这方面的研究十分重要. 3)非线性扩展结构大系统的有限时间控制问题. 扩展结构大系统,简言之,在互联大系统中逐渐增加新的子系统后构造成的新的大系统.它可以用来模拟很多生物界和工业界的情形,比如电力系统扩容问题或者人体植入新的器官等.但是,目前关于此类系统的控制多集中在线性系统中,非线性的结果很少.因此,有必要在该领域做更进一步的探索. 4)非线性系统有限时间控制方法的实际应用. 大家知道,很多时候理论和工程实际是相互矛盾的,在理论上得出的完美结果,对于工程实际几乎没什么用,这是理论联系实际当中一直亟需解决的问题.在未来,如何利用有限时间控制方法来解决实际生产中的问题,有待于下一步的考察和研究. 除上述内容外,有一开放问题值得探究,如下: 5)探究收敛更快的有限时间控制方法. i)文献[3,10-11]分别给出了3个不同的有限时间稳定的充分条件(见引理1-3),现简写为 其中:c>0,b>0,0<α1<1,α2≥1. 受上述文献启发,如果设计一个函数V(x),使其满足 其中:m>0,α2=1且α3>1,那么是否可得到较文献[3,10-11]更快的收敛时间? ii)速度转换和状态约束两种有限时间控制技术可以使得收敛时间设计较为灵活,但速度转换只能实现[0,T]时间段的状态控制,状态约束只能得到有限时间有界的结果.因此,是否可以寻求一种新的控制方法,其可在整个时间轴内,使得闭环系统信号在有限时间收敛到平衡点且设定时间亦与初始条件和设计参数均无关? 6)此外,仍有一些问题有待解决,例如:如何找到更简单的李雅普诺夫函数的构造方法? 时滞/随机系统有限时间方面结果很少,主要在于李亚普诺夫函数的构造,这亦是未来需探究的方向.
2.2 非线性系统有限时间稳定的判据






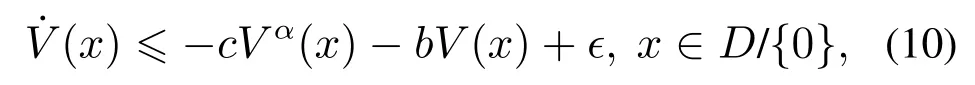
2.3 设定时间表达式


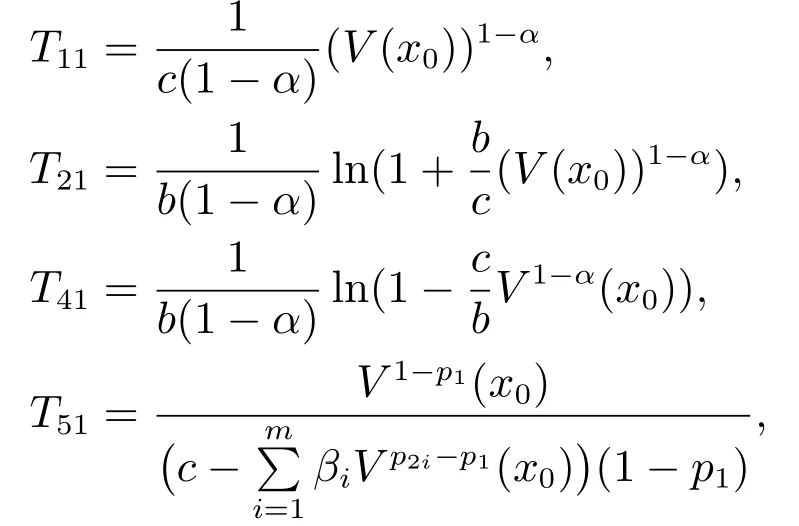
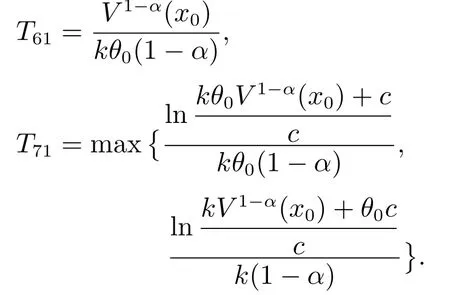
3 非线性系统有限时间控制的研究概述
3.1 控制信号连续的有限时间研究概述
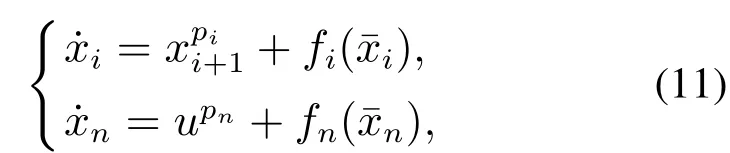
3.2 控制信号不连续的有限时间研究概述
3.3 控制信号光滑的有限时间研究概述

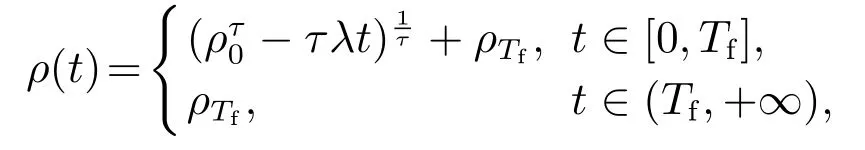

3.4 其他经典的有限时间研究概述
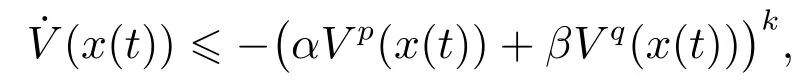
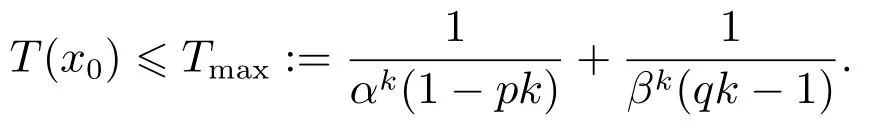
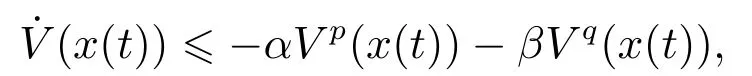



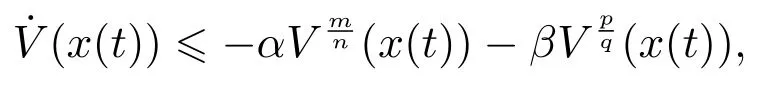
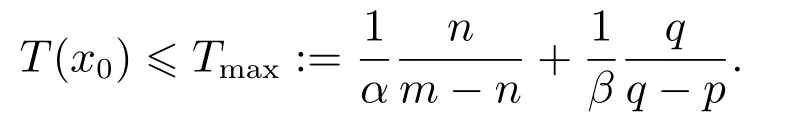

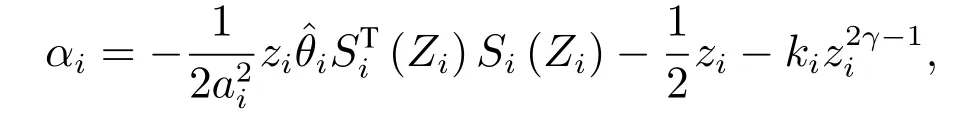
4 结论