推力矢量垂直短距飞机轨迹优化与控制
程志强 朱纪洪 袁夏明 王向阳
(1.清华大学计算机科学与技术系,北京 100084;2.复杂舰船系统仿真重点实验室,北京 100161)
1 引言
近年来,无人机控制与编队飞行[1-2]受到了广泛关注.其中具有垂直短距起飞能力的固定翼飞机是无人机控制中的研究热点.这种飞机既具有固定翼飞机高效的气动效率,又具有传统旋翼飞机灵活的起降能力,在军事和民用上具有很大的应用价值.垂直短距飞机具有低速悬停、高速巡航和过渡过程3种飞行状态,其中低速悬停阶段和高速巡航阶段均可以使用线性控制器进行控制,而过渡过程控制则面临强耦合、强非线性的控制难题[3].常见的垂直短距飞机有3种,分别是倾转旋翼飞机、尾座式飞机和推力矢量垂直短距飞机.其中推力矢量垂直短距飞机可用作战斗机,如F--35B.该类型飞机是由三轴承推力矢量喷管和升力风扇以及滚转喷管组成.
当前,对于垂直短距飞机过渡过程的研究主要集中在倾转旋翼和垂直短距飞机上.尾座式飞机除了面临起降上的问题[4-6]外,在进行过渡过程转换时也面临较强的非线性.在文献[7]中,一种基于增益预制的过渡过程轨迹控制方法被应用于尾座式无人机控制,其过渡过程轨迹是由预训练的人工神经网络生成的.虽然该方法仿真结果较好,但由于真实的状态分布很可能与训练中的状态分布不同,神经网络生成轨迹的质量仍有待进一步论证.在文献[8]中,通过限制尾座式无人机高度的变化并优化水平加速度,离线生成了过渡过程参考轨迹.而文献[9]针对尾座式飞机,使用最速下降法优化出一条过渡过程轨迹,却没有讨论在实际控制器中如何使用该轨迹.尾座式飞机最常用的控制方法是寻找一条关于俯仰角的过渡过程轨迹,原因是尾座式飞机过渡过程中的非线性主要是俯仰角变化引起的,这与倾转旋翼以及推力矢量垂直短距飞机均有很大的不同.在文献[10]中设计了一种针对倾转旋翼飞机过渡过程的速度控制器,而统一速度控制器[11]是该控制器的改进版.统一速度控制器的优点在于可以同时控制悬停、巡航和过渡过程,而不必在不同的控制器之间切换.但该型控制器的缺点是过渡过程轨迹是由一阶滤波器生成.另一种鲁棒控制方法在文献[12]中提出,其通过设计目标函数,评估并选取不同的配平点形成轨迹,然后针对轨迹上的每一点设计鲁棒控制律.在执行过渡过程时,根据当前状态选择相应配平点的鲁棒控制律进行控制,从而完成过渡过程.而在文献[13-15]中提出了多种基于增广系统的鲁棒控制器,但他们均没有考虑过渡过程轨迹的设计问题.倾转旋翼飞机过渡过程一般的设计思路是根据不同的机翼倾转角和飞行速度预制增益,原因是该型飞机过渡过程的非线性主要是由于机翼倾转角以及动压变化引起的.
虽然推力矢量垂直短距飞机与倾转旋翼以及尾座式飞机有很多共性,但该飞机仍然有自身特性需要在设计过渡过程控制器的时候进行考虑.首先最为明显的一点是由于推力矢量垂直短距飞机布局的差异,引起过渡过程中非线性的变量主要有3项:三轴承推力矢量喷管转角,升力风扇转角以及飞行速度.如果直接套用倾转旋翼增益预置与生成轨线的方法将会极大的增加内存使用的数量和设计的难度.如果固定升力风扇转角,部分倾转旋翼的过渡过程方法将可以使用,但这必定会损坏控制效果.在文献[16]中,过渡过程控制器就建立在固定的升力风扇转角的基础上.其次,对于其倾转旋翼来讲,由于机翼本身转动惯量较大,机翼倾转角的带宽要远低于其它执行器的带宽.故对于倾转旋翼飞机来讲,机翼倾转角并不参与姿态控制.但对于推力矢量垂直短距飞机来讲,三轴承推力矢量喷管和升力风扇转角带宽要比涡喷发动机高,故在过渡过程控制中仅使用推力和舵面控制姿态将会取得较差的控制效果.反之,如果使用3BSD喷管转角和升力风扇进行控制将会面临非线性控制的难题.
目前关于推力矢量垂直短距飞机过渡过程控制的文献较少,大部分是洛克希德公司发布的关于F--35B飞机的控制方法.F-35B的控制特点在于可以通过分配主发动机的推力来直接进行俯仰控制[17],但其机械传动结构过于复杂.本文使用了一个电动涵道来作为升力风扇的动力,在控制结构上与F--35B有较大的不同.针对推力矢量垂直短距飞机涡喷发动机低动态的特点,在全面考虑执行器动态和饱和的基础上,本文使用梯度下降法优化得到最优过渡过程轨迹.优化所得轨迹非配平点组成的,这一点与文献[12]有很大不同,也使得传统针对配平点设计控制器的方法失效.针对过渡过程轨迹上的点是非配平点的问题,设计了一种特殊的前馈加反馈控制器.为了验证新方法的鲁棒性和有效性,本文对气动参数等进行了参数摄动,并进行了仿真验证.作为对比,本文亦实现了文献[12]中过渡过程算法,仿真结果说明了本文提出的算法具有良好的动态特性和鲁棒性.
2 推力矢量垂直短距飞机气动建模与分析
由于推力矢量垂直短距飞机的滚转喷嘴可以很好地控制横行向状态并使之可以与纵向状态解耦,本节将会建立推力矢量垂直短距飞机的纵向状态方程并忽略横行向对飞机的影响.在本文中,对F--35B飞机进行了9:1的缩比研究.图1和图2展示了缩比F--35B战斗机的布局.
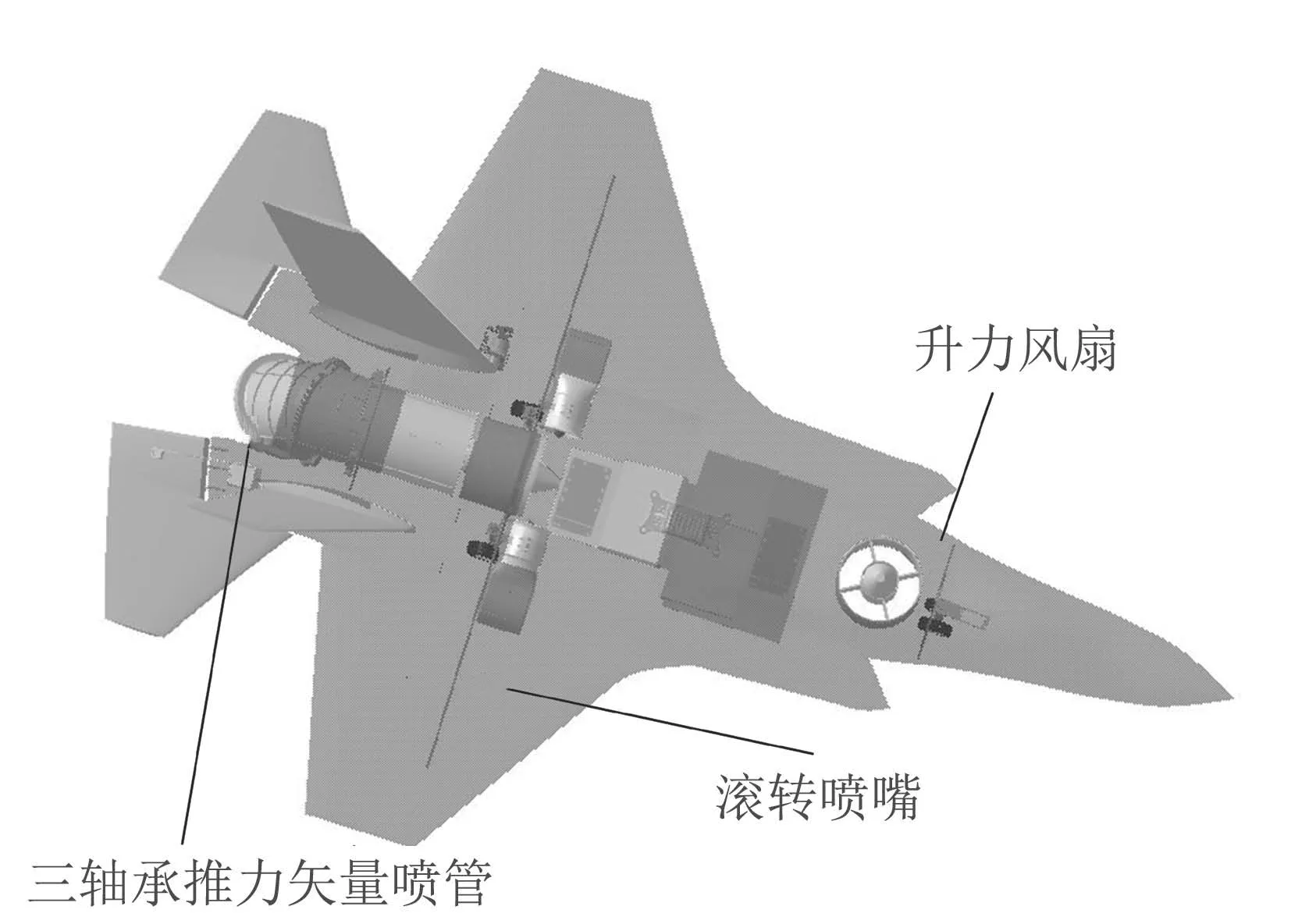
图1 F--35B缩比飞机模型俯视图Fig.1 Top view of F--35B reduced ratio aircraft model
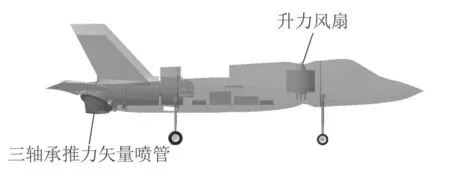
图2 F--35B缩比飞机模型侧图Fig.2 Side view of F--35B reduced ratio aircraft model
为了简化F--35B复杂的轴承驱动升力风扇动力系统[17],本文使用电动涵道作为升力风扇的动力装置.缩比模型还包括了一个推力矢量喷管和涡喷发动机.图3展示了推力矢量垂直短距飞机纵向推进系统,其主要参数列在表1中.
飞机纵向状态变量包括9个变量,依次是Vxg,Vzg,q,θ,δe,TF,δF,TN,δN.其中Vxg和Vzg是地面坐标系的x轴和z轴的速度.本文z轴的正方向指向地面.q 是俯仰角速度而θ代表飞机俯仰角. δe是升降舵偏角.TF和TN分别代表升力风扇推力和主发动机推力.δN是推力矢量喷管的纵向偏转角,δF是升力风扇的偏转角.

图3 推力矢量垂直短距飞机纵向推进系统Fig.3 Vectored forces of the propulsion system
飞机的纵向状态方程可以列写为式(1):

式中:γ是航迹角,ρ是空气密度,V 是真空速.CL,CD和Cm分别是飞机的升力系数、阻力系数和俯仰力矩系数.为了全面考虑执行器动态,本文使用us代表执行器的真实状态,即us=[δeTFδFTNδN]T.us,i代表向量us中第i个分量.uc代表执行器的输入指令,同样uc,i代表向量uc的第i个分量.本文将推力矢量垂直短距飞机执行器的动态用一阶惯性环节来建模,可得

其中:i是大于0小于4的整数,ri代表第i个执行器的速度极限,而pl,i和ph,i代表第i个执行器的位置极限.所有的执行器参数均在表2中列出.从表中可以看出,主发动机的带宽要远低于其他执行器的带宽,这客观上加大了垂直短距飞机过渡过程控制的难度.在过渡过程分析与设计的过程中忽略的执行器动态会导致控制效果恶化甚至会出现不稳定的情况.
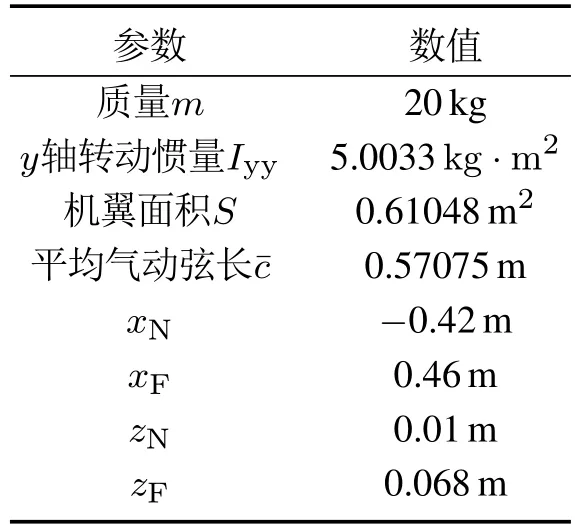
表1 缩比F--35B主要参数Table 1 General characteristics of reduced ration F--35B
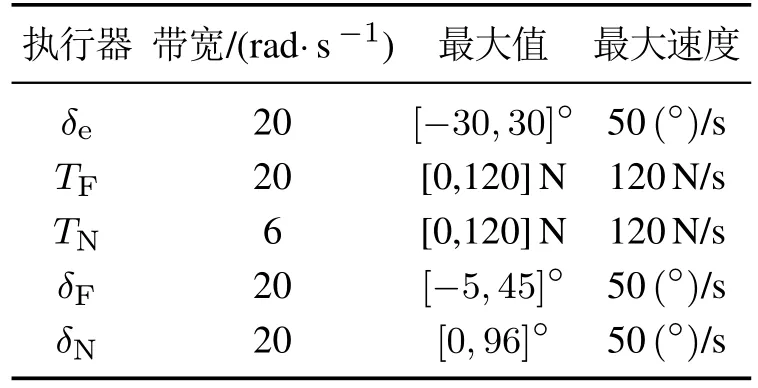
表2 执行器带宽及饱和参数Table 2 The bandwidth and limit of the actuator
为了将执行器动态包含到过渡过程控制器的分析与设计过程中,本文增广了系统的状态方程.增广后的状态可表示为x=[VxgVzgq θ δeTFδFTNδN]T.则总的状态方程可以表示为

其中:f(x)和B包含了飞机动力学和执行器动态,pl和ph是执行器的位置极限.
3 过渡过程最优轨迹设计
3.1 过渡过程代价函数
一般动态最优问题是寻找一个随时间变化的控制函数uc(t)使得如下的代价函数最小:
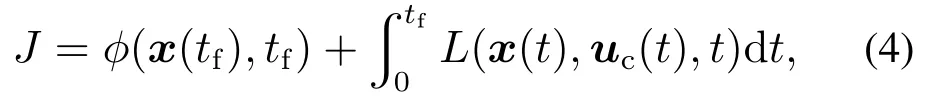
且该函数uc(t)应满足方程(3)的约束.在式(4)中,ϕ衡量了过渡过程终点与期望终点的距离,而L函数则衡量了在整个过渡过程中控制量和状态量是否满足实际要求. tf是整个过渡过程所用的时间.在本文,tf也是一个待训练的参数,具体方法将在下节展开.
为了统一考虑飞行状态和执行器动态及饱和,本文对系统状态和控制输入的不等式约束引入罚函数.对于一般的不等式约束:
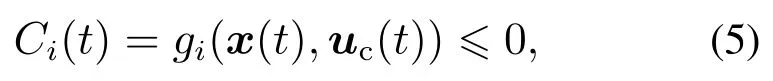
其中:gi表示第i个不等式约束,Ci表示gi的函数值.则罚函数具有如下形式:
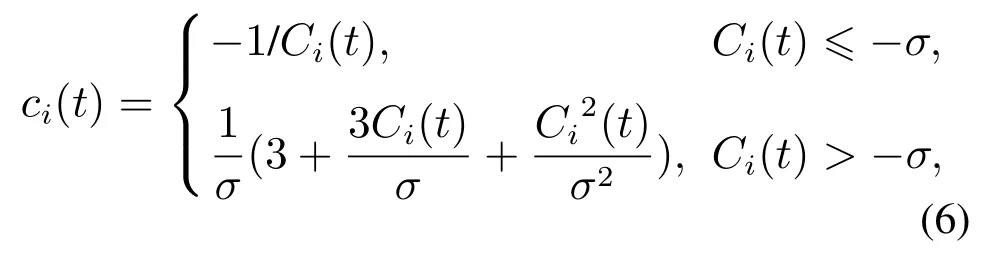
其中σ是罚函数参数,一般可设为1或者更小的数值.对于系统状态而言,本文期望所得最优轨迹中的状态均满足
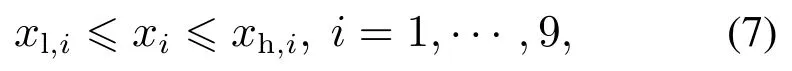
其中xl,i和xh,i是第i个状态的上下边界.飞机纵向的9个状态的边界值在表3中展示.为了防止飞机触底,Vzg应当为负数,且在过渡过程中保持较小的绝对值.
在明确边界的情况下,飞机状态的不等式约束gi具有以下表达形式:

其中i的变化范围为1到9.为了考虑执行器速度饱和的情况,uc(t)也应当建立合适的罚函数防止速率饱和.本文中给关于uc(t)的不等式为

相应gi函数形式为

其中j的变化范围为1到14.可见本文共引入14个罚函数来对状态和控制输入进行约束.
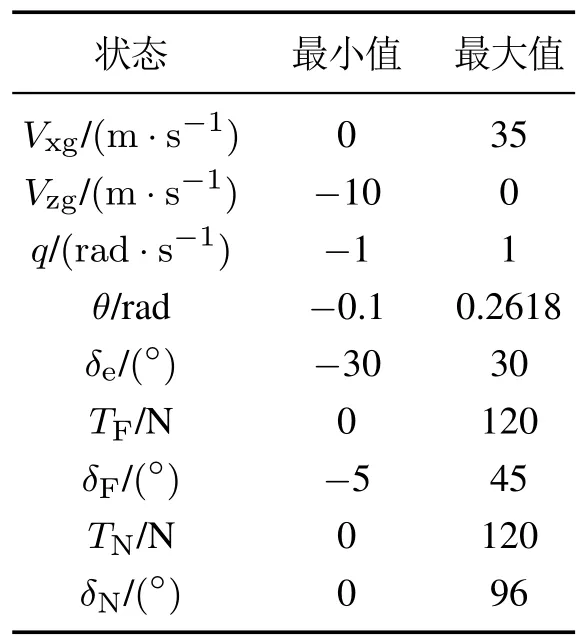
表3 状态变化范围Table 3 Bounds for states
在引入罚函数的基础上,系统的代价函数可以扩展为

进一步,衡量了过渡过程终点与期望终点的函数ϕ具有如下形式:

考虑起飞过渡过程(悬停到巡航)与着陆过渡过程(巡航到悬停)的不同,函数L(x(t),u(t),t)也应具有不同的过渡过程特性.对于起飞过渡过程来讲,为了确保飞机安全,飞机在整个过程中应该处于爬升状态.但考虑到由发动机与升力风扇提供推力的情况下,在过渡过程中向上爬升过多必然会浪费大量燃料.故向上爬升的约束只在状态罚函数ci(t)中体现,而在起飞过渡过程中最重要的是节省燃料.L函数具有以下表达形式:

而对于着陆过渡过程而言,过渡爬升将会导致悬停下降时消耗过多的燃料.故着陆过渡过程需要限制飞机的爬升,其L函数可表示为

以上便建立了轨迹优化中的优化目标.
3.2 最优化方法
由于系统状态方程中包含有大量的非线性项,故无法求出解析解.本文使用最速下降法来计算控制变量的数值解.为了优化过渡过程时间tf,本文采取文献[18]中的处理方法,将结束时间视为常数值1,则对于N个采样点来说,采样周期等价为T=1/N,相应的系统状态方程变为

其中h(x)=tf×f(x)且B∗=tf×B.则tf和向量组uc(t0),···,uc(tN−1)就是待优化参数.根据最速梯度下降法,哈密顿方程可被定义为

其中λ是拉格朗日乘子.通过龙格库塔积分方法,λ(i),i=0,···,tN−1可以根据解微分方程(16)和边界条件(17)来解得.

则uc(t0),···,uc(tN−1)的导数可以直接通过式(15)求导得到.则uc(ti)可通过如下公式进行更新:

其中l是学习率.
在实践中,按照该方法计算所得导数变化非常剧烈,直接应用会导致较慢的收敛速率甚至发散.因此本文采用了Adam(adaptive moment)[19]方法对导数进行优化.该方法在使用导数优化参数时,Adam方法采用如下步骤:

其 中:β1=0.9,β2=0.999,ε=10−8,Vdw和Sdw初始值都是0.除了应用Adam方法来提高算法的收敛效率,还对dw′进行了归一化处理,使得最终更新参数时,导数的最大数值不超过1.即
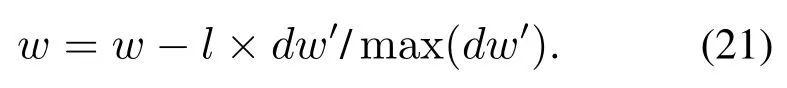
在使用Adam方法时,学习率一般在0.1到0.001间选取,本文中使用的学习率是0.01.通过以上方法,训练的稳定性得到了极大的提高,收敛速率也明显加快.
3.3 最优化结果
本文中的推力矢量垂直短距飞机在悬停时的配平状态和过渡过程结束时的目标状态如下:
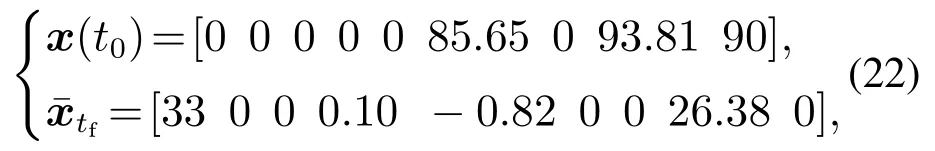
而在巡航状态下,配平状态和过渡过程目标状态如下:

事实上在实际操作过程中,飞机切换时的状态未必是严格的配平状态.这就要求过渡过程控制器要具有足够的鲁棒性.具体如何使用最优化轨迹设计控制器,将在下一节介绍.在明确了过渡过程初始状态和目标状态后,起飞过渡过程最终tf优化为7.4 s,而对于着陆过渡过程则优化为12.7 s.本文的采样点为500个,且所有积分采用四阶龙格库塔积分方法.在经过最优化后,起飞过渡过程的轨迹如图4和5中所示.而着陆过渡过程如图6和图7所示.
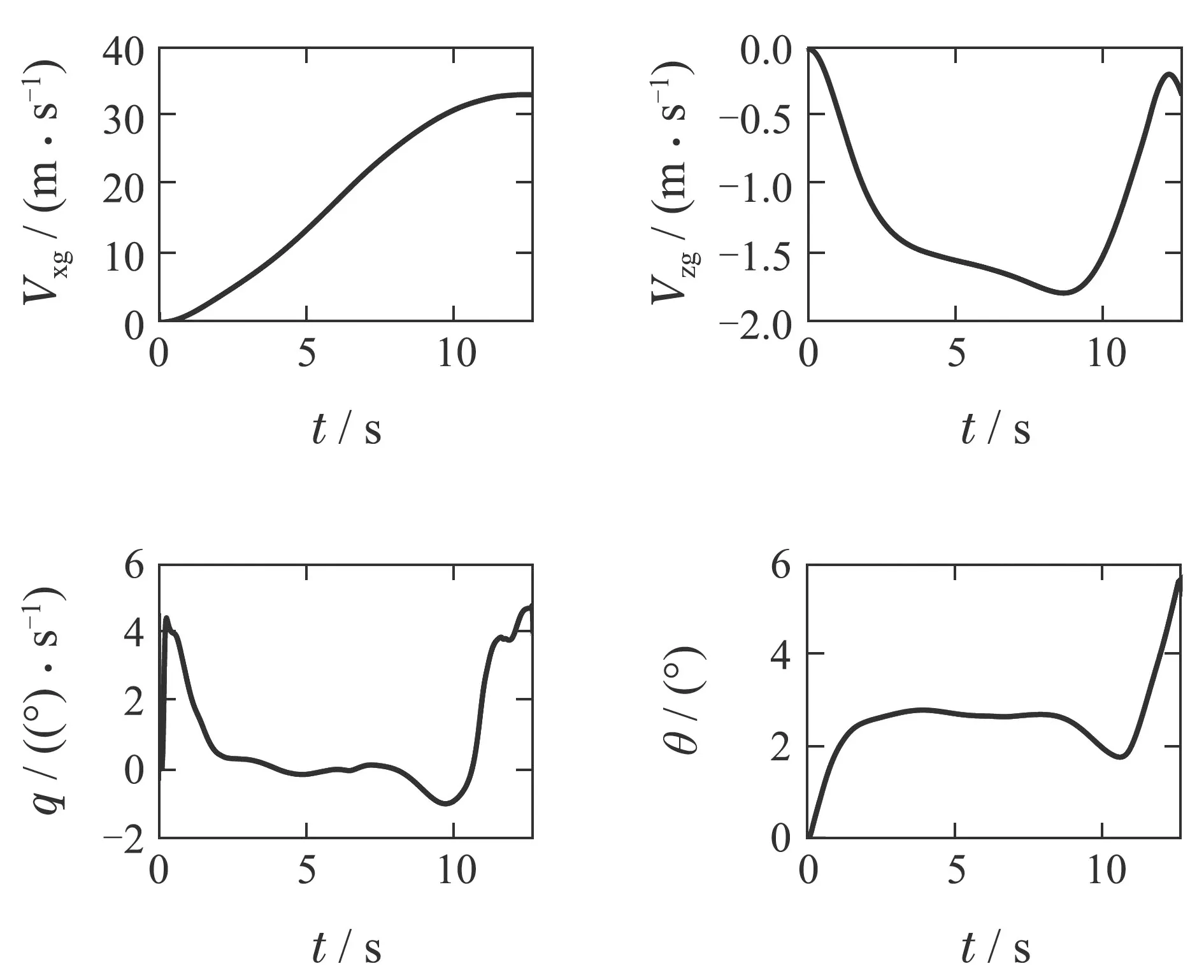
图4 起飞过渡过程最优轨迹中的飞行状态Fig.4 The optimal trajectory of takeoff states

图5 起飞过渡过程最优轨迹中的控制量Fig.5 The control value of takeoff optimal trajectory
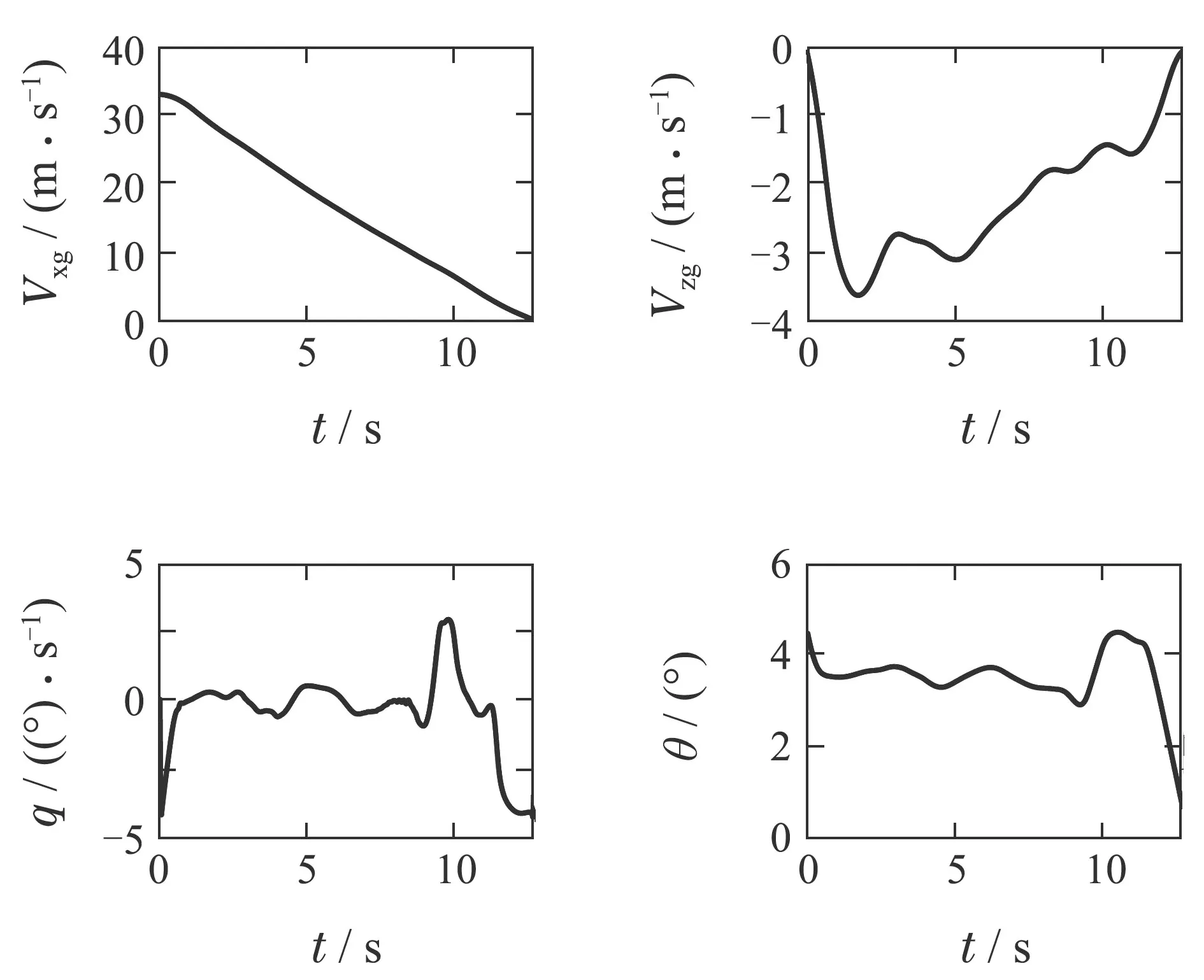
图6 着陆过渡过程最优轨迹中的飞行状态Fig.6 The optimal trajectory of landing states
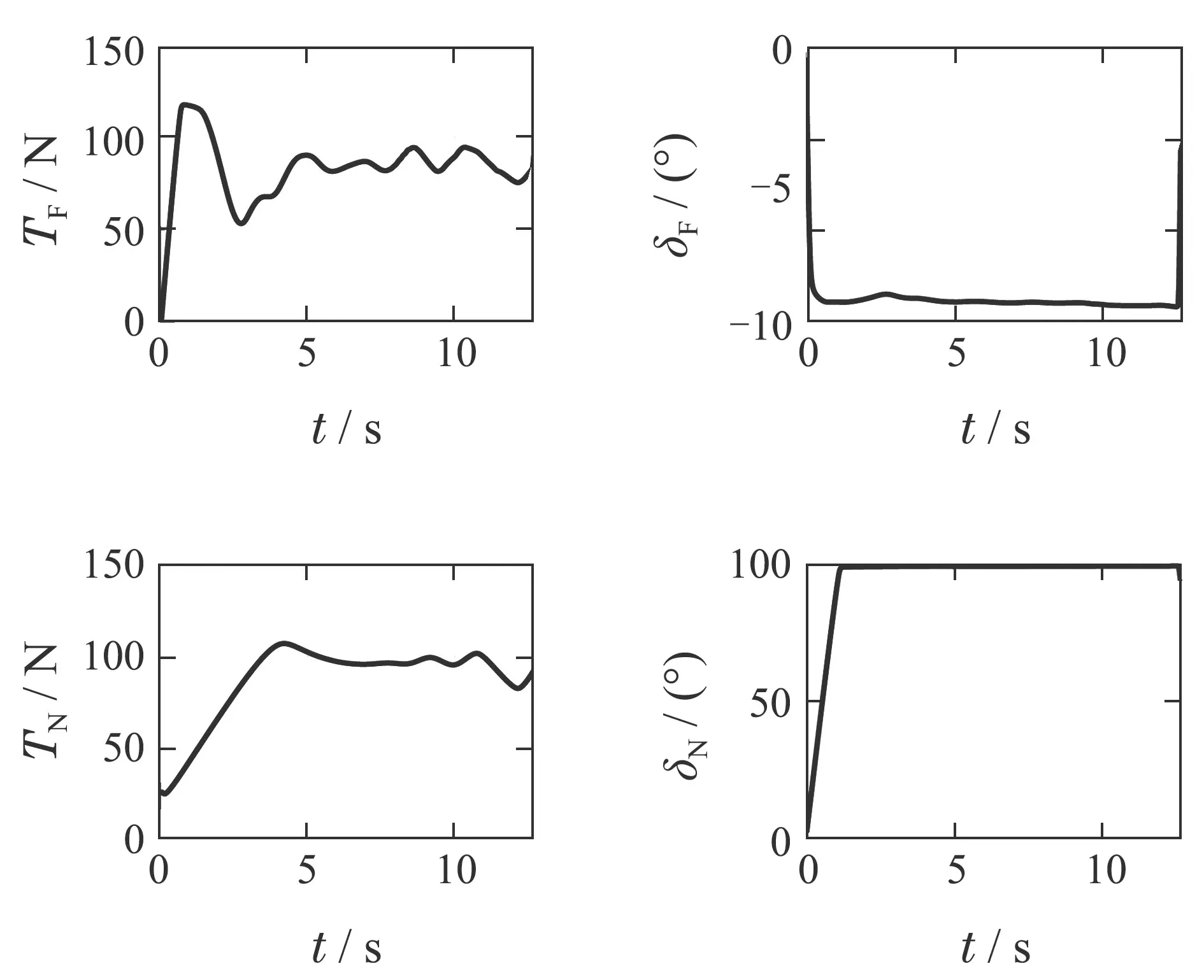
图7 着陆过渡过程最优轨迹中的控制量Fig.7 The control value of landing optimal trajectory
从图中可以看出,在进行起飞过渡过程时,升力风扇偏角δF较大,代表最优过渡过程曲线使用了升力风扇进行前向加速.而在进行着陆过渡过程时主要依靠较大的推力TF和TN进行减速.总体而言,最优化轨迹有过渡过程时间短俯仰角变化小的优点,可以在实际过渡过程中使用.
4 基于最优轨迹的过渡过程控制器设计
在计算得到最优轨线后,极少有公开的论文探讨如何使用最优轨线.显然过渡过程轨迹计算量大,难以在飞控计算机上实时计算得到.同时对于一条优化完毕的最优过渡过程轨迹而言,由于实际模型和标称模型之间一定存在差异,开环控制不能帮助飞机完成过渡过程.本文通过引入反馈控制,并将最优轨迹作为一种特殊的前馈控控制,提出了一种基于最优过渡过程轨迹的控制器.本文将最优过渡过程轨迹状态表示为(ti),控制量表示为ti).控制结构框图见图8.

图8 控制结构框图Fig.8 Control structure
在图8中:ub(t)表示反馈控制量,uf(t)表示前馈控制输入.最优化轨迹根据现在飞机状态找到轨迹中最相近的状态,并将返回下一状态的期望状态和预制的控制量值.则期望状态和真实状态之间的差值∆x(t)=(t)−x(t).由于最优过渡过程轨迹是由离散点组成的,离散点以外的状态和控制量应由插值得到.即对于时间ti≥t 由于建模误差、测量噪声、大气扰动等存在,真实飞行状态x(t)和期望的最优过渡过程轨迹状态(t)一定存在差异.因此应通过反馈控制的方法使得真实飞机状态x(t)能够追踪过渡过程轨迹并完成过渡过程.首先可以使用∆x(t)计算系统状态x(t)所需的额外加速度.本文将使用上角标d来表示期望的额外加速度. 其中MD分别是Fxg,Fzg,My对δe,TF,δF,TN,δN的导数.则问题转化为了一个控制分配问题,可以通过多种方法求解.本文使用最简单的计算矩阵MD的伪逆来计算ub(t),即 最后,通过尝试可以得到过渡过程控制器和平飞控制器以及悬停控制器之间的切换条件.考虑到升降舵效率随着真空速的变大而不断提高,切换条件应当由最低空速和足够小的TF组成.该条件可以用(27)来表示.如果飞机的飞行状态满足该条件,则飞机控制器应当切换为平飞控制器. 如果飞机从开始过渡过程到达到该条件所用的时间小于标称的过渡过程时间,意味着过渡过程轨迹并没有完成,推力矢量喷管转角离0◦还有一定距离,在这种情况下通过仿真分析可以得出结论,在满足该条件下的切换控制器并不会对飞行安全造成威胁.原因是在悬停以及过渡过程开始时,TN产生的低头力矩主要由TF产生的抬头力矩所抵消,而当TF足够小时,TN产生生的低头力矩已可以由升降舵抵消,当切换控制器后,δN会快速减小,随之其产生的低头力矩也会快速减小.由于此时升降舵控制效能已较大,且带宽与推力矢量转角相同,故由δN减小产生的低头力矩减小会快速的由升降舵补偿掉.此时飞机虽有轻微的抬头动作,但不会危及飞行安全. 相对的是着陆过渡过程切换条件: 该条件限定了在着陆过渡过程中,如果速度足够低,δN足够接近90◦,便可切换为悬停控制器. 本文平飞控制器和悬停控制器都由线性控制器进行控制.为了模拟噪声对控制器的影响,本文引入了ADIS16488传感器噪声作为加速度计和陀螺的标准噪声.为了验证控制器的鲁棒性,对飞机参数,S,m,xF,xN,Iyy,zN,zF加入了±10%的参数摄动.对于起飞过渡过程初始状态,Vxg误差为±2 m/s,而Vzg误差为±1 m/s,θ为±2◦.对于着陆过渡过程,Vxg误差为±5 m/s,其余摄动与起飞过渡过程相同.对摄动参数排列组合后进行仿真,均取得了较好的控制效果.为了对比,本文选择文献[12]中的过渡过程控制器作为对比控制器.该控制器的优点是在设计时可以很方便的考虑执行器动态,避免了因忽略动态而造成的控制失稳的情况.同时该控制器也是基于轨迹的控制器,方便与本文的控制器进行对比.仿真结果如图9-12所示. 图9 起飞过渡过程飞行状态对比曲线Fig.9 The response of takeoff states 图10 起飞过渡过程控制量对比曲线Fig.10 The response of takeoff control values 图11 着陆过渡过程飞行状态对比曲线Fig.11 The response of landing states 图12 着陆过渡过程控制量对比曲线Fig.12 The response of landing control values 在图9中可以看出,本文提出的控制器可以在8 s左右的时间完成起飞过渡过程,相比较而言文献[12]中的控制器用了20 s才完成过渡过程,而其空速依然较慢.在着陆过渡过程控制中,本文提出的控制器依然具有时间短,过渡过程平稳的特性.为了进一步对比两种方法的控制精度,本文计算了两种方法在过渡过程阶段的状态跟踪误差的2-范数,如图13所示.从中可以看出,所提出的的方法具有较好的控制精度. 图13 过渡过程阶段跟踪误差范数随时间变化图Fig.13 The norm of tracking error in transition 本文提出了一种针对推力矢量垂直短距飞机过渡过程的控制方法.该方法通过系统的考虑执行器动态和饱和条件,使用Adam方法加速优化,最终给出了不同过渡过程时间下的最优轨迹.在控制器设计时,将该轨迹的控制量作为控制前馈,根据实际状态和参考轨迹状态给出反馈量,实时修正当前状态,使之按照预设轨迹进行过渡.新方法具有在线计算量小和物理意义明确的优点.通过与文献[12]仿真结果对比,进一步验证了本文方法具有更好的动态特性和平稳性.同时,通过大量的参数摄动仿真,验证了该方法具有较强的鲁棒性.

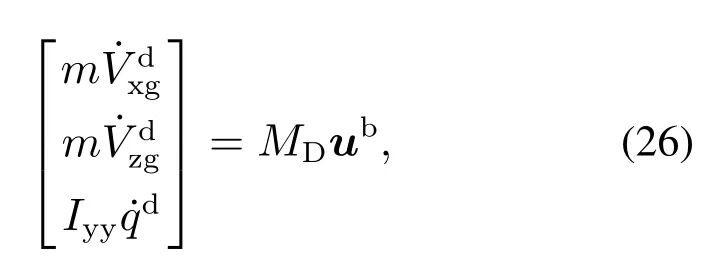









5 总结

