飞行机械臂系统的接触力控制

孟祥冬 何玉庆张宏达杨丽英谷 丰韩建达

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室,辽宁沈阳 110016;2.中国科学院机器人与智能制造创新研究院,辽宁沈阳 110016;3.中国科学院大学,北京 100049;4.广州中国科学院沈阳自动化研究所分所,广东广州 511458)

1 引言

旋翼无人机(rotor unmanned aerial vehicle,RUAV),又称旋翼飞行机器人,在过去几十年间得到了快速发展,使得这类飞行器已经具备垂直起降、定点悬停和超低空飞行等一系列优点,并且广泛应用于军事和民用领域,例如反恐防暴[1]、情报侦查[2]、灾难救援[3]和精准农业[4]等.然而,现有关于旋翼无人机的应用通常是将其当作一个搭载传感器的感知和运动平台,在飞行过程中不会与外部环境发生任何接触.

在最近几年,由旋翼无人机和机器人操作臂构成的飞行机械臂系统(aerial manipulator system),已经逐渐成为机器人领域中一个新的研究热点.相比于传统的飞行机器人,飞行机械臂系统可以与外部环境发生交互作用,并能进行一些主动作业任务.现有研究大都集中在目标物体的抓取、码放和运送方面.文献[5]使用一个五自由度飞行机械臂系统实现了对圆柱形物体的抓取.文献[6]设计出一个仿人的双臂飞行机械臂来进行抓取操作.文献[7]研究使用两个六旋翼飞行机械臂系统协作搬运一个轻质长杆.文献[8]在六旋翼飞行平台上安装七自由度操作臂来对运动目标进行抓取.文献[9]则设计出一个集成了飞行机械臂和地面移动平台的运输协作系统,来合作运送重物.以上这些研究的飞行机械臂交互操作都是在无人机平台处于自由飞行条件下进行.尽管交互过程中会产生接触力,但是通常忽略接触力的存在,不考虑所产生的影响.

最新的研究工作开始对飞行机械臂在接触作业过程中产生接触力及其控制的问题展开了探索.文献[10]为小型四旋翼无人机设计了一个复杂的两自由度机械臂,用于将接触环境时所产生的动能转化成弹性机构的势能,以保证接触环境过程中无人机平台的稳定飞行.文献[11]使用了线性二次型调节器优化状态反馈的控制方法来控制一个持续作用在墙面上的接触力,并且所提出的方法在四旋翼平台上得到验证.文献[12]设计了一个八旋翼飞行机械臂系统携带探伤设备用于桥梁损伤检测的任务,并将测量力反馈加入到无人机位置控制环路中来实现接触操作中接触力控制.文献[13]设计了一个六旋翼单自由度飞行机械臂系统进行按压急停开关关闭电灯的操作.以上研究及实验结果表明,现阶段飞行机械臂系统在与环境交互时的接触力控制依旧面临许多亟待解决的问题.其中飞行机械臂的恒定接触力控制就是一个具有挑战性的问题,这同时也是本文重点研究的内容.

一般来讲,机器人的接触力控制需要将力传感器信号作为反馈来设计力控制环路[14].而力信号通常又是通过传感器应变元件的受力形变来获得.然而,无人机在飞行时,由于高速旋转螺旋桨的气动作用，机体存在一定的振动[15].因此,机载使用力传感器测量环境接触力,就会出现较大噪声,导致测量误差变大,最终降低飞行机械臂系统的接触力控制精度.为避免直接使用力传感器所带来的缺点,本文依靠无人机接触环境时的力平衡关系来间接获得接触力信息.

本文的研究工作旨在提出一种有效的接触力控制方法,用于保证飞行机械臂接触外部环境时能够可靠地进行作业.因此,本文研究了在外部力作用下的无人机位置响应,并从理论上首次证明闭环无人机系统具有与弹簧-质量-阻尼系统相同的动力学特性[16].同时,基于阻抗控制的思想[17],创新地提出了飞行机械臂系统的接触力控制方法.由于旋翼无人机系统加装了机器人操作臂,导致这类新型飞行器动力学与常规系统模型存在一定的差异:一是本体动力学模型更加复杂,二是整体模型建模困难.同时存在的接触力对无人机位置和姿态角控制也带来两方面区别:一是接触模态下的本体安全、动态稳定控制更加重要;二是需要解决接触模态下力和位置混合控制的问题.

本文的其他部分内容安排如下:第2部分研究了无人机系统的位置响应与外部施加作用力之间的关系,并且从理论上证明了闭环无人机系统具有与质量-弹簧-阻尼系统一致的动态特性.第3部分基于阻抗控制思想,提出了飞行机械臂系统的接触力控制方法,并进行了稳定性分析.第4部分介绍了所开发的新型飞行机械臂系统,并通过实际的飞行实验证明所提出方法的有效性.最后一部分对本文所做的研究工作进行了总结.

2 闭环无人机系统的模型推导

本部分首先对常规的旋翼无人机系统设计一般的姿态和位置控制器.然后基于控制器结构,对闭环无人机系统进行再建模,研究无人机位置响应与所受到外部作用力之间的关系.最后证明位置闭环无人机系统具有类似于弹簧-质量-阻尼系统的动态特性.

2.1 常规无人机系统动力学模型

多旋翼无人机是一种由多个旋翼对称分布而构成的飞行器系统.为不失一般性,本文选择普通四旋翼无人机建立动力学模型,坐标系的定义如图1所示.

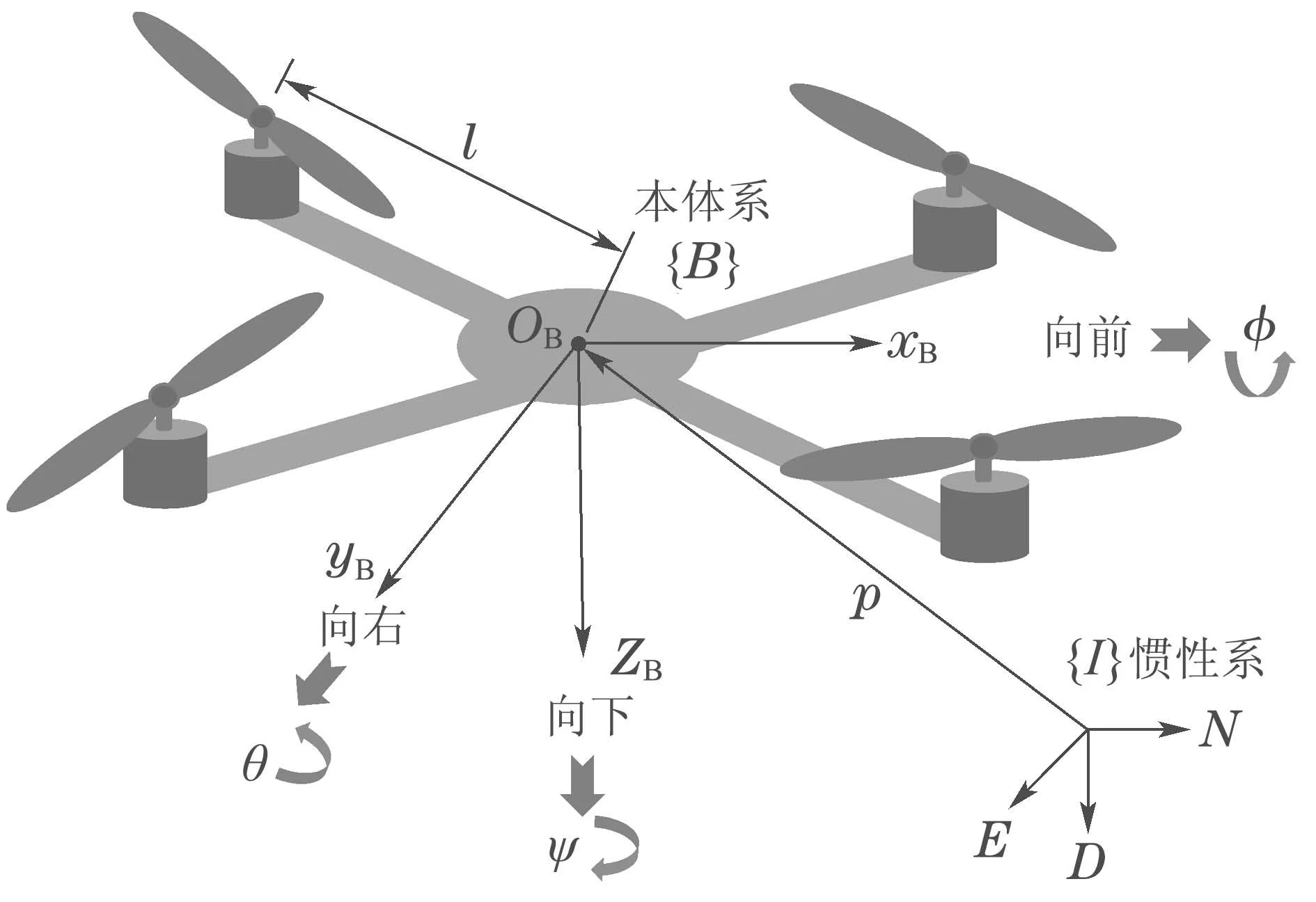
图1 旋翼无人机系统的坐标系定义Fig.1 Coordinate system definition for RUAV system

图中:惯性坐标系{I}采用北东地(north-eastdown,NED)坐标系;本体固定坐标系{B}的原点位于无人机系统几何中心并与质心重合,坐标轴xB,yB,zB方向对应选取前右下指向;{B}在{I}系中的位置向量为P=[x y z]T∈R3;欧拉角Φ=[ϕ θ ψ]T∈R3分别对应表示滚转、俯仰和偏航姿态角,本文核心内容是研究飞行机械臂的接触力控制问题,而不要求无人机做大姿态角度的机动飞行，因此实际姿态角范围始终能够满足条件−

可以得到无人机系统在惯性系下的平移动力学和姿态动力学模型[18],即为

其中:系统质量m∈R;g是重力加速度9.81 ms−2;转动惯量I=diag{Ix,Iy,Iz}∈R3×3;l是从机体中心到电机轴的距离;ai和bi都是常数,定义为a2=;u1是无人机系统升力,u2,u3和u4分别对应到各轴上的旋转力矩.

2.2 无人机系统常见控制器结构

无人机控制器通常使用内-外环结构,即姿态子系统作为内环,位置子系统作为外环.在本节内容中,首先为无人机设计姿态和高度控制器来实现平稳的空中飞行,进而设计位置控制器来实现无人机在三维空间定点悬停.整个系统对应的控制框架如图2所示.

图2 无人机系统控制框图Fig.2 Control block diagram of UAV system

2.2.1 姿态控制器

首先对无人机的姿态动力学式(1b)使用反馈线性化方法转化成一个线性系统,此时,系统的虚拟控制量与原来控制量u2,u3,u4的关系为

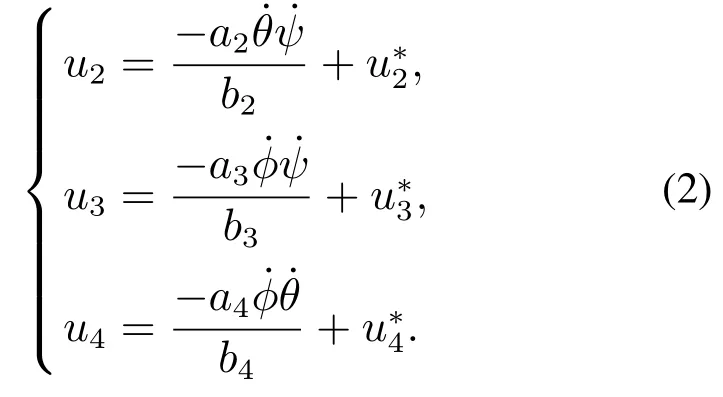
针对所得到的系统,设计如下状态反馈控制器:

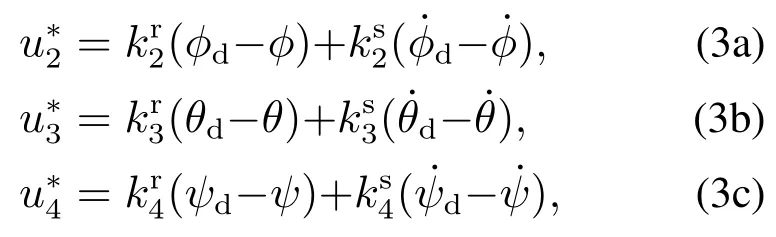
2.2.2 高度控制器

无人机的三维位置控制通常分成高度控制和水平位置控制.对于式(1a)中的高度动力学,使用变量代换

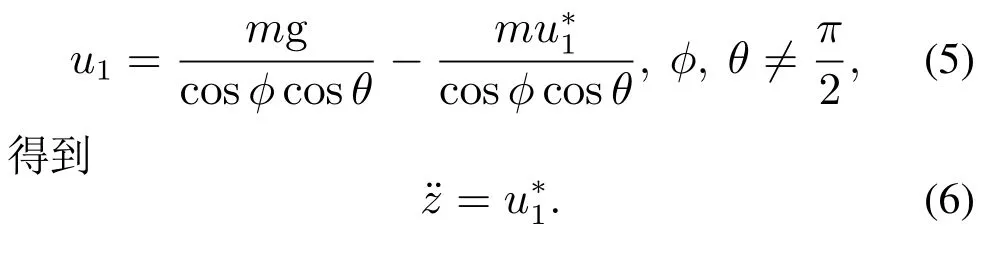
对所得到的模型,设计如下状态反馈控制器:

2.2.3 水平位置控制器

基于常用的内-外环控制,内环姿态角度的期望值是由外环位置控制的输出计算得到,由式(1a)可得

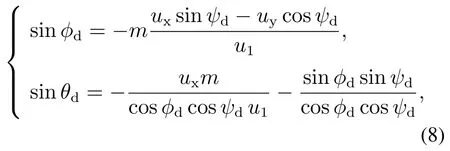
其中:ux和uy是水平位置控制器的输出;是位置控制器的增益系数,即

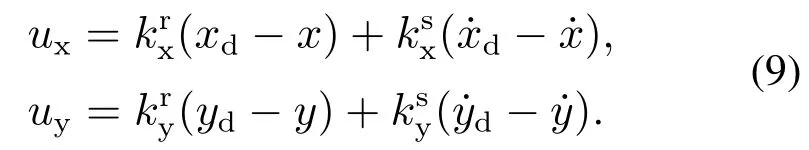
无人机在控制器作用下可以实现三维空间中稳定悬停,此飞行状态下的姿态角度变化较小.因此,将式(9)代入到式(8)中,再经整理可以得到

2.3 闭环无人机系统的再建模

其中zd选取坐标原点作为期望悬停高度,由此可得无人机高度在外力作用下的动态响应关系为

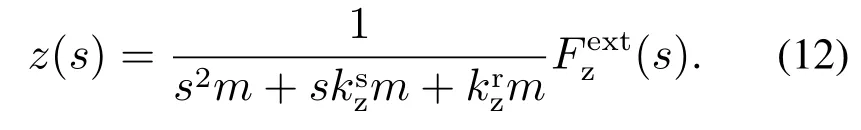
当研究无人机水平位置受力特性时,可以将航向角度设为0,从而有sin ψ=0, cos ψ=1.同时也选取坐标系原点作为期望的悬停位置.那么,式(1a)对应的系统水平运动动力学可以写为

对式(14)进行拉普拉斯变换,将式(4)和式(10)代入后,可以得到无人机系统水平位置x和y对应在外部力作用下的动态响应关系为式(15):

继而再对式(15)分式中的分子分母分别除以各自的分子.注意到此时无人机已经处于位置闭环控制状态,当以此为平台的飞行机械臂系统接触外部环境时,所产生接触力或的变化频率相比较于无人机系统控制频率来讲比较缓慢.外部力作用在闭环系统上,其位置响应的频率较低.同时,无人机物理结构由轻质材料构成并且所有部件设计紧凑靠近几何中心,所以这类小型无人机实际转动惯量Ix和Iy的数值一般在10−2∼10−3kg·m2这个量级[18],是比较小的数值,使得因此,可以很合理地得到近似关系进而将式(15)可以写成

由式(12)和式(16)可知,闭环无人机系统在外部力作用下的位置响应(包括竖直高度和水平位置),类似于普通弹簧-质量-阻尼系统的动力学特性,如图3所示.

图3 闭环无人机等效为弹簧-质量-阻尼系统Fig.3 Closed-loop UAV system behaves as a spring-mass-damper system

2.4 水平接触力关系分析

当飞行机械臂系统在前向接触外部环境并施加某一水平接触力Fc时,根据作用力与反作用力的原理,环境也会给飞行机械臂系统施加反作用力−Fc.假设旋翼无人机在接触环境时依旧保持悬停飞行,并且保证接触力能够始终垂直于环境接触面.根据式(1a),可以得到在稳定接触状态下的平衡关系为

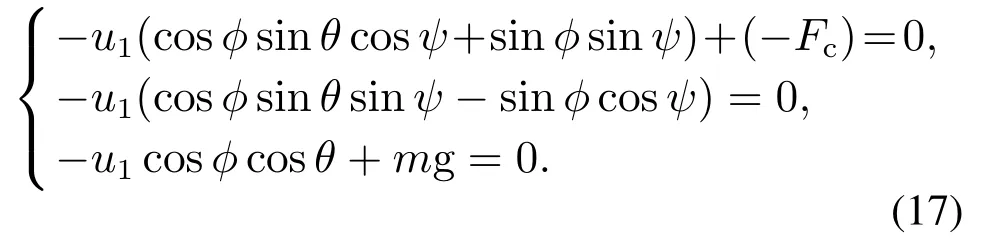
将航向设为固定值,即令ψ=0.因此可以根据式(17),推导出接触力Fc的表达为

可见,接触力Fc可以由飞行机械臂系统的重力mg和俯仰角度θ来共同确定,如图4所示.此时的无人机系统就相当于是一个可测量接触力的传感器.

图4 飞行机械臂系统接触力关系图Fig.4 Force relationships for aerial manipulator system

由图4可知,当接触力Fc出现时,无人机总会有一个俯仰角度θ与其时刻对应.若此时的接触力为期望控制力Fd,那么所对应俯仰角就是系统期望达到的俯仰角度θd.进而可以控制无人机跟踪这个期望的俯仰角θd来实现对Fd的控制.因此可由式(18)得到θd的值为

3 飞行机械臂接触力控制

本部分主要研究飞行机械臂的接触力控制.首先,简单的介绍阻抗控制原理;然后根据阻抗控制思想提出飞行机械臂系统的接触力控制方法.之后分析系统的稳定性问题.

3.1 阻抗控制原理

阻抗控制是由Hogan提出,用于解决机器人接触环境时的力控制问题[17],是通过调节位置和力之间的期望阻抗关系来实现机器人与环境之间的作用力控制.基于位置的阻抗控制原理是将环境刚度和机器人位置共同确定的轨迹输入到系统进行跟踪,从而间接实现力控制[19].这里提到的“间接”就是阻抗控制的核心思想,即通过控制机器人跟踪期望位置轨迹来实现最终的力控制.

3.2 飞行机械臂接触力控制

飞行机械臂系统在接触环境进行作业任务时,面临两个控制问题:一是要保证无人机平台的稳定飞行,二是接触过程中要控制接触力.现有关于无人机稳定性的研究工作已经实现第1个目标.对于第2个控制问题,本部分将使用第3.1节中提到的间接实现力控制思想加以解决,即根据力偏差计算出飞行器期望的位置轨迹并输入系统中来实现接触力控制.

由闭环无人机系统的特性可知,若期望位置和实际位置之间存在误差,系统就会产生相应的驱动力矢量µ=[µxµyµz]T∈R3.同时还会产生与之对应的期望姿态角(滚转角ϕd和俯仰角θd),以最终产生实现平移运动的分力[20].通常情况下,油门升力u1、驱动力矢量µ以及期望姿态角度ϕd和θd的关系如下:

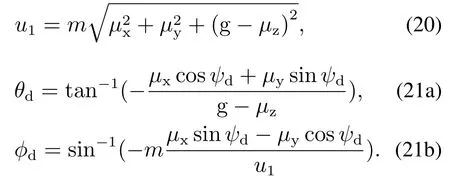
因此,如果根据期望控制的接触力,将计算所得的期望位置和对应期望姿态角度输入到无人机系统中,那么最终会产生期望的旋翼控制量.于是无人机将会在所接触环境上施加一定的作用力.上述就是阻抗控制的“间接”思想在飞行机械臂接触力控制问题上的应用,整体控制实现框图如图5所示.定义无人机的位置误差为∆x,系统期望位置的设定值为xd,由环境位置确定的飞行机械臂参考位置为xr,并有以下关系:

并且由已推导出的弹簧-质量-阻尼系统模型(16a)可以得到系统位置误差∆x和接触作用力Fe之间的关系为

其中定义Fe=Fd−Fc,并且Fc由式(18)得到,进而有xd=xr+∆x.此外,本文所提出的接触力控制方法旨在控制水平接触力,不论实际所接触环境表面特性具体怎样,只要在接触过程中保证牢固静态不滑动接触即可.因此,需要控制飞行机械臂末端姿态来补偿无人机俯仰角度θ,以保证是正交的接触力.

图5 飞行机械臂系统的接触力控制Fig.5 Contact force control of aerial manipulator system

3.3 动力学模型

接触状态下飞行机械臂系统动力学模型含有3个部分:无人机位置、无人机姿态和机械臂模型.这里以图4中所示单自由度旋转关节机械臂为例,机械臂基座安装在整体系统质心位置且保持正交接触,即为

根据上述公式可知,无人机的位置动力学式(24a)要受到环境接触力−Fc∈R3的影响,其中Fc为

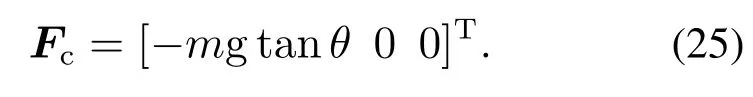
由于机械臂是垂直于接触面并且安装在系统质心位置，所以无人机的姿态动力学式(24b)仅会受到机械臂关节电机反扭矩τm∈R3的影响.其中:τm=[0 τm0]T是关节电机驱动扭矩τm的矢量形式,W=diag{l,l, 1}∈R3×3是系数矩阵,τ=[u2u3u4]T∈R3,e3=[0 0 1]T∈R3,转换矩阵RΦ(ϕ,θ,0)∈R3×3具体形式为

其余变量符号的定义同第2.1节中所示.

假设接触面不是绝对光滑且能够提供足够的摩擦力,对应的连杆重力全部由悬停的无人机平台和所接触的环境来分担.因此,常规的机械臂动力学模型此时就退化为关节电机模型式(24c).其中:θmrad是机械臂的关节角度,H kg·m2是关于电机轴的转动惯量,τr=u3N·m是无人机姿态控制过程中对机械臂旋转关节的反作用力矩.

3.4 稳定性分析

由上述分析可知,接触操作状态下飞行机械臂系统的稳定性与环境的刚度没有关系.只要保证各个系统的稳定性,那么整个系统稳定性就可以随之确定.因此,本节首先为3个子系统设计控制器,并分析稳定性.

3.4.1 控制器设计与稳定性

针对第3.3节中式(24)对应的各个系统分别设计控制器.机械臂的控制器用于控制关节角度和速度来跟踪期望的轨迹,同时要考虑无人机姿态动力学的耦合影响.无人机位置控制器的设计在保证位置稳定的同时,要补偿环境接触力作用.无人机姿态控制器的设计要在稳定姿态跟踪的同时,还要补偿机械臂关节控制反扭矩的影响.

本文研究的核心问题是接触作业型飞行机械臂系统的接触力控制方法与实现,旨在提出一个新的框架来解决飞行机械臂接触力控制问题.同时还希望那些已在飞行器上验证可用的控制算法经修正依旧能够满足新问题的需求,以便达到易于系统实现的目的.因此,首先对飞行器动力学进行反馈线性化,然后设计滑模控制器来分析系统稳定性[21].

针对式(24a)子系统定义新的输入量µ1,其具体形式如下:

对应的位置动力学式(24a)可以写成

对于式(24b)依旧采取式(2)中所述的反馈线性化方法,并令对角矩阵Wτ=I−1W∈R3×3.为了统一形式,定义新的控制量

所以姿态动力学式(24b)可以写成

因此,飞行机械臂各子系统对应模型都可以写成统一的形式

针对系统(32)设计滑模控制器,定义状态误差eξ为eξ=(ξd−ξ),滑模面定义为

其中矩阵C为系数对角正定阵.依据滑模理论,可以得到系统控制率为

其中:λ和γ是正系数;γ是有界扰动的上边界;sat(·)是具有边界层厚度δ的饱和函数,常用于削弱模型滑动过程中的抖振问题,其定义为

根据Lyapunov稳定性理论可知,系统(32)是渐近稳定的,系统状态ξ能够渐近收敛到期望值ξd.因此,当飞行机械臂系统进行空中接触操作任务时,只要对应各个子系统能够保证稳定性,那么整个系统的稳定性也就可以确定.

4 飞行机械臂系统与飞行接触实验

4.1 飞行机械臂系统介绍

如图6所示的飞行机械臂系统,机体采用轻质材料并且机械结构设计紧凑.飞行平台是一个普通的四旋翼无人机，所使用的飞行控制器是一款开源飞控[22].机械臂连杆由系统中心位置向前伸出,关节驱动采用一个大扭矩舵机.为了测量操作时的接触力信息,使用了一个单轴力传感器,并将其安装在机械臂连杆末端.力传感器可以通过数据采集板与飞控通信,测量力的信息可以由飞控实时记录.连杆末端安装了一个小型接触板用于保证接触的稳固性.关于系统的一些重要的物理结构参数,如表1所示.

图6 飞行机械臂系统Fig.6 Aerial manipulator system introduction

表1 飞行机械臂系统参数表Table 1 Parameters of aerial manipulator system

此外,为实现本文所提出的接触力控制方法,单自由度飞行机械臂的关节舵机需要实现自动控制,来补偿接触操作飞行平台的姿态角,以保证机械臂连杆正交于接触面.

4.2 飞行接触实验

本部分使用第4.1节所介绍的飞行机械臂系统,进行接触环境的力控制实验.首先介绍实验的环境和条件,然后进行斜坡力跟踪和恒定力控制实验来验证所提出接触力控制方法的有效性.

在室内环境下,使用NaturalPoint Optitrack动作捕捉系统来提供飞行器的位置和速度信息[23].而无人机的姿态运动信息则由机载惯性测量单元IMU来获得.自由飞行状态下旋翼无人机的位置控制精度为±0.03 m,其姿态控制精度为±0.03 rad.在下面的实验中,将无人机的航向设定为0,并且所接触环境的位置是[0.45 m,−0.92 m,−1.48 m].

本文的控制方法不需要接触力信号的直接测量,而是采用姿态反馈的方法间接实现.尽管是这样,笔者在实验过程中依旧加载了力传感器,其主要目的是获取真实的接触力信息,并与实际控制结果进行对比,以验证笔者方法的准确性,如图6中展示的物理系统所示.正如文章引言部分提到,飞行状态下机体的振动不可避免,并且是高频振动,会引起测量噪声.在使用力传感器测量时,一方面从数据层面进行低通滤波来减小高频噪声,另一方面是从结构层面解决,在连杆末端接触板上加装能够减小接触振动的软质垫层来进行缓冲.

飞行机械臂接触外部环境进行操作任务,其过程主要分为4个步骤:接近目标、接触过渡、接触力控制和返回,即如图7所示.本实验重点研究飞行机械臂接触环境时的力控制效果.

图7 飞行机械臂接触操作的主要步骤Fig.7 Main steps of aerial contact operation

将一个斜率为0.5 N/s终值为5 N的斜坡函数F(t)=0.5 N/s·t(0 ≥t ≥10)输入系统作为期望控制的接触力.当飞行机械臂系统接触环境时,就会在控制器的作用下跟踪这个期望力.若期望力数值不再改变时,还可实现恒定接触力的保持.相应的实验结果及分析在下面给出.

斜坡力跟踪与恒定力保持的结果在图8所示,其中Fdes是系统期望的接触力,Fmes是使用机载力传感器实际测量的接触力,Fcal是根据姿态角由式(18)关系计算得到的接触力.分析图中0∼10 s的曲线可知,系统对斜坡力的跟踪响应较快,在跟踪过程中存在的数值波动则是由飞行平台振动引起的;10∼30 s的曲线显示系统可以在一定精度范围内保持期望的恒定力,且没有稳态误差.

图8 斜坡力跟踪与恒定力保持Fig.8 Ramp force tracking and constant force control

将图8所示的接触力Fcal与Fmes分别与期望接触力Fdes求偏差,结果显示在图9中.求出接触力误差∆Fmes=Fmes−Fdes和∆Fcal=Fcal−Fdes的均值与方差,如表2中所示.对比分析可知,∆Fcal的均值为0.0353 小于∆Fmes的均值0.1328;且∆Fcal的方差为0.0438小于∆Fmes的方差0.0867.这是由于力传感器中的感压应变元件在工作过程中存在低带宽、大振动噪声以及存有迟滞误差等缺点,从而导致其测量力结果存在较大偏差.而飞行器姿态是由IMU和磁罗盘等多种高带宽低延时的运动传感器测量并经数据融合得到的相对精确的姿态信息,并且由式(18)对应的力关系直接换算得到,所以从数据来看获得接触力的结果更可靠一些.

图9 接触力的实时误差Fig.9 The real time contact force error

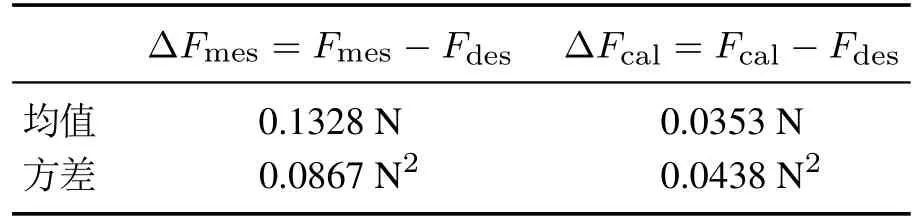
表2 接触力的误差分析Table 2 The error of contact force

由图8和9显示的实验数据结果来看,恒定力控制仍然存在一定的误差,以下对其原因进行深入的分析.对于旋翼飞行器系统来讲,本身是依靠多个螺旋桨高速旋转压缩空气产生动力,由于周围气流不稳、各个电机和螺旋桨不能保证性能和物理参数绝对的一致以及电压不恒定等因素,使得实际飞行器存在无法避免的振动,导致自身定位精度相对较低,即使是在动作捕捉系统中的位置控制精度最高可达±2 cm.自由悬停飞行状态下的每个电机转速也都不是恒定值(通常有大范围的动态变化).当在飞行器上加载机械臂进行接近环境的接触作业时,气流扰动等因素更加明显.对于一般的工业机器人,由于具有基座固定、伺服系统高带宽、优化的结构设计等优势,其末端位置控制精度可以达到亚毫米量级.而飞行器位置控制精度与之差2个量级,进而基于飞行器位置来控制接触力的效果,确实不能与工业机械臂力控制效果相比较,因此在力控制实验结果上就自然显示出相对较大的波动和误差.

根据本文的方法,飞行器x方向的期望位置会根据期望接触力做出相应调整,其曲线如图10 所示.可以发现,当机械臂接触环境位置为xreal时,只要在x方向上期望力Fd不为0,对应x位置就会存在相应的偏差,为xdesd−xreal.由于在y与z方向上没有进行接触力的控制,所以对应这两个维度的实际位置yreal和zreal一直保持在期望值ydesd和zdesd附近,其位置控制精度与自由悬停飞行时精度一样都是±0.03 m.

图10 飞行器位置变化曲线Fig.10 The real time position variation

在接触力控制过程中,期望俯仰角θd是由式(19)计算得到,并且将其输入到姿态子系统中进行跟踪控制.斜坡力对应的俯仰角曲线在图11显示,其中:实际俯仰角是θreal(对应图中pitchreal),期望俯仰角是θdesd(对应图中pitchdesd),且恒定力对应俯仰角是−0.218 rad.而滚转和航向角度值一直在零值附近波动,这是因为只是在无人机前向方向上有接触力控制,其他方向上没有接触力,所以无人机的滚转(对应图中roll)和航向(对应图中yaw)是自由飞行状态下的表现,且控制精度依旧为±0.03 rad.

图11 飞行器姿态变化曲线Fig.11 The real time attitude variation

对于飞行机械臂进行的接触作业,接触力最终还是由无人机平台来提供.对于斜坡力跟踪和恒定力保持的过程中,无人机总油门升力的变化也展现出与之对应的曲线,如图12所示.油门曲线常使用0∼1之间的数值来表示,图中0∼10 s的曲线对应是斜坡力跟踪时候的油门变化,10∼30 s的曲线对应是恒定力保持时候的油门变化,可见此时油门保持在0.565值附近.

图12 飞行器油门量变化曲线Fig.12 The total thrust curve of UAV

本文所附带的视频展示了所设计的单自由度飞行机械臂系统接触墙壁的实验,展示了飞行机械臂接近环境、接触力控制和返回3个场景,其中力控制实验包含斜坡接触力跟踪和恒定接触力保持2部分内容.

5 结论

本文首先从理论上证明了基于状态反馈控制器的闭环无人机系统表现出与弹簧-质量-阻尼系统一致的动态特性.并且基于推导的模型和阻抗控制思想,详细介绍了飞行机械臂系统不使用力传感器的接触力控制方法,同时分析了系统稳定性.继而开发了单自由度飞行机械臂系统用于方法的验证.最后的飞行接触力实验结果证明了本文所提出接触力控制方法的有效性以及所开发系统平台的可靠性.

下一步的研究工作将集中在多自由度飞行机械臂系统的接触操作方面.考虑到非结构化环境中的飞行操作,因此环境感知的问题也是未来工作的关注点.