一个不等式猜想的深入探讨
湖南省绥宁县瓦屋唐镇瓦屋梅坪小学
从启发式教学模式角度,对一个熟知的数学命题,引导学生做出大胆“类比、猜想”,并启发学生分析证明思路,进行论证,无疑是值得赞扬的教研探讨模式之一.许多数学教师在教学及教学研究中提出这种“类比、猜想”,使用“大胆猜想、细心求证”方法以锻炼和提高学生创新思维能力.文献[1-5]对2009年《数学通报》第十期问题1818 进行了研究.针对问题1818,施刚良老师等[1]提出如下类比猜想.
猜 想1[1]设i >0,i=1,2,··· ,n,n ∈ℕ,n ≥则

猜想2[1]设k,n ∈N,ai >0,i=1,2,··· ,n,n ≥3,k ≥2.则

这时猜想2中的不等式转化为,

近年来,作者未见有关文献报道解决这两个猜想.本文的目的是证明在一些情况这个猜想成立,而在另一些情况猜想不成立.
注记1由于(2)是(1)的推广,因此猜想2是猜想1的推广.
注记2当n=3时,文[1],[2],[4]已经证明(2)成立,文[3]给出证明了.当n=3时(2)的一个推广形式.我们注意到当n ≥4,k=2时,(2)不成立,所以n ≥4,k ≥2时猜想2 不成立.事实上,当mi=t >且t →+∞时,我们有
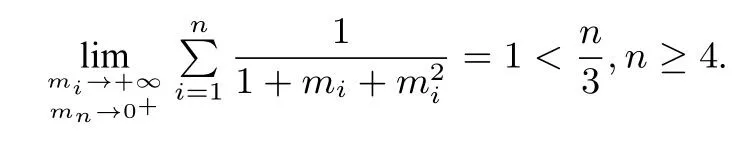
故当mi >0(i=1,2,··· ,n-1)很大,而mn >0 很小时就有
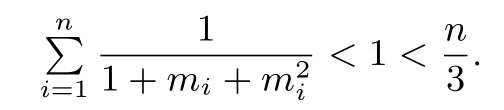
故(2)当n ≥4,k=2时不成立.例如取n=4,m1=m2=m3=10,m4=0.001,我们有m1m2m3m4=1 但是
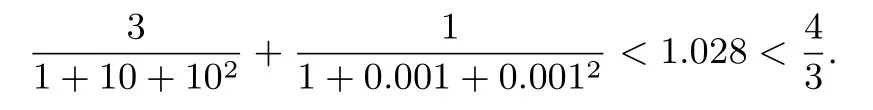
类似地,当k ≥1,n >k+1时,我们有

因此当n ≥k+2,k ≥1时(2)不成立,所以此时猜想2也不成立.
定理1设n,k为整数,n ≥k+2,k ≥2,mi >0,i=则
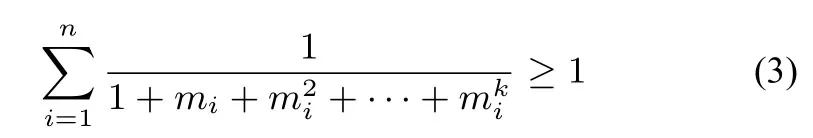
等号成立当且仅当m1→0,mi →+∞,i=2,··· ,n.
证明容易知道有下确界α.所以对任意

于是对任意t >1 有从而
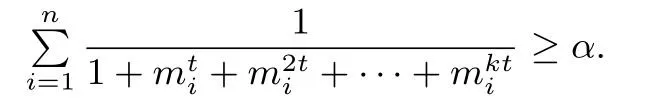
取t →+∞则立得α ≤1.
当n ≥k+2时,我们考虑

其中被减数中有n(k+1)n-1项,合并同类项后常数项是n,其他项为
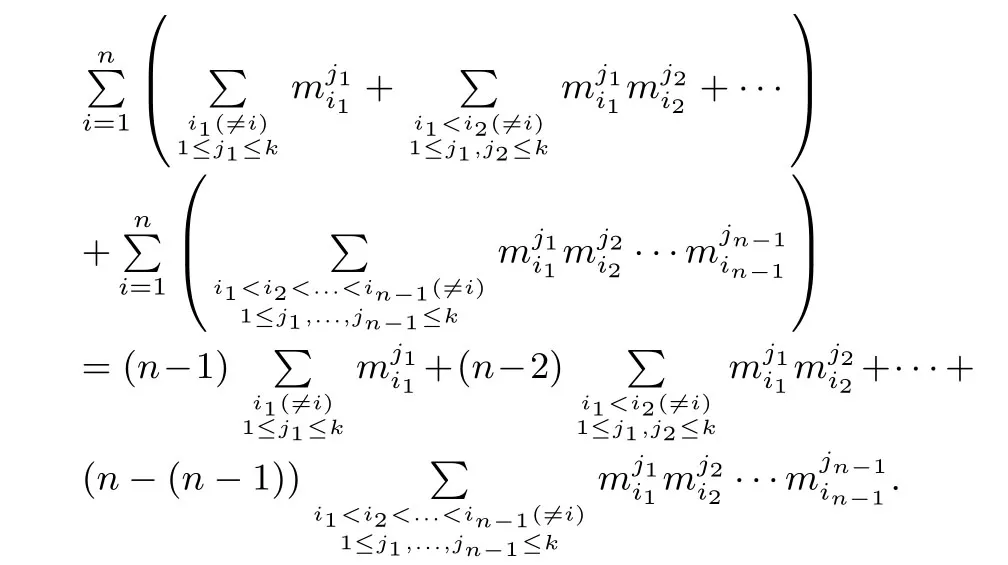
共计
其中减数中有(k+1)n项,合并同类项后常数项为1,其他项为

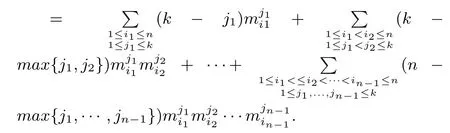
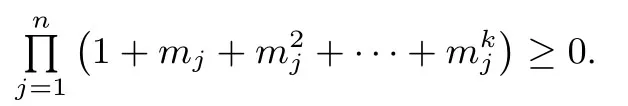
推出(3) 成立.容易看到(3)中等号成立当且仅当m1→0,mi →+∞,i=2,...,n定理证明完毕.
定理2设n,k为整数,2≥n ≥k+1,2≥k,mi >则
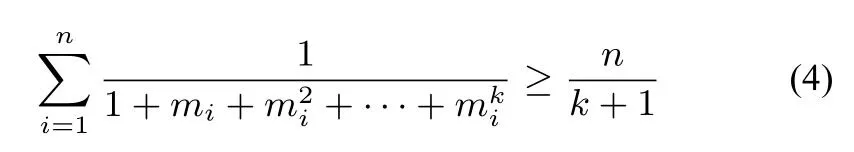
证明容易知道有下确界α.所以对任意

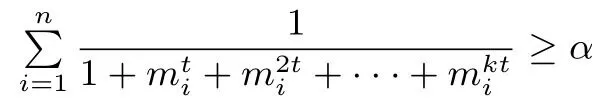
取t →0 则立得
当2≤n ≤k+1时,我们考虑

其中被减数中有n(k+1)n项,合并同类项后常数项是n(k+1),其他项为项.



这样,被减数减去减数为
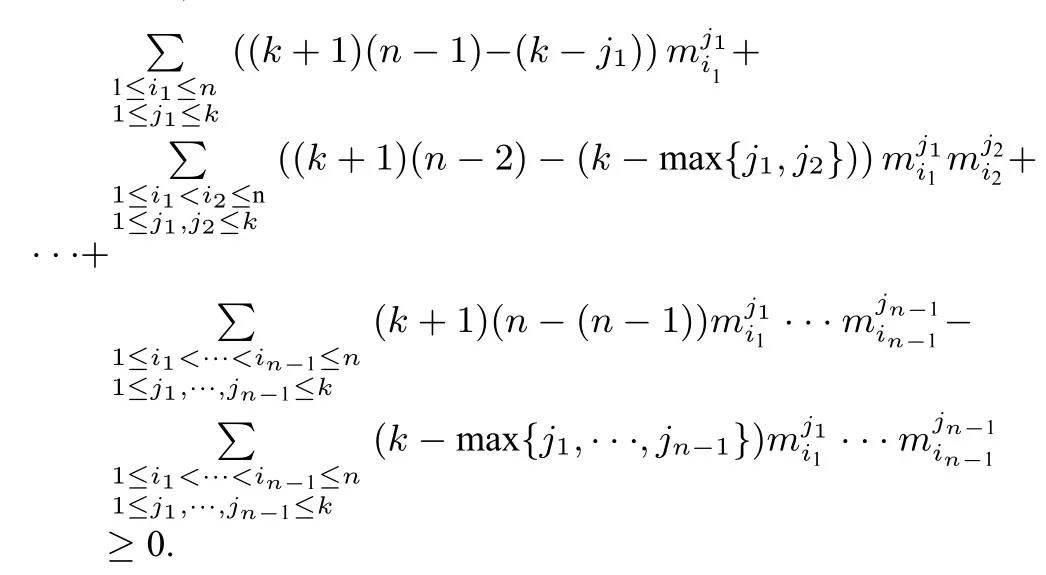
推出(4)成立.容易看到(4)中等号成立当且仅当xi=1,i=1,2,···,n.定理证明完毕.
定理3设x,y >0,xy=1,k ≥1.则

证明作辅助函数
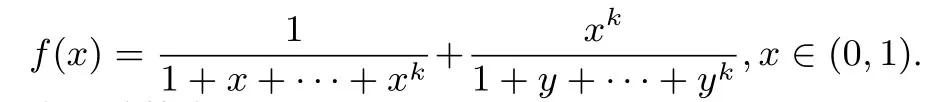
容易计算当x ∈(0,1)时,有

定理4设n ≤2,k ≤1为整数,xi >0,i=则
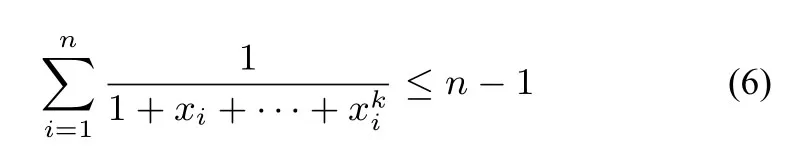
证明由于

只需证明
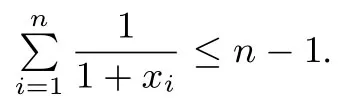
容易推出

而后者显然成立.又

所以(6)中等号成立当且仅当xi →0,i=1,2,··· ,n -1,xn →+∞.定理证明完毕.
定理5设n,k为整数,2≤n ≤k+1,k ≥2,ai >0,i=1,2,··· ,n.则
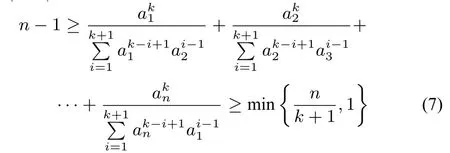
证明取则于是(7)等价于
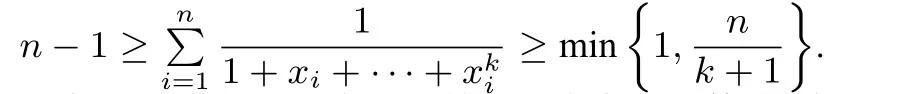
由定理1,定理2和定理4 结论得本定理不等式.定理证明完毕.

