温故知新复而不重*—-“相似”单元复习课的教学与思考

广东省东莞市东莞中学松山湖学校

裴光亚老师指出：“复习要重复又不能复重.”江苏的石树伟老师也提出：“单元复习应当复而不重，温故而知新”，那么单元复习课教学又应当如何处理好温故与知新的平衡，把握好重复的度呢?下面，结合本人2019年1月在东莞市初三数学复习研讨会上执教的人教版九年级下册“相似”单元复习课教学，谈一些个人的思考，与大家交流.

1 教学案例

1.1 教学目的

(1) 熟练掌握相似三角形的性质及判定方法，从相似基本图形的角度，进一步加深对相似知识的理解；

(2) 进一步体会分类、模型等数学思想在相似问题中的运用.

1.2 学情分析

本节课是“相似”一章的单元复习课教学，大约二个星期前，学生才开始进入相似的学习，现在刚结束本章内容的新授课教学，整体还处于“初学较新”的阶段，因此，对于相似知识的理解还不够深入，许多同学还没有很好地建立起相似知识的结构框架，特别是对相似和其他数学知识之间的关联体会不深，缺乏综合运用相似知识的能力，对于问题中所涉及到的分类思想、函数思想及模型思想等都还缺乏有深度的自我建构.从温故与知新的角度，本节课的复习教学应当是以温故为主基调，在此基础上求思维的新经验，知识的新架构.

1.3 教学过程

1.3.1 自主梳理，结构展示

教师：我们课前布置了请大家梳理《相似》这一章的知识结构，下面大家在小组内交流一下，稍后我们请两个小组派代表给大家分享.

学生1：(投影展示小组的知识结构框架图)本章的主要内容有相似图形、相似三角形、位似，其中相似三角形的性质与判定我们认为是最为重要的部分，对于判定，我们梳理出五种方法，分别是二角相似、二边及夹角相似、三边相似、平行相似、斜边与直角边相似，这些主要是类比三角形全等得来的.

学生2：生1的梳理重点很突出，我想补充一下基本的相似图形，(展示自己的知识结构框架图)有A型、斜A型、X型、子母型等，并在这些基本图形中，我们要特别注意对应边.

图1

教师：两个小组的展示非常有特色，条理清晰，重点突出，结构框架图做得很好.本章的学习正是利用了类比思想得到了相似三角形的判定定理，同时课本内容编排从“图形相似——三角形相似——位似”，这个次序也还体现了“从一般到特殊，从特殊再到一般”的思想.相似的兼容性很强，可以与很多知识组合，因此，本章的学习，还要特别注意基本图形的总结与运用，我们本节课的复习就从基本图形开始.

评析 复习首先是重复，梳理本章的知识结构，这是本章学习完之后的重复，但又不是纯粹的知识罗列，在重复之中，包含有学生个体自主梳理知识时，对章节知识体系整体的认识，通过他们对知识的重组、编码、重难点遴选展示，一方面可以激发学生的复习热情，培育他们的创新意识，另一方面，也可以折射出他们系统思维的理解层次.

1.3.2 问题引路 动态延伸

问题1如图2，ΔABC中，AB ＜AC，点P为AB边上一点，画一条直线PQ与AC边交于点Q，使你可以怎样画?

图2

学生3：过点P画PQ//BC，所得到的两个三角形就相似.

学生4：生3 画的实际上是正A型，还有一种画法是反A型的，如图3，此时，AP与AC对应.

图3

教师：很好，这里只说“ΔAPQ与ΔABC相似”，但并没有指明需要怎样对应，所以我们需要把二种情况都考虑到，下面我们继续添加一种情景来进一步研究.

问题2在问题1中，如果AB=8cm，AC=10cm，点P从A点出发，以2 cm/s的速度向B点移动，点Q从C点出发，以1 cm/s的速度向A点移动移动.若P,Q同时出发，当其中一点到达端点时，另外一点也随之停止运动.设运动时间为ts，那么t为何值时，ΔAPQ与ΔABC相似?

师生活动：学生小组研讨，核对答案，纠正或补充解题过程，教师巡堂，指导，搜集有意愿展示讲解小组的解答.

学生5：根据题意，我们可以知道AP=2t,QC=t,AQ=10-t,我们需要分两种情况进行讨论正A型，即代入求得就是反A型，即代入求得所以，当时，这两个三角形相似.

教师：说得很好！的确需要分两种情况讨论，但在区分这两种情况时，如何表述更恰当?

教师：补充得很好，在分类时，我们一般都是以边或者角来作为标准进行讨论的.那么，这两种情况，哪种情况先发生?

学生8：正A型.教师动态呈现点P,Q的运动过程.

问题3：对于前面的第种情况，是我们需要特别关注的.我们已经知道，此时∠APQ=∠C，如果我们保持这个关系不变，将PQ向下平移，当点P运动到点B时，AQ长又是多少?

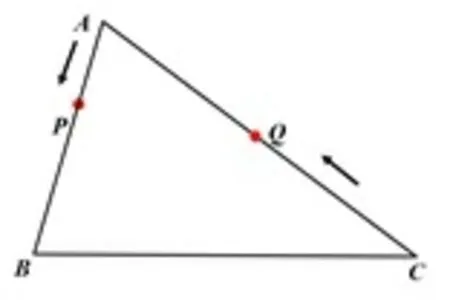
图4

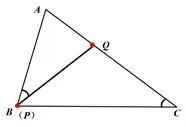
图5

学生9：当点P运动到点B时，一样的有△APQ ∽△ACB，由相似得到等比式，代入相关数据，即可求得

教师：非常好！其实，这时候图形中包含的就是我们所说的子母型相似.

评析通过问题1的画直线，问题2的动点分类讨论，到问题3的求值，一连串的数学活动，围绕着基本图形正A型、反A型、子母型相似在不断地重复，这就是温故，但也不是简单的重复.温故中，学生已有的知识经验和活动经验，借助于具体问题情景，在不断地更新，对相似基本图形本质理解和具体情景下的灵活应用经验也在不断地生长.

1.3.3 知识综合 模型提升

问题4在上面的图5中，如果有AB=AC，点P(不与B点、C点重合)在BC边上运动，点Q在AC边上，保持∠APQ=∠C.如图6，

(1)找出图中的相似三角形，并说明理由；

(2)若AB=8,BC=6,BP=x,CQ=y,求y与x的函数关系式，并求当x为何值时，y有最大值?

(3)在第(2)问中，当y取最大值时，请画出图形并判断ΔAPQ的形状.

师生活动：学生小组研讨，成员相互核对答案，纠正或补充，教师巡堂，指导，并搜集典型解答，7分钟以后，师生交流.

学生11：从直观上看，ΔABP∽ ΔPCQ，因为AB=AC，所以∠B=∠C,再找一个条件，因为∠APQ=∠C,所以，∠APQ=∠B，同时∠1+∠3=180°-∠B，∠2+∠3=180°-∠APQ，所以∠1+∠3=∠2+∠3，得到∠1=∠2，这样就证明相似.

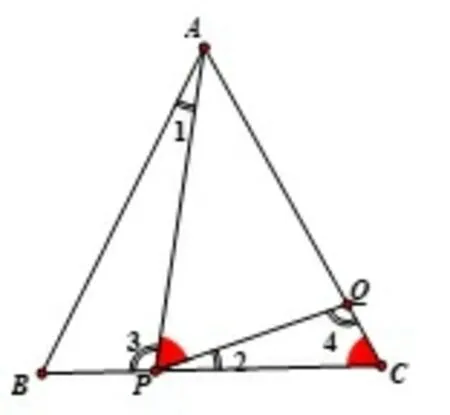
图6

教师：小组的同学还有要补充的吗?

学生12：还有ΔAPQ∽ΔACP，因为∠APQ=∠C，还有公共角，就可以得到相似.

教师：很好！这第二组相似其实就是我们前面所说的子母型，只是隐藏得很深，发现起来不容易.这一组的同学善于发现，表现很优秀.

学生13：由相似就可以得到等比法，代入数值整理，就可以得到用公式就可以得到当x=3时，y有最大值为

学生14：我觉得要加一个a ＜0时，因为当a ＜0时，y才有最大值.或

教师：好，思维很严谨，补充得很有必要，这是跟二次函数知识相联系的.

学生15：由第(2) 小题，我们可以得到x=3，也就是BP=3，P为BC中点，所以AP ⊥BC，由第(1)小题，可以得到PQ ⊥AC，ΔAPQ为直角三角形.

教师：很好，但老师想知道，为什么P是中点时，就有PQ ⊥AC呢?

学生15：因为等腰三角形的三线合一.

教师：很好！在这个图形中，有两个三角形非常引人注目：ΔABP,ΔPCQ(教师彩笔描绘图形)，它们是相似的，而且它们的位置呈现出在同一直线上有三个等角.这个图形有个名称：一线三等角，在相似界，很有地位，这里我们有一个微课，大家一起来看看.(播放“一线三等角”微课视频)

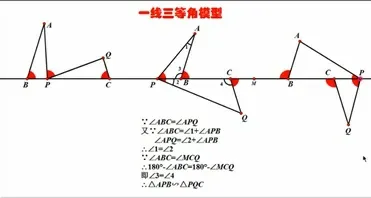
图7

教师：在微课的三个图之中，变化的是什么?

学生16：P点的位置在变化.

教师：那不变的又是什么呢?

学生17：三个角，在一条直线上有三个等角.

教师：还有没有不变的?

学生18：相似.

教师：对，在动点P变化的过程中，总存在着两个三角形相似，这就是变化之中的不变性，这就是模型带给我们的价值和意义.

评析问题4是建立在重复相似三角形判定方法、重复二次函数相关知识基础之上的综合性问题，三个小题的连续探求，联结了相似与二次函数及最大值问题，体现了相似与其他知识之间的横向联系.单元复习中展示这种联系，毫无疑问是有必有的，因为这就是将本章知识纳入整个数学系统，是对本章数学知识的精致.对于学生，有对以前所学知识的重复，但显然，这种重复不是单调的重复，而是数学知识整体的进一步综合.

1.3.4 课堂小结 相似展望

教师：现在让我们一起回顾一下，本节课我们遇到了哪些基本图形?

学生：A型、反A型、子母型、一线三等角.……教师：又用到了哪些思想方法?

学生19：类比、分类讨论等.

教师：相似不是独立的，它还可以与其他数学知识相联系，融合成许多新的问题，在初中数学体系中是兼容性比较强的一部分，比如，它可以与函数的知识、三角形、圆等知识综合.

评析章节复习跟概念教学一样，都要有章节知识的精致.就是将本章知识，纳入到更大范围的知识体系，使学生不仅看到树木，也能看到森林.本节课的小结，一是紧扣基本图形，以图形来联结相似三角形的判定，二是追问数学思想方法，促进学生更深一层地理解把握本章核心内容.

2 教学反思

2.1 温故求新

温故而知新，温故是单元复习的起点，也是知识梳理的基础，知新是单元复习的目标，在章节单元的背景下，对以前的知识有更新的理解和认识.温故，不是把以前的题拿出来重新做，不是把以前的知识搬出来重新复述强调，而是通过巩固强化对基本知识、技能的深入理解，关注学生平时易出现的错误，查漏补缺，运用知识技能解决具有典型结构特征的问题，促使学生在自主整理和综合应用的过程中对所学知识进行精细加工和深度理解，从而完善学生的数学认知结构.知新，是将重点知识、核心知识，通过变换以不同的背景、设置不同的问题、不同的解答思路等来呈现新意，在达成基本目标的基础上，深入挖掘基本数学知识所蕴含的数学思想方法.单元复习贵在知新，通过知识的重组、拓展、深化，进一步发展学生的数学思维能力和解决稍微复杂问题的能力，提升学生的数学素养.

2.2 变式求新

本节复习课的设计，在温故梳理知识之后，就从一图开始，预设一个一个变式问题，逐层递进.问题1的画直线找相似是基本问题，到问题2的动点找相似求线段长是老问题新情景，再到问题3的“子依母怀”的子母相似，这是运动的持续，问题4是运动的进一步深化，图象的进一步复杂，所提炼出的“一线三等角”相似模型等，是学生相似基本图形的新增长，这一系列的问题变式，配以图形变式，犹如一根长线一样，将学生新授学习过的相对零散的知识串联在一起，形成一个有序的彼此联系的有机整体，使整个复习变得简约、清晰而明快.

2.3 开放求新

温故与知新，还应当体现在复习选题上.复习课的教学，在唤醒并梳理已学知识的同时，更应当设计一些开放题，让学生在“炒冷饭”的过程中，品出“新味”.在课例中，梳理章节知识框架是开放的，问题1 设计相似三角形的直线是开放的，问题4 寻找图中所有的相似三角形也是开放的，这些开放问题，让学生的学习更多一份主动，课堂更多一份生机、活力与可能.虽然起点并不高，但都可以极大地激发学生的参与兴趣，有助于培养他们的发散性思维能力和创新思维能力，学生的解答，表现出不同层次、多种水平的解答方案，他们相互补充，共同激活彼此已有的经验，促进提高复习的效益.

2.4 微课求新

在课例中，嵌入了“一线三等角”的微视频，这是在网络上找的视频，但我们又重新请了班上的学生协助进行了录制.虽然时长只有2分钟，但它的出场果不其然地吸引了学生，因为是他们熟悉的同学的声音，讲解也很清楚明了，毫无疑问，这种新的设计，既体现了利用信息技术创新教学的时代特征，又极好地点拨到学生的思维，使他们聚焦在动态的变化中，观察捕捉出变化中的不变性，抽象出新的数学模型.

3 最后的话

复习本是仁者见仁，智者见智的，但温故知新应当是永远的主题.“温故”与“知新”并非是平行并列的两件事.对于学生学习与教师教学而言，新知识是旧知识的拓展，而旧知识是新知识的基石.“知新”是关键，本节课的复习，围绕章节核心知识，通过变式、设计开放问题、微课等多种形式求新，使复习的学习过程在学生的温故之中，实现对数学知识方法的再认识、再领悟和思维再提高，这样的复习，就是以温故为起点，以知新为目标，使温故与知新成为一个相互交融的有机整合，实现数学思维的深度生长.