信息技术助力直观想象核心素养提升——初中数学解题教学实践例谈

广东省广州市花都区圆玄中学

直观想象素养出自教育部最新修订的《普通高中数学课程标准》，是高中数学六大核心素养之一，也是初中数学素养的重中之重.直观想象借助几何直观和空间想象感知事物的形态与变化，而信息技术的合理引进能让这种感知达到极致，学生能在枯燥，晦涩的数学学习中领略直观想象带来的生机和活力，很多看似无从下手的数学问题若借助恰当的信息技术手段助力学生的直观想象，便能轻松获得解决问题的思路.初中数学解题教学中，信息技术的使用对于提升学生的直观想象素养有着不可替代的作用.

1 文字图像化，为直观想象提供载体

直观想象的载体是图形.华罗庚先生曾说：“数缺形难以直观，形缺数难以入微”.数与形结合是一种重要的数学思想，它在初中数学解题教学中应用广泛.初中学生往往对含数学术语的文字和符号有畏惧心理，尤其是大段的，长篇幅的更是如此.利用信息技术软件中的作图工具将这些看似枯燥乏味的文字图像化，为学生直观想象提供可视材料，让数学问题变得形象，有亲和力，才符合学生的认知心理特征.数学课堂上经常合理使用类似的信息技术手段，既增添一些有价值的数学元素画面感，吸引学生注意力，又能让学生积累直观想象经验，为快速解题打下坚实的基础.

下面是解题教学的课堂实录节选片断：

九年级数学题：小红在自家楼房窗户处测量楼前一棵树的高，现测得树顶处俯角为45°，树底处的俯角为60°，楼底到大树的距离为20 米，请帮小红计算树高.

课堂状况当看到没有配图的文段时，很多学生表现显为无法集中注意力思考，或者不知从何处入手思考，全班呈现出躁动状态.

学生自己完成配图后，教师与学生一起利用PPT作图软件将题目内容画出图1展示于多媒体平台.

图1

课堂状况看着枯燥的文字演变成多彩的几何图形，学生一片唏嘘，对比自己配图，他们震撼作图软件功能的强大，学生很快沉浸于图形的分析之中，课堂呈现勃勃生机.

上例充分显示出运用信息技术手段在将数学文字信息图像化方面的优势，迅速，便捷，准确，形象，仿佛赋予题中文字以生命，为学生的直观想象提供可视载体，为进一步进行数学思考搭建了良好平台.

教学实践证明，在利用恰当的信息技术手段将文字信息图像化中，不仅表现为演变成几何图形的优势，也表现出快速，准确地将文字信息演变成函数图像的优势，学生的直观想象素养在一次次类似的实践中逐步得到培养，利用这些图形或图像去感知，理解和分析数学问题时更容易找到突破口.

2 动态演示为直观与想象架设桥梁

很多数学问题的解决依赖于直观和想象的融合，对于初中数学某些类似于压轴的问题，要想准确地找准解题切入点，促进探索和形成正确的论证思路更需要这种融合，这类问题往往难度大，信息多，思维坡度陡，引入几何画板将题中信息动态演示，便能轻松自如地架设直观与想象的桥梁，不仅有图形，还让这些图形根据题中的条件动起来，将原本难以想象的画面形象地摆在学生面前，让学生的感官与思维一起被吸引，这种看得见的变化降低思维难度，可能引领学生发现规律，利于帮助学生顺利找到解题思路.

下面是解题教学的课堂实录节选片断：

九年级数学题：如图，已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG,CG.

(1)直接写出线段EG与CG的数量关系；

(2)将图2-1中ΔBEF绕B点逆时针旋转45°，如图2-2，取DF中点G，连接EG,CG，(1)中的结论是否仍然成立?写出你的猜想并加以证明.

(3)将图2-1中ΔBEF绕B点旋转任意角度，如图2-3所示，再连接相应的线段，问(1)中的结论是否仍然成立?

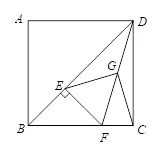
图2-1

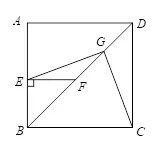
图2-2

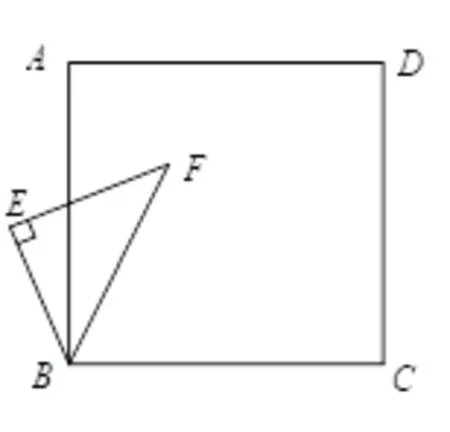
图2-3

课堂状况：第(1)小题直角三角形斜边上的中线基本图形一目了然，部分学生对于第(2)小题能利用现有几何图形构造需要的直角三角形斜边上的中线基本图形，教师运用几何画板将第(2)题的解题剖析图展示于电子显示屏，用彩色锁定为寻找解题切入点而构造的直角三角形，配着优秀学生美妙的思路解说，呈现于大家的眼前，集听觉，视觉于一体，大多数学生能较顺利地找准解题切入点，理清解题思路.

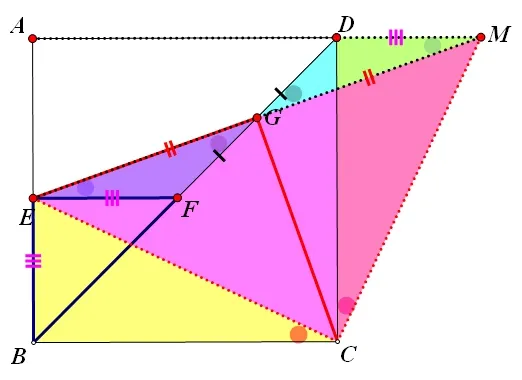
图3

优秀学生解说：图2中要证CG=EG，我们可以构造第(1)题中的直角三角形基本图形，首先利用中点，构造一对全等三角形(遇中点，构造全等三角形EFG和三角形MDG，如图3.这是常用的辅助线作法)，则EG是EM的一半，即点G是EM的中点.连结EC,MC，易看出CG是ΔECM的中线，只需要证得∠ECM是直角，则直角三角形斜边上的中线基本图形构造成功，易得EG=CG.

学生思考障碍：对于第(3)题中的“旋转任意角度”学生感到些许茫然，题中虽配旋转后的直观图，但因旋转的是任意角，第(2)小题中原本构造的基本图形无法显示，学生对着这图难以展开想象，几乎所有学生对找解题的切入点无从下手，学生深感此题难度太大.

教师应对对策：

先利用几何画板的动态功能通过铺垫降低学生的思维难度.先将原题图(1)中的三角形BEF作顺时针旋转45°后模仿前图解题.

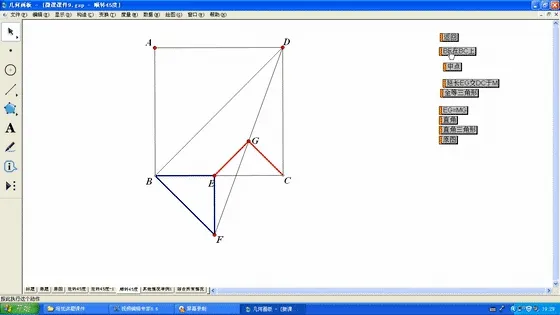
图4

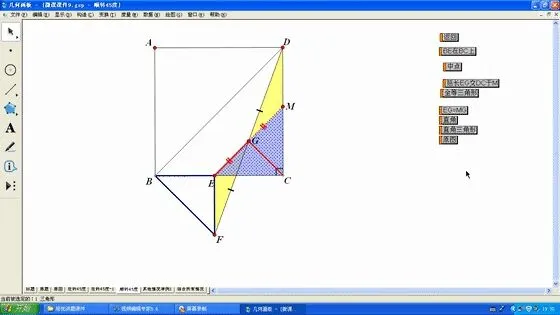
图5

再将三角形BEF逆时针方向旋转较小角度，动图落定瞬间即动态播放类似于前题构造直角三角形斜边上中线的基本图形的过程.

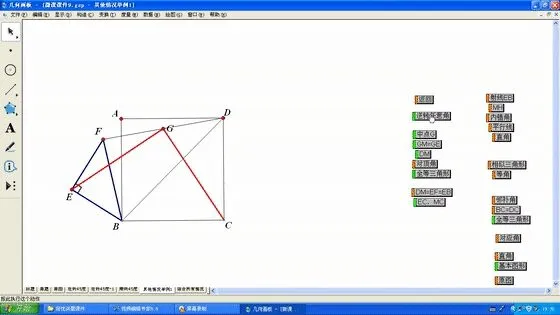
图6

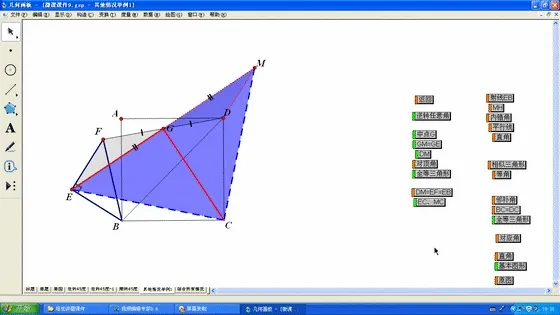
图7

然后将三角形BEF按顺时针或逆时针方向随意旋转较大角度，每个动图落定瞬间都动态播放构造直角三角形斜边上中线基本图形的过程，然后完整慢速播放旋转360度的全过程.

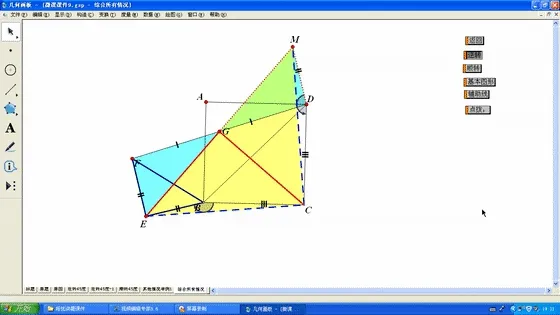
图8

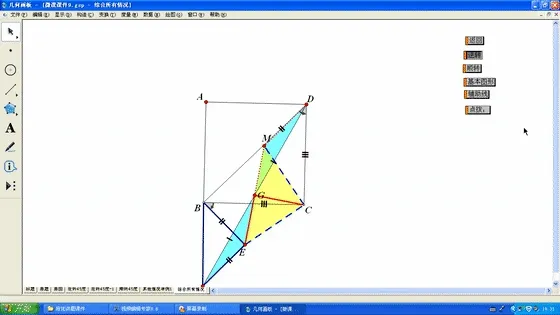
图9

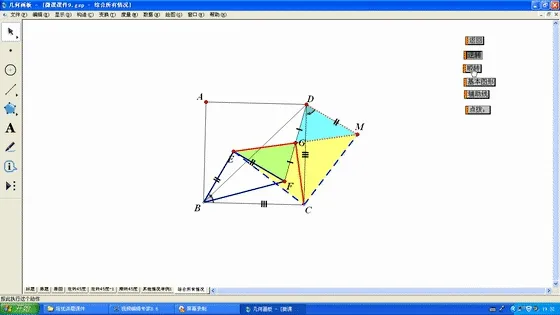
图10

其解题思路如下图：

本题是以旋转为背景的几何综合证明题，题中包含了较多的基本图形，涉及正方形的性质，全等三角形的判定与性质，直角三角形斜边上的中线性质等知识的理解与应用，比较复杂.思考问题的过程中需要借助直观与想象的结合，善于寻找或构造基本几何图形，并结合条件与结论，画出探寻证题思路的思维流程图，便可使思路清晰.解决这类几何问题的核心本质是在“变化”之中找“不变”.

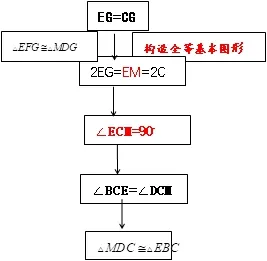
图11

上例教学中，教师使用几何画板动态演示，将原本难度大且不易想象的数学模型生动地刻画出来，确实利于有效降低题目难度，完美地将直观与想象融合，揭示解题规律，找准解题的切入点，促进学生顺利打开解题思路解决数学问题.

3 抓准解题能力的生长点，作图软件让直观想象绽放异彩

解题教学要避免就题论题，在高品质解题教学中，需要我们有一双慧眼抓准教学中蕴含的解题能力生长点，它是学生已有的解题经验，又是新的解题能力得以提升的本源，几何解题教学中，在这个生长点上引进恰当的作图软件，便能引领学生多方位直观想象，促使学生的思维更灵活，解法更多样.

九年级数学题：如图12，已知在圆O中，弦AB=AC,点P是∠BAC所对弧上一动点，连接PA,PB,PC.若∠BAC=60度，试证明PA=PB+PC.

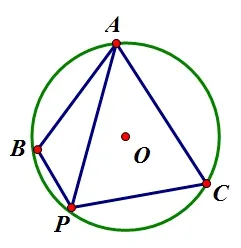
图12

证明两条线段之和等于第三条线段，通常是转化为证明两条线段相等.这是学生已有的解题经验，又是学生解题能力的生长点.转化为证哪两条线段相等?首选将三条线段变两条线段，有同学提议：要么截长，要么补短.该如何截长补短?此时运用作图软件，快速呈现学生截长补短的初步想法.有同学提议：“既然条件中有‘AB=AC,A,B,P,C四点在同一圆内’可以尝试用‘旋转’达到‘转化为证两条线段相等的目的’”.在遵循“转化为证两条线段相等”的大方向不变的情况下，学生能在短时间内通过图形表现自己不同于别人的想法，学生的直观想象在此刻绽放异彩.

课堂状况学生尝试添加辅助线，将其转化为证两条线段相等的情况.对照图形探寻证题思路.再小组交流不同的辅助线作法，以及不同作法的依据，大多数学生沉浸在探讨学习的氛围之中，课堂时而祥和，时而活跃.

作补短图如下：

图13

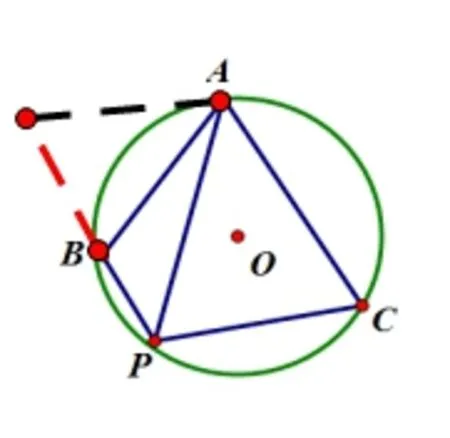
图14

作截长图如下：

图15

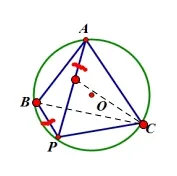
图16

旋转图如下：

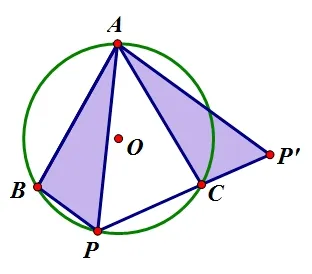
图17

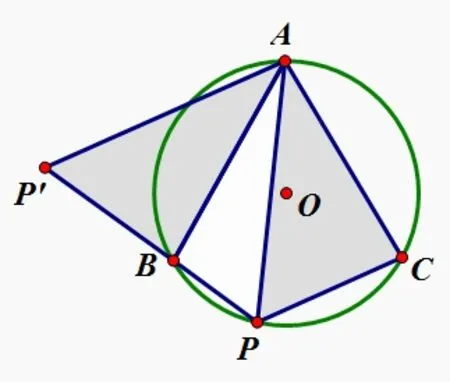
图18

剖析：作图软件的适时引入，快速呈现学生截长补短及旋转的各种情况，以转化成证两条线段相等为目标，从不同角度和方向考虑，尽可能多的引领学生的直观想象异彩纷呈.原本在前阶段跟不上课堂进程的部分学生随着软件作图画面的一一呈现，其思维被激活.

多角度，多方法，多层次的思考问题，拓展了学生思维的宽度和广度，确实能促使学生思维活跃，但我们要运用作图软件为学生提供施展想象的平台，几种情况下共性解题策略也逐步显现，学生的思维能力，解题能力在绽放的直观想象中得以提升.

既然解题能力的生长点是学生已有的解题经验，又是新的解题能力得以提升的本源，则在上述解题教学中，在学生已有的“将此类问题转化为证两条线段相等”的解题经验的基础上，将题中的问题或条件作适当改变，学生在解决新问题的过程中，从变中进一步提炼方法，发现规律，从“变”中发现“不变”，运用作图软件完成条件或问题的改变，无疑给学生的直观想象提供了便捷的工具，其解题能力也在这一过程中得到进一步提升.

学生对上例有如下变式：

变式：在四边形ABPC中，AB=AC,∠B+∠C=180°(或改为∠BAC+∠BPA=180°)，连接PA.若∠BAC=60°，试探究PA,PB,PC之间的数量关系.

把圆的背景去掉，将题中“圆的内接四边形对角互补”知识点置换成∠B+∠C=180°.作图软件的隐藏功能发挥便捷作用.

变式：将原题中∠BAC(旋转角)= 60°改为90°,120°,其他不变.

这种变式由作图软件帮助呈现学生的想象，既节约学生的绘图时间，又帮助学生打开眼界，让思维过程中的“去表存本”更加清晰明朗.

在上述过程中，作图软件的应用将学生的发散思维发挥得淋漓尽致，再次让学生的直观想象绽放异彩，其解题能力得以生长.

初中数学解题教学中，恰当运用信息技术手段帮助学生构建数学问题的直观模型，学生运用多种感官协作学习，促进学生主动将抽象思维与形象思维结合运用.利用信息技术软件为学生的直观想象提供可视材料，化静为动，把学生理解中的难点动态演示，为直观与想象架设桥梁.解题教学中抓准学生解题能力的生长点，利用作图软件快速，准确，形象，生动地展示学生的想象，用图思考，数与形完美结合，确实能激活学生思维，学生的直观与想象素养在这一过程中也得以提升.