含隐藏吸引子的分数阶Sprott E系统动力学分析及投影同步
张盟琦,张宏立,王 聪
(新疆大学 电气工程学院,新疆 乌鲁木齐 830047)
混沌是非线性动力系统出现的一种随机现象,广泛存在于工程领域[1].混沌系统中,主要存在两种吸引子:自激吸引子和隐藏吸引子.隐藏吸引子具有与自激吸引子完全不同的动力学特征, 得到了学术界的广泛关注[2-5].文献[6]在Chua系统中发现了隐藏吸引子,并对其进行了动力学分析. 文献[7]构造了无任何平衡点的混沌状态,调整参数使4维忆阻自激振荡系统含有隐藏吸引子.文献[8]分析了一类具有隐藏吸引子的Jerk混沌系统,证明系统存在稳定平衡点. 文献[9]研究了高维非线性系统的隐藏吸引子.文献[10]研究了一种具有隐藏吸引子的分数阶混沌系统的动力学行为及有限时间同步.文献[11]对分数阶混沌系统进行了研究,主要集中在函数投影同步方面,使系统在不同阶次上实现投影同步.文献[12]对整数阶Sportt E系统的混沌动力学行为进行了研究,但未涉及分数阶.笔者采用分数阶时域求解的方法,对分数阶Sprott E系统的动力学行为进行研究,使用投影同步的方法设计控制器,实现同步控制.
1 分数阶Sprott E系统及动力学分析
1.1 分数阶微分概述
根据不同的研究背景和意义,分数阶微分赋予了多种形式的定义,目前使用较多的有Riemann-Liouvile、Caputo和Grunwald-Letnikov定义[13-14]. 在工程应用中,Caputo定义的物理含义更加明确,对分数阶微分方程初始值问题的描述更有意义,因此该文采用Caputo定义.
定义1Caputo分数阶微分定义式为
(1)
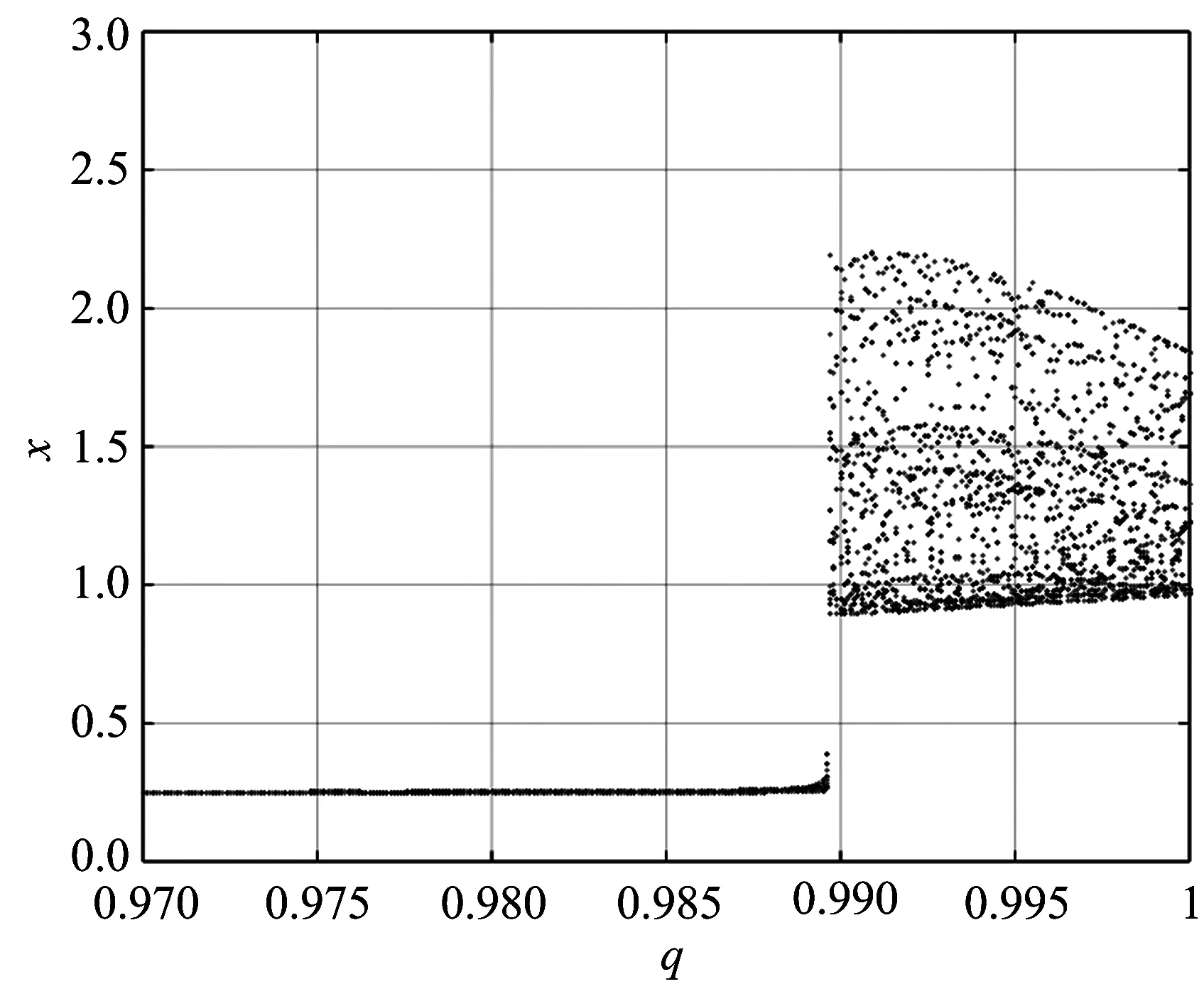
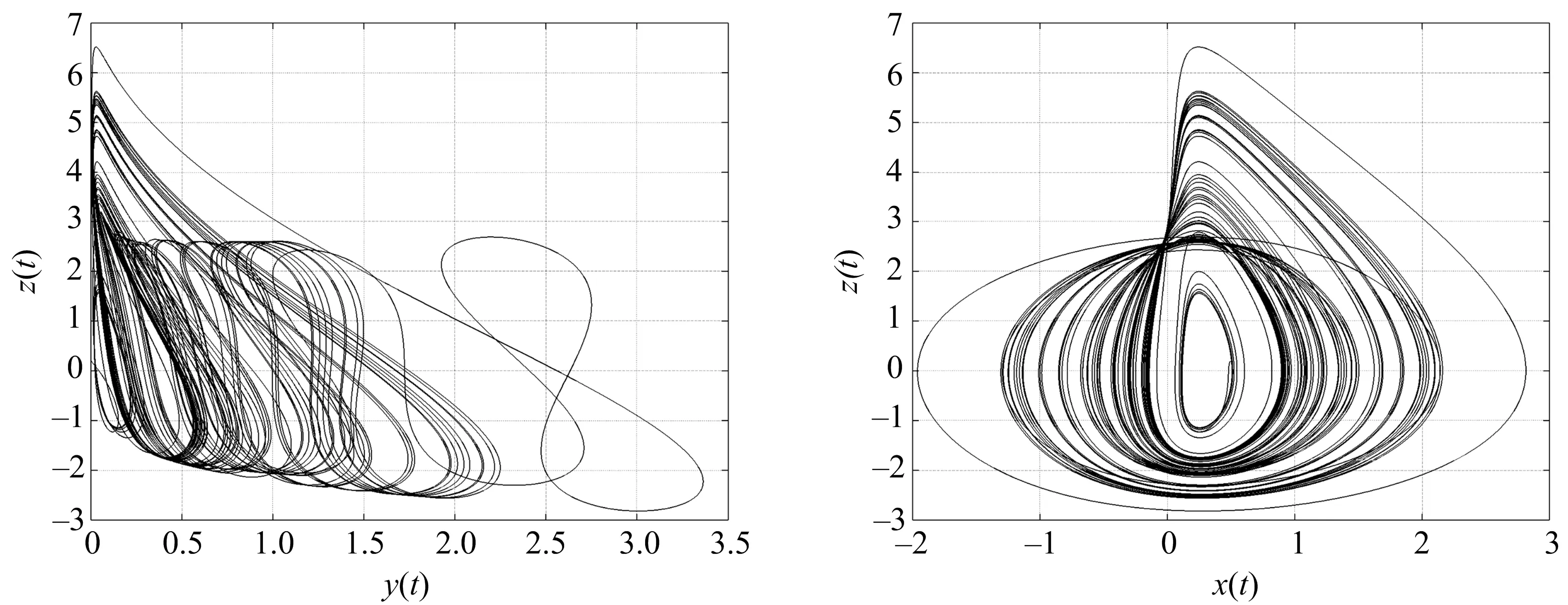
其中:q为阶数,n为大于q的最小整数,且n-1 令 (2) 分数阶微分方程可描述为 (3) 该方程的通解为x(t)=x(0)Eq(Atq),其中 (4) 整数阶Sprott E系统是最简单的3维混沌系统, 由2个2次非线性5项多项式组成,由J. C. Sprott通过计算机穷举法发现[15]. 整数阶Sprott E系统定义为 (5) 将整数阶Sprott E系统推广到分数阶,构造的含隐藏吸引子的分数阶Sprott E系统为 (6) 其中:a为系统参数;q为系统的阶次,且0 定理1[12]当a=0.005时,分数阶Sprott E系统(6)具有唯一稳定平衡点. 证明令式(6)右侧为0, 得到系统的平衡点方程为 (7) 解式(7)得到系统仅有的平衡点O为 (0.25,0.062 5,-0.08). (8) 在此平衡点,系统的雅可比矩阵为 (9) 令其特征多项式det(λI-J)=0,得到对应的特征值为 (10) 由式(10)可知,3个特征值均有负实部,可知该平衡点具有稳定性. 分岔图在观察系统参数变化方面独具优势,可直观显示参数变化轨迹.以阶次q为变量,取x(0)=0,y(0)=0.5,z(0)=0.2,进行数值仿真分析,得到状态变量x随阶次q变化的分岔图如图1所示. 图1 变量x随阶次q变化的分岔图 由图1可知,当q<0.987时,系统处于稳定状态;当0.987 通过相轨迹、时域图、庞加莱截面、功率谱进一步分析系统的非线性动力学特征.取仿真时间为500 s、步长为0.005,利用预估校正数值算法,得到系统的相轨迹如图2所示. 图2 系统的相轨迹 由图2可知,3维吸引子相图看起来杂乱无章但其中也有规律性.2维吸引子相图呈现如下混沌特性:单涡卷特性、伸展的螺旋运动和折返的单向运动,其吸引子的随机性主要表现为折返运动的不确定性,表明系统处于混沌状态.图3为系统的x时域图. 图3 系统的x时域图 从图3可看出,随着时间递增系统状态变量的变化看起来杂乱但其中也呈现有序的情形,可见系统处于混沌状态. 根据庞加莱映射,得到系统z=0的庞加莱截面如图4所示.从图4可看出,庞加莱截面由密集的点构成,对应着吸引子伸展的螺旋运动,具有分形结构的密集分布特征.取采样频率为0.2 Hz,仿真时间为500 s,得到系统的功率谱如图5所示.从图5可看出,功率谱是连续谱,且没有明显的峰值.根据庞加莱截面和功率谱的特征,可知系统处于明显的混沌状态. 图4 系统z=0的庞加莱截面图 图5 系统的功率谱 所谓投影同步是通过调整常数尺度因子,使响应系统和驱动系统实现完全同步,即各状态变量在相同比例下同步. 该同步方法具有不同于传统控制的优点,可对两种系统(驱动和响应系统)状态变量间的尺度因子进行任意调整. 笔者在文献[11]基础上,将Rossler系统和Sprott E 系统分别作为驱动系统和响应系统,设计控制器以实现同步控制. 定理2将Rossler系统作为驱动系统,其可描述为 (11) 其中:xd,yd,zd为驱动系统的状态变量;q=0.99. 将Sprott E系统作为响应系统,其可描述为 (12) 其中:xr,yr,zr为响应系统的状态变量;u1,u2,u3为非线性控制项;q=0.99. 存在控制器 (13) 使Sprott E系统与Rossler系统完全同步. 证明当a=0.2,b=0.2,c=5.7时,驱动系统出现混沌现象. 定义投影同步误差为 (14) 其中:α(t)为尺度函数.对式(14)两端求导得 (15) 整理得 (16) 引入如下Lyapunov函数 (17) 通过计算得 -e12-e22-e32≤0. (18) 为验证控制器的有效性,采用Matlab进行仿真.取h=0.005,T=200 s,α(t)=1.2,xd(0)=-1,yd(0)=-2,zd(0)=1,xr(0)=4,yr(0)=-4,zr(0)=4,得到系统误差、状态变量的仿真图,分别如图6,7所示. 图6 系统误差曲线 图7 状态变量 由图6可知,控制器使系统达到了稳定状态,且达到稳态所用时间短暂;5 s时误差系统就趋近零点并达到稳定状态.由图7可知,在控制器的作用下,Sprott E系统的xd和Rossler系统的xr在开始的一段时间略有波动,但4 s时就趋于同步; Sprott E系统的yd和Rossler系统的yr于2.8 s达到同步; Sprott E系统的zd和Rossler系统的zr于5 s达到同步.综上可知,设计的控制器具有有效性. 笔者将整数阶Sprott E系统推广到分数阶, 根据分数阶稳定理论,分析了系统平衡点的稳定性,证明了隐藏吸引子的存在.使用分岔图、相轨迹、功率谱、时序图、庞加莱截面,分析了分数阶Sprott E系统的丰富且复杂的动力学行为.基于分数阶投影同步控制理论和定理2,设计了控制器,对含隐藏吸引子的分数阶Sprott E系统实现了同步控制.数值仿真结果表明,该控制器具有有效性.该文研究结果对完善分数阶Sprott E系统、使其应用于混沌领域,具有一定的价值.1.2 系统模型及平衡点


1.3 动力学分析



2 分数阶系统的投影同步
2.1 投影同步
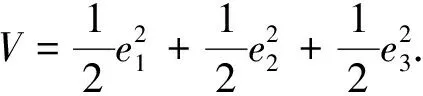
2.2 数值仿真


3 结束语

