关于Navier-Stokes-Voight 方程的若干探究

孙成峰， 刘星辰，焦小玉

(南京财经大学 应用数学学院，江苏 南京 210023)

论文主要研究Navier-Stokes-Voight(NSV)方程.文献[1-2]将NSV方程作为线性粘弹性流的运动模型提出，描述了Kelvin-Voight 粘弹性不可压流体的动力学.文献[3]将非粘性简化Bardina模型(非粘性确定NSV方程)看作带有周期边界条件的3维无粘欧拉方程的正则化,得到确定系统存在唯一弱解. 文献[4]研究3维无粘确定性Kelvin-Voight模型生成的半群具有有限维全局吸引子，得到了它的整体正则性. 当流体动力学中湍流的影响不能用确定的函数来描述，引入随机因素是合适而且是必然的.文献[5]研究3维可加噪声驱使下的随机NSV方程，得到其全局解的适定性，并在此基础上得出随机吸引子的存在性，给出了其Hausdorff维数的上界估计.

在此基础上，作者运用无穷维动力系统中的Galerkin逼近、Sobolev空间中的嵌入定理以及能量解的一致估计[6-12]，得出NSV方程全局解的适定性.最后，通过紧性理论及Chebyshev不等式得到随机方程不变测度的存在性.

1 预备知识

论文用u(x,t)=(u1(x,t),u2(x,t),u3(x,t))表示不可压流体的速度,p(x,t)表示压力.3维空间下的Navier-Stokes-Voight方程为

其中：Ω是一个带有光滑边界的有界区域；f(x)=(f1(x),f2(x),f3(x))表示给定的外部压力，与时间t相互独立；νΔu表示扩散项；ν>0是粘性系数；gk表示随机压力项.

定义v=(v1,v2,v3)，u=(u1,u2,u3)，且

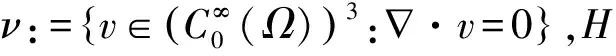
定义空间

其模为‖v‖1=‖v‖V=‖v‖.由Poincaré不等式，有V0=H,Pn:(L2(Ω))3→H. Helmholtz-Leray 即正交投射算子，定义

Aw=-PnΔw,∀w∈D(A)

为Stokes算子，D(A)=(H2(Ω))3∩V，A的特征向量wj构成H的标准正交基且满足

Awj=λjwj0<λ1≤λ2≤λ3≤….

定义

Hn=span{w1,w2,…,wn}，

并且令Pn是H到Hn的投射，定义Qn=I-Pn.

引理1定义一个非线性算子b为

b(u,v,w)=-b(u,w,v).

关于非线性算子b，有如下估计[2]

|b(u,v,w)|≤C‖u‖1/2‖u‖1/2‖v‖‖w‖,∀u,v,w∈V,

|b(u,v,u)|≤C‖u‖1/2‖u‖3/2‖v‖,∀u,v,w∈V,

|b(u,v,w)|≤C‖u‖‖v‖‖w‖1/2‖w‖1/2,∀u,v,w∈V,

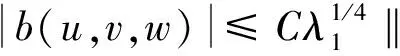
其中：C为实常数.

下面给出噪声强度项g(x,t,ω)的一些定义和条件.假设Y是任意一个可分的Hilbert空间，通过内积定义l2(U)，有

对任意赋范空间Y，g是一致Lipschitz连续的，如果存在KY，有

|g(x,t,ω)-g(y,t,ω)|≤KY|x-y|Y，

并且

|g(x,t,ω)|l2(U)≤KY(1+|X|Y)，

其中：KY与t和ω之间相互独立.

2 随机NSV方程的适定性

先对NSV方程做一个Helmholtz-Leray 正交投射

(L2(Ω))3→H,

在上述框架下，Navier-Stokes-Voight 方程可以写成

(1)

其中：B(U)=B(u,u)，b(u,v,w)=(B(u,v),w)，∀u,v,w∈V.压力项消失是由于在V′空间中p=0.

2.1 Galerkin系统及一致估计

定义1(Galerkin System) 如果∀v∈Hn，有(1)式成立，则随机过程u(n)∈C(0,T;Hn)是Galerkin 系统的一个解

〈u(n)(0),v〉=〈u0,v〉，

(2)

即

u(n)(0)=Pnu0.

(3)

为了表述方便，论文在下面的方程中均用u代替u(n).

定理1假设u是n阶Galerkin的一个解，并且

g∈Lipu(H,l2(H)),f∈L2(Ω;L2(0,T;V′))，

则

其中：CW是一个合适的常数，CW=CW(p,ν,λ1,T,|f|L2(Ω;L2(0,T,V′),KH)).

证明对(2)式运用It公式得到

(4)

(5)

所以，有

d(‖u‖2+α2‖u‖2)+d0(‖u‖2+α2‖u‖2)≤

对上式的最后一项，运用Burkholder-Davis-Gundy(BDG)不等式，有

将上式整理得

2.2 随机NSV方程解的全局适定性

定理2假设u是n阶Galerkin系统的解，并且

g∈Lipu(H2,l2(H)),f∈L2(Ω;L2(0,T;V′))，

则

证明对(2)式运用It公式得

d(‖u-α2Δu‖2)=2〈u-α2Δu,ut-α2Δut〉，

化简整理得

d(‖u-α2Δu‖2)+2ν(‖u‖2+α2‖Δu‖2)=

对b(u,u,Δu)进行估计，有

ν‖

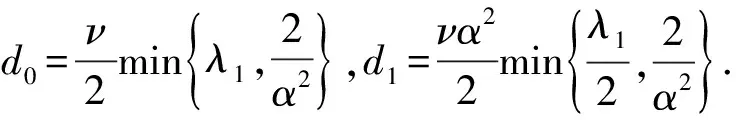
令h=min{d0,d1},则整理得到

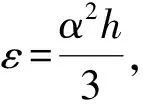
不等式两边取上确界,可得

对上式化简整理得

C(KH,α2)(1+‖f‖2+sup‖u‖2).

由定理1可知sup‖u‖2≤Cw，所以sup‖u-α2Δu‖2≤CW，u∈L2([0,(∞),H2) .

定理3(存在性) 存在一个u,B*和g*，u∈L2(Ω,L2(0,T;V)∩L∞(0,T;H2)) ，并且

B*∈L2(Ω;L2(0,T;V′))g*∈L2(Ω;H2(0,T;l2(H)))，

使得u,B*,g*对于任意试验函数v∈V，满足

(6)

u(0,v)=u0(v)，

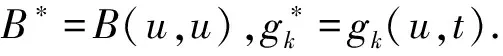
证明因为

所以序列{PnB(u(n))}一致有界，可以找到B*∈L2(Ω;L2(0,T;V′))，使得PnB(u(n))弱收敛于B*，有

设u满足(2)式，对于任意一个可测集E⊂Ω×[0,T]，v∈V，有

|(B(U)-PnB(u(n)),v)|=|B(U)-PnB(U)+PnB(U)-PnB(u(n))|≤

|((I-Pn)B(U),v)|+|(PnB(u-u(n),u),v)|+|(PnB(u(n),u-u(n)),v)| ≤

C‖(I-Pn)v‖(‖u‖6+‖u‖2)+‖(u-u(n))‖‖v‖(‖u‖+‖u(n)‖)，

两边取期望，得

另外，对于每一个k，有

其中

由控制收敛定理，得

d((‖Pnu-u(n)‖2eψ+α2‖(Pnu-u(n))‖2)eψ)+2ν‖(Pnu-u(n))‖2eψdt=

此处ψ为非正函数.

-2(Pnu-u(n),B*-B(un))≤2|(Pnu-u(n),B*-B(un))|=

(B(un-Pnu,Pnu)+(B(Pnu)-B(U))+(B(U)-B*),Pnu-u(n))≤

C‖u(n)-Pnu‖1/2‖(u(n)-Pnu)‖3/2‖Pnu‖+

((B(Pnu)-B(U))+(B(U)-B*),Pnu-u(n))≤

C(ν)‖Pnu‖‖u(n)-Pnu‖2+ν‖(u(n)-Pnu)‖2+(B(Pnu-u.Pnu)+

B(u,Pnu-u),Pnu-u(n))+((B(U)-B*),Pnu-u(n)).

定理得证.

定理4(唯一性) 假设u1,u2都是方程的解，并且在空间H中几乎处处u1(0)=u2(0)，有

P(‖u1-u2‖2+α2‖(u1-u2)‖2,∀t∈[0,∞))=1.

3 不变测度的存在性

证明假设u是方程的弱解，有

‖u‖2+α2‖u‖2=‖u(0)‖2+α2‖u(0)‖2-ν‖u‖2dt-2b(u,u,u)dt+

两边取期望，得

E(‖u‖2+α2‖u‖2)≤‖u(0)‖2+α2‖u(0)‖2-νE‖u‖2dt+

因为H1嵌入到L2中，有

E‖u‖2≤‖u(0)‖2+α2‖u(0)‖2-νλ1E‖u‖2dt+

(7)

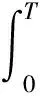
因此，由Gronwall不等式得

(8)

由(7)，(8)式得

(9)

假设P(t,x.A)是u的转移概率测度，并且

对于任意的x∈H,∀ε>0，∀T>0，存在一个半径为R的球，R>0,BR={x∈H;‖x‖≤R}，根据Chebyshev不等式，由(8)，(9)式得

对于固定的M>0,∀ε>0，当R充分大时，有μT(BR)>1-ε.因此 {μT,T>0}是紧的，并且它的极限是方程(1)弱解的一个不变概率测度.