基于灵敏度分析的中低压一体化配电网电压控制策略

王俊逸，吉兴全*，王怀路，杨 迪

(1.山东科技大学 电气与自动化工程学院，山东 青岛 266590；2. 国网山东省电力公司 济宁供电公司，山东 济宁 272000)

传统中低压配电网中的低压信息交换不足、数据采集较少，使中低压配电网难以统一管理.随着配电网中电缆比例的提高，逐步形成电缆与架空线共存的中低压混合配电网，中心配电室和末端配电室已成为配电网的重要控制节点.在此背景下，形成了中低压一体化配电网，即：将低压数据纳入中压配电网，管理中心对中低压配电网进行统一调度和管理.然而，中低压一体化配电网存在以下问题：(1)尚未建立有效的一体化控制模型；(2)分布式电源的接入，使单一的网荷特性变为复杂的网源荷特性.

分布式电源为高效的清洁能源，其接入电网是配电网发展的趋势[1]，但其出力的随机性可造成配电网电压质量的下降[2].除配电网常见的电压越下限外，当分布式电源出力较大、系统负荷较小时，会出现反向潮流，导致部分节点电压越上限.以上情况出现时，仅通过传统控制方式很难保证配电网的电压质量和供电可靠性[3]，这就需要充分利用配电网的可控资源，解决分布式电源并网带来的电压越限问题.传统的电压调控设备主要有：有载调压变压器(on-load tap changer, 简称OLTC)及无功补偿装置.在智能电网环境下，分布于中低压配电网的可控分布式电源、可控负荷及储能等，均可作为控制资源.通过这些资源可实现中低压配电网一体化，使各节点电压不超过允许范围.

在分布式电源控制方面，文献[4]建立了以网损和电压偏移为目标的优化模型，通过调整分布式电源无功出力以及控制无功补偿设备实现优化，并得到了多目标优化的Pareto解集.文献[5]通过控制分布式电源逆变器、OLTC及开关电容器，实现了配电网无功优化.文献[6]提出一种基于光伏系统的无功补偿及有功缩减的电压控制方案.

在灵敏度分析方面，文献[7]提出一种基于灵敏度分析的电压控制策略，建立了在直角坐标系下的电压-无功灵敏度矩阵.文献[8]分析了多种控制策略对节点电压和线路损耗的影响，基于灵敏度提出了一种面向主动配电网的电压-无功控制策略.文献[9]建立了配电网多目标三相不平衡优化控制模型，提出了一种自适应目标权重的控制方式.以上文献均以中压网络为模型，未构建中低压一体化的控制模型.笔者提出中低压一体化的控制策略，建立包含中压和低压多个电压等级的控制模型，解决不同越限情况下的电压和网损问题.

1 灵敏度分析

灵敏度表征系统的输出因变量对自变量变化的敏感程度，主要包括电压灵敏度、网损灵敏度.电压灵敏度表征节点电压对节点注入有功和无功的敏感程度[10]，网损灵敏度表征系统网损对节点注入有功和无功的敏感程度.

1.1 电压灵敏度

在有n个节点的配电系统中，功率平衡方程[11]为

(1)

其中：ΔPi,ΔQi分别为节点i的有功、无功偏移量;Pis,Qis分别为注入节点i的有功功率、无功功率;Pi,Qi分别为节点i的负荷有功功率、无功功率;Gij,Bij分别为节点i,j间的电导、电纳;Vi,Vj分别为节点i,j的电压;δij为电压相角差.

对式(1)进行线性化处理后，得到的方程为

(2)

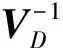
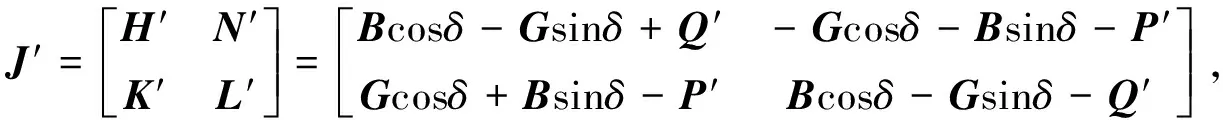
(3)

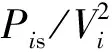
节点电压随有功和无功的变化[12]为

ΔV=[(G+P′)+(B-Q′)(G-P′)-1-(B+Q′)]-1ΔP/V-

[(B-Q′)+(G-P′)(B+Q′)-1(G+P′)]-1ΔQ/V.

(4)

1.2 网损灵敏度

有功网损[13]可表示为

(5)

网损对节点注入有功和无功的灵敏度[13]为

(6)

联合

(7)

及雅克比矩阵J，可求得式(6).

2 电压控制模型

中低压一体化配电网电压控制模型的核心是将低压侧用户归算至中压侧，然后进行统一潮流计算.构建统一的目标函数，考虑中压配电网和低压配电网各类控制单元的约束条件，针对中低压配电网中可能出现的电压越限情况，控制中低压配电网设备，解决电压越限问题，优化整体网损.

2.1 目标函数

电压偏移量表示运行电压偏离额定电压的程度，反映配电网的电压质量，其表达式为

(8)

其中：N为中低压配电网的总节点数，Vn为额定电压，fstep1为第1阶段的目标函数.

系统的网损表达式为

(9)

其中：Ploss,i为第i条线路的有功损耗，b为中低压配电网的支路数，fstep2为第2阶段的目标函数.

2.2 约束条件

约束条件包括等式约束和不等式约束.等式约束为系统潮流约束，由式(1)给出.不等式约束如下：

节点电压约束为

Vimin≤Vi≤Vimax，

(10)

其中：Vimax，Vimin分别表示节点i的电压上、下限.

有载调压变压器的电压挡位约束为

Timin≤Ti≤Timax，

(11)

其中：Timax，Timin分别表示有载调压变压器的电压挡位的上、下限.

并联电容器的无功功率约束为

0≤QCi≤QCimax，

(12)

其中：QCi为节点i处电容器的无功功率，QCimax为电容器的无功功率上限.

光伏输出功率约束为

0≤PDG,i≤PDG,imax，

(13)

其中：PDG,i为i节点的光伏有功功率，PDG,imax为i节点的光伏有功功率上限.

逆变器输出无功功率约束为

(14)

其中：SDG,i为节点i的光伏逆变器的视在功率，QDG,i为节点i的光伏无功功率.

光伏有功功率削减约束为

(15)

储能系统的约束为

0≤PESS,i≤PESS,imax，

(16)

其中：PESS,i为储能系统的功率，PESS,imax为储能系统的功率上限.

除上述配电网运行指标外，为防止配电网节点电压在优化控制后再次越限，需引入惩罚函数以保证配电网节点电压处于正常范围.惩罚函数的表达式为

(17)

由于目标函数和惩罚函数量纲不同，须对各阶段目标函数作归一化处理.笔者分别选取初始网损和电压偏移量作为两阶段目标函数的归一化基准值.考虑惩罚函数后的第1，2阶段的目标函数分别为

Fstep1=fstep1/fB1+fpunish，

(18)

Fstep2=fstep2/fB2+fpunish，

(19)

其中：fB1和fB2为归一化基准值.

2.3 调控量

Vcontrol为电压恢复正常时所需的调控量，其表达式为

(20)

2.4 控制流程

控制流程如图1所示，具体步骤为:(1)将低压侧归算至中压侧进行统一潮流计算后，对中压配电网和低压配电网的节点进行电压越限判断.(2)计算越限节点的调控量，选取调控量最大的节点i作为分析节点.(3)计算控制设备所在节点的有功和无功出力相对于节点i的电压灵敏度，选取电压灵敏度最大的设备为控制设备，利用遗传算法优化电压偏移.电压控制结束后，若电压未恢复至正常状态，则选取电压灵敏度次优的设备为控制设备，继续优化，直至电压水平恢复正常.(4)若电压恢复正常，则计算各控制变量的网损灵敏度，剔除已参与调控的设备，对剩余的控制设备，选取网损灵敏度为负且绝对值最大的设备为网损优化阶段的控制设备，然后优化网损.(5)若初始状态电压不越限，则直接进入网损优化阶段.

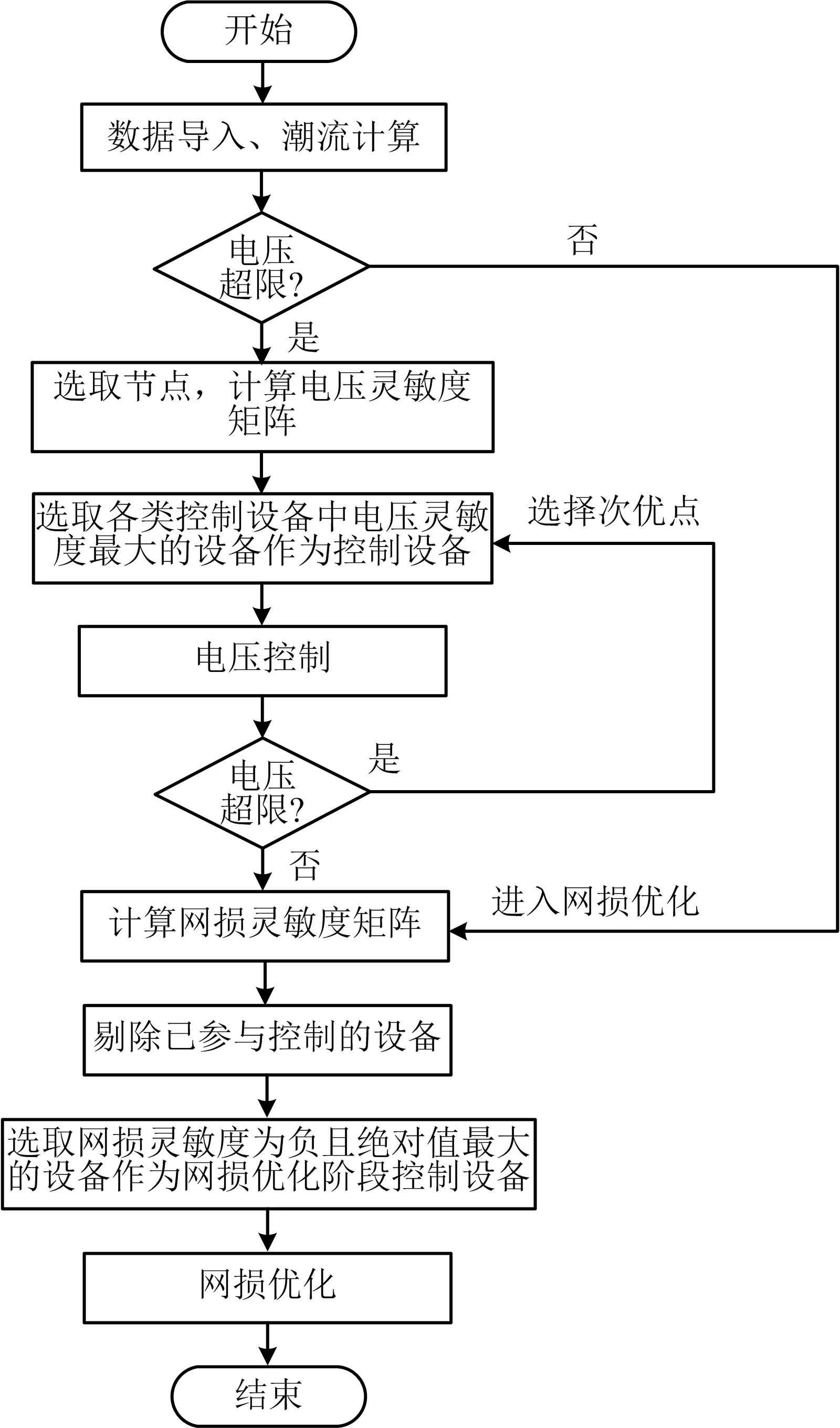
图1 控制流程

3 算例分析

以扩展的IEEE33节点系统为例，验证该文控制策略的有效性.在原系统的基础上，于22节点处连接12.66 kV/0.4 kV的降压变压器，形成中低压一体化配电网.图2中，中压负荷为3 715+j2 290 kVA，低压负荷为375+j229 kVA.在中压区，配电网的11，18，31节点处均安装光伏系统，光伏的最大功率为1 425 kW、额定功率因数为0.95，光伏逆变器的视在功率为1 500 kVA；在光伏并网点，均安装有功功率为1 000 kW的储能设备.在低压区，配电网的36，38，40，43，46，49节点处均安装光伏系统，光伏的最大功率为450 kW、额定功率因数为0.9，光伏逆变器的视在功率为500 kVA；在光伏并网点，均安装有功功率为500 kW的储能设备；在12，15，17，29，32节点处均安装10组电容器，每组电容器的无功功率为20 kVar.

图2 被测试系统

遗传算法的种群数为40，迭代数为60，变异概率为0.1，交叉概率为0.8.

3.1 电压越下限

当系统负荷较高，且光伏出力不足时，长线路末端易出现节点电压越下限.假定所有光伏单元的有功出力为0，中压区储能设备初始功率为100 kW，低压区储能设备初始功率为50 kW,储能节点可向系统输出有功功率.经初始潮流计算得到的电压越下限时的节点电压如图3所示.

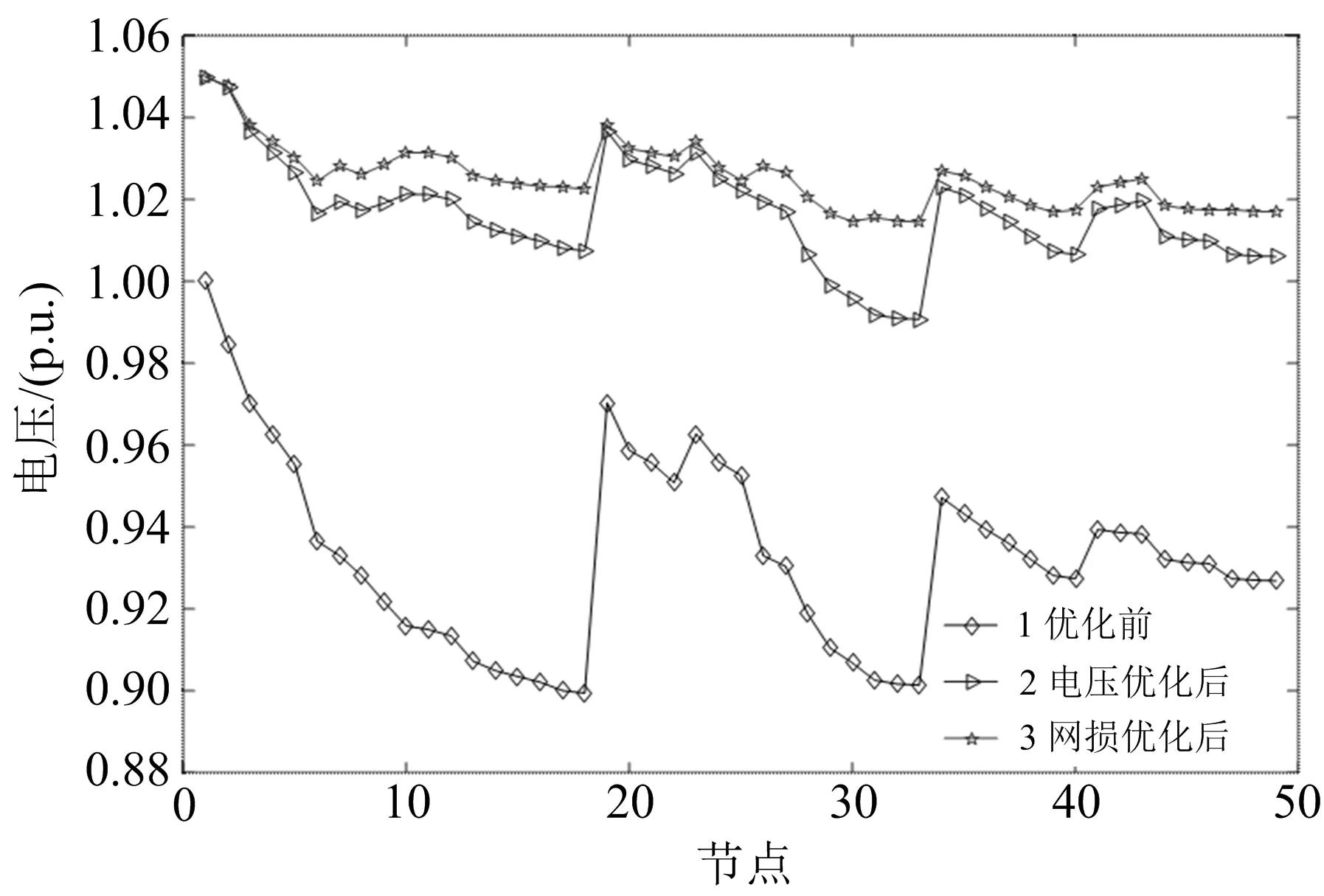
图3 电压越下限时的节点电压

由图3中优化前的节点电压可知，中压和低压区域有大量节点越下限，其中中压配电网末端18节点和低压配电网末端49节点电压越限较严重.先进行电压优化，后进行网损优化.由图3中电压优化后的节点电压可知，调控节点电压恢复至正常后，其余节点电压均恢复至正常水平；有载调压变压器电压挡位调节至+5%时，电压偏移量由3.287 5 p.u.下降至1.641 4 p.u..由图3中网损优化后节点电压可知，在有载调压变压器电压挡位保持不变情况下，网损优化后各节点电压均有所提高，电压波动性明显下降，电压偏移量由1.641 4 p.u.下降至1.207 5 p.u..可见，两种优化后，节点电压均能恢复至正常水平.

初始潮流计算后，电压越下限时的中低压配电网的系统网损为290 kW.电压优化后系统网损下降至207 kW，这是由于此时电压控制设备的网损灵敏度为负值，有功和无功的注入使系统网损降低.网损优化后系统的网损由207 kW下降至199 kW.可见，两种优化后，网损有明显下降.

3.2 电压越上限

当系统的光伏出力较大或者无功补偿较高且负荷使用率较低时，配电网产生反向潮流使节点电压越上限.当电压越上限时，希望通过储能设备吸收部分光伏的功率，从而降低注入系统的功率，然后利用光伏逆变器吸收无功功率以降低节点电压.初始状态下有载调压变压器电压挡位为+2.5%，中压配电网光伏有功出力为1 350 kW，低压配电网光伏有功出力为320 kW，功率因数为0.95.各节点均接入两组电容器.

经初始潮流计算得到的电压越上限时的节点电压如图4所示.

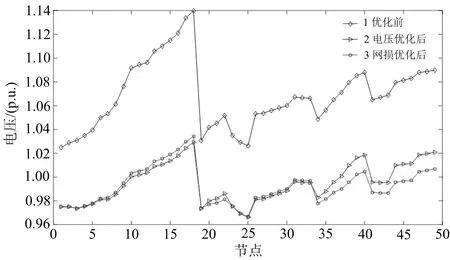
图4 电压越上限时的节点电压

由图4中优化前的节点电压可知，中压配电网有大量节点电压越上限，最严重的是末端18节点.而低压配电网也有大量节点电压超上限，末端49节点电压越限最严重.先进行电压优化，后进行网损优化.由图4中电压优化后的节点电压可知，调控节点电压恢复至正常范围后，其余节点电压均恢复至正常水平.有载调压变压器电压档位调至-2.5%时，电压偏移量由 2.127 9 p.u.下降至1.016 1 p.u..由图4中网损优化后节点电压可知，在有载调压变压器电压档位保持不变的情况下，中压配电网各节点电压均有所提高，低压配电网各节点电压均明显下降.

初始潮流计算后，电压越上限时的中低压配电网的网损为241 kW.经电压优化后网损下降至164 kW.网损优化后网损由164 kW下降至135 kW.与初始状态比较，两种优化后的网损有明显降低.

3.3 算法对比

笔者提出的控制策略由灵敏度指导算法实现.基于配电网多目标函数控制策略，通常以权重的形式将多目标函数转化为单目标函数，该控制策略由多目标优化算法实现.通过比较多目标优化算法与灵敏度指导算法的优化结果，验证笔者所提控制策略的有效性.以电压越下限为例，两种算法优化结果对比如图5所示.

图5 两种算法优化结果对比

由图5可知，两种算法均能使节点电压恢复至正常范围内，而多目标优化算法优化后的电压水平明显低于灵敏度指导算法且波动较大.

多目标优化算法优化后网损为203 kW，电压偏移量为1.469 7 p.u.，而灵敏度指导算法优化后网损下降为199 kW，电压偏移量下降为1.207 5 p.u..这是由于权重的选择不能使两目标函数同时最优，而灵敏度指导算法通过灵敏度将多目标优化转化为两单目标优化，能实现两目标函数的最优.在优化速度上，多目标优化算法的计算时间为381 s，而灵敏度指导算法的计算时间为307 s.由于灵敏度指导算法单次控制的变量少，因此在寻找最优解的过程中其速度要明显快于多目标优化算法.

4 结束语

笔者提出了一种基于灵敏度分析的中低压一体化配电网电压控制策略，通过控制设备间的协调，有效解决了电压越限问题，使节点电压恢复至正常水平，同时降低了节点电压偏移量，限制了电压波动，减少了系统网损.通过灵敏度将多目标优化转换为两单目标优化，可减少单次优化的控制设备数，提高了优化速度，解决了多目标优化中目标函数权重难以平衡的问题.算法对比结果表明，灵敏度指导算法寻优速度快于多目标优化算法.