基于理性预期均衡框架下的价格泡沫与过度反应研究
张 强,曹 阳,曾庆铎,刘善存
(1.北京化工大学经济管理学院,北京 100029;2.北京航空航天大学经济管理学院,北京 100191)
1 引言
Kindleberger[1]将泡沫定义为价格在一段时间内突然连续上涨并超出人们的预期。Rosser[2]认为泡沫是由非随机冲击造成的价格偏离基础价值的现象。Garber[3]则指出这种现象无法通过股票的基本面进行解释。价格泡沫在世界范围内普遍存在,荷兰郁金香泡沫、法国密西西比泡沫以及英国南海泡沫等都是价格泡沫出现的典型案例[4]。当市场存在泡沫时,价格发现功能的缺失会导致投资者无法通过价格获取关于风险资产价值的信息,从而做出错误的投资决策,扰乱资金流向,破坏资本市场有效配置资金的功能。由于价格泡沫对资源配置效率和股票市场的稳定性有着重要影响,因此备受学者关注。
传统的金融理论以有效市场假说为基础,结合交易量、历史收益等因素解释价格变化。Blanchard[5]证明在理性投资者参与的市场中,股票价格方程的解仍包含泡沫成分。Chen等[6]构建了回归模型,发现价格泡沫可能与前六个月的交易量增加有关。周春生和杨云红[7]则认为价格泡沫是市场制度不完善造成的结果。但由于有效市场假说本身的局限性,一些泡沫现象不能得到令人满意的解释。投资者有限理性和金融异象的出现也促使一些学者另辟蹊径,利用行为金融学理论分析价格泡沫。
行为金融学理论表明投资者的决策与传统的金融理论之间存在系统性偏差,投资者作为股票市场的参与者,其行为对市场均衡有着显著的影响。Lux[8]认为羊群效应可能导致股票市场出现泡沫。Deniel等[9]以及Scheinkman和Xiong[10]也通过投资者的心理偏差描述了泡沫的形成过程且实证结果显著。因此越来越多的人开始利用非理性因素研究价格泡沫,而过度反应作为实验心理学一个重要的非理性因素也成为实验经济学研究的热点。
过度反应是指有限理性的投资者对某一信息或事件做出了比正常情况下更加剧烈的反应,他们倾向于重视眼前的信息而轻视以往的信息。De Bondt和Thaler[11]最早研究了股票市场中的过度反应现象,他们以1926到1982年间在NYSE 上市的股票为对象,通过比较投资组合的收益证明了过度反应的存 在。Tripathi和Aggarwal[12]、Boussaidi[13]以及Foss和Warholm[14]对印度、突尼斯和挪威股票市场的分析不仅证实了过度反应的存在,还进一步发现过度反应会使股票价格发生超出预期的剧烈波动。陈国进和范长平[15]以及杨胜刚和成博[16]在我国的股票市场中得到了类似的结论。
目前基于过度反应的股票市场价格泡沫研究大多停留在实证方面,鲜有文章从微观结构的角度分析两者之间的内在联系。BSV[17]和DHS[18]模型分别利用选择性偏差和归因偏差解释了过度反应如何导致价格偏离有效市场假说。HS[19]模型假设市场中存在两类投资者,消息观察者基于信息进行交易,而动量交易者的决策完全依赖于价格,并将过度反应归结于信息逐渐扩散的结果。De Long等[20]提出了带噪声交易的理性预期均衡模型,从噪声交易者的非理性行为入手讨论了股票价格与基础价值偏离的现象。王连华和杨春鹏[21]扩展了DSSW 模型,指出过度反应会引起价格泡沫,但他们均未考虑知情交易者存在过度反应的可能性。
陈耀年和周学农[22]认为投资者普遍存在过度反应。Vives[23]则指出噪声交易者的行为仅仅是为了满足其流动性需求,而知情交易者的策略才对资产定价起到了主导作用。本文以此建立了一个两期的理性预期均衡模型,着重研究知情交易者存在过度反应对资产定价及均衡特征的影响,并对其逻辑机理进行解析。在第1期时,先期知情交易者会收到一个私人信息,后期知情交易者则没有这个信息。在第2期时,先期知情交易者和后期知情交易者都会收到一个公共信息。此时公共信息的出现对股票市场的影响并不容易判断,Kahneman 和Tversky[24]认为,投资者对新信息的认知常常违反Bayes规则,他们会高估最近的信息并给予更大的权重,这可以理解为投资者对新信息过度反应。模型假设投资者在获取信息的同时也观察市场价格,他们据此提交需求计划。出清价格受所有投资者决策的影响的同时也改变了他们的信息集,进而影响其交易策略,一个自我加强过程由此形成。这为利用过度反应解释价格泡沫的成因提供了新的思路。
在价格泡沫的衡量方面,不同于Shiller的有界方差检验、Engle和Granger的协整检验以及West的Euler方程检验等数理统计方法[25],我们从基本面入手,采纳Peress[26]的观点利用1/Var[v|p]来衡量价格信息量。当价格信息量足够大时,价格充分反映了市场中的信息,市场效率越高。反之价格偏离价值,股票市场存在泡沫。Sadka和Scherbina[27]指出价格泡沫通常伴随着流动性的变化,因此本文也对其进行了讨论。通过以上研究发现,在私人信息外生获取的情况下,知情交易者过度反应程度的增加会提高第2期的价格信息量,对第1期则没有影响。在私人信息内生获取的情况下,挤出效应的存在减少了先期知情交易者的比例,因此降低了第1期的价格信息量,从而形成价格泡沫。此时流动性则可能呈先降低后提高的U型变化。当新信息到达后,第2期的价格信息量有所提高,但相比于私人信息外生获取的情况仍存在差距。
2 模型
考虑一个两资产的模型,其中包括有风险的股票和无风险的债券。假设股票的价格为p,基础价值为v,v~N(¯v,τ-1v),¯v>0,τv>0。无风险债券的利率标准化为0。市场的参与者包括噪声交易者和在[0,1]内均匀分布的知情交易者。知情交易者又可以分为先期知情交易者和后期知情交易者,μ为先期知情交易者的比例。
将模型的投资期限设置为两期,投资者在每期期初进行资产的选择,在期末进行清算[28]。在第1期时,先期知情交易者i会收到一个私人信息s i=v,且满足即所有先期知情交易者私人信息加总后的平均值收敛于股票的基础价值。先期知情交易者也可以通过观察市场价格p1获取信息,后期知情交易者没有私人信息,仅可以观察市场价格p1。噪声交易者没有任何信息,为市场提供了流动性。此时,先期知情交易者i的信息集为I i1={si,p1},后期知情交易者u的信息集为Iu1={p1}。在第2期时,市场披露一个公共信息,先期知情交易者i和后期知情交易者u都可以收到这个新信息s′i和s′u,其中s′i=v+ε′i,李诗林和李扬[29]对沪深股票市场进行了实证研究,发现投资者会对新信息过度反应。也就是说虽然新信息的精度仍为τε,但由于知情交易者对其过度反应并给予了更大的权重,因此我们假设他们对新信息的精度认 知 为rτε,r表 示 过 度 反 应 程 度,r>1,r越大,新信息权重越大。类似于第1期,先期知情交易者和后期知情交易者仍可以通过观察市场价格p2获取信息,噪声交易者没有任何信息。此时,先期知情交易者i的信息集为I i2= {si,s′i,p1,p2},后期知情交易者u的信息集为I u2= {s′u,p1,p2}。这与彭叠峰等[30]对投资者类型的划分类似,本文的先期知情交易者可对应于关注交易者,而后期知情交易者则可对应于疏忽交易者。
假设投资者具有CARA 型效用函数U(π),我们将风险厌恶系数标准化为1,因此U(π)=-exp(-π),其中π=(v-p)x为投资者的利润,x为其对股票的需求量。投资者的决策就是要基于其信息集I来最大化条件期望效用函数,即Max E[-exp(-π)|I]。根据CARA 效用函数的定义,当信息集为I时,最大化上述期望效用函数等价于求解Max(E[π|I]-(1/2)Var[π|I])。代入π,我们可以得到一个关于需求量x的二次函数,因此可以解出需求量此时期望效用达到最大,为同时我们假设噪声交易者在第t期的流动性需求为x t,x t~N(0,),τx>0,且有v、εi、ε′i、ε′u和x t相互独立。噪声交易者不仅非知情而且非理性,他们没有需求函数。当x t>0时,噪声交易者提交买单,反之则提交卖单并为市场提供随机供给。
3 金融市场均衡
3.1 第1期的金融市场均衡
首先给出金融市场均衡的定义。
定义1(金融市场均衡)第t(t=1,2)期的金融市场均衡需要满足:
(1)效用最大化条件:
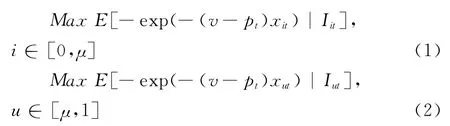
(2)市场出清条件:
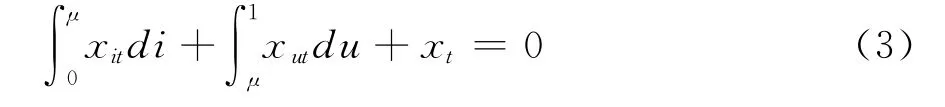
在第1期时,知情交易者提交需求计划,相当于限价订单。假设先期知情交易者的交易策略x i1(si,p1)=ai1si-bi1p1+d i1,后期知情交易者的交易策略x u1(p1)=-bu1p1+d u1,其中ai1、bi1和bu1分别代表不同投资者对私人信息和市场价格的敏感程度。把x i1和x u1分别代入市场出清条件可以得到第1期的价格函数表达式
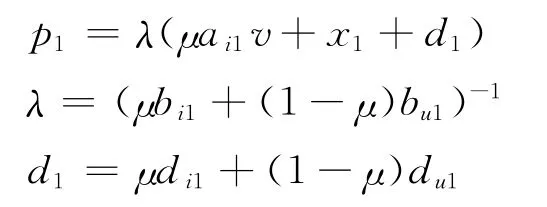
接下来我们分别计算先期知情交易者和后期知情交易者效用最大化时的需求量。
对于先期知情交易者i,其需求x i1=利 用Vives[23]的方法,我们可以得到

同理对于后期知情交易者u,其需求
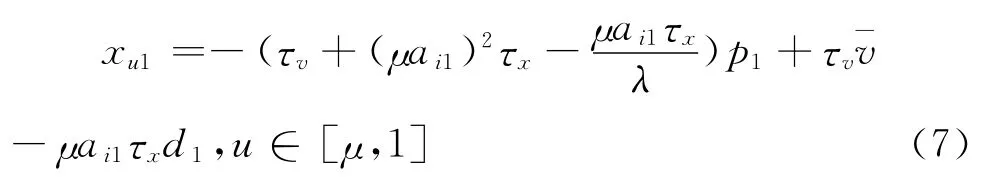
把x i1和x u1分别与先期知情交易者和后期知情交易者的交易策略对比系数,可以解出ai1、bi1、d i1、bu1、d u1、λ和d1。由此可得定理1。
定理1在第1期的金融市场中存在唯一的线性理性预期均衡,先期知情交易者i的交易策略x i1(si,p1)=ai1si-bi1p1+d i1,后期知情交易者u的交易策略x u1(p1)=-bu1p1+d u1,均衡价格p1=λ(μa i1v+x1+d1),其中

定理1反映了第1期的金融市场均衡,此时投资者的交易策略仅与私人信息、市场价格以及噪声交易者的需求相关,先期知情交易者比例越高,私人信息精度越精确,均衡价格受噪声影响也就越小,股票价格更能反映基础价值。
为了便于理解投资者的交易策略,我们将其需求函数分别表示为

首先考虑后期知情交易者,由于bu1=τv+当价格高于基础价值时,他们会卖出股票,当价格低于基础价值时,他们会买入股票。即后期知情交易者始终逆潮流而动,这可以看作一种典型的做市商行为。此时后期知情交易者面临一个逆向选择问题,因为他们不知道交易对手是先期知情交易者还是噪声交易者,其交易强度bu1随先期知情交易者比例μ的增加而降低。先期知情交易者的情况较为复杂,其有两个原因参与交易。第一,他们利用私人信息进行投机,当价格大于私人信息时买入股票,当价格小于私人信息时卖出股票,其交易强度ai1由私人信息精度τε决定,与噪声交易无关。第二,类似于后期知情交易者,先期知情交易者的交易策略中也包含做市部分。
3.2 第2期的金融市场均衡
在第2期时,假设先期知情交易者i的交易策略后期知情交易者u的交易策略x u2(s′u,p1,p2)=au2s′u-bu2p1-cu2p2+d u2,其中ai2、au2、bi2、bu2、ci2和cu2分别代表不同投资者对私人信息、公共信息以及两期市场价格的敏感程度。把x i2和x u2分别代入市场出清条件可以得到第2期的价格函数表达式
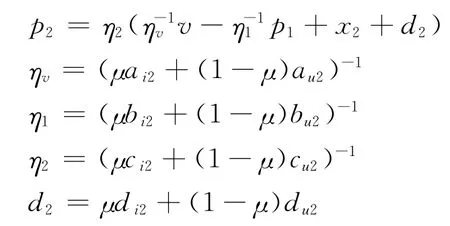
接下来我们分别计算先期知情交易者和后期知情交易者效用最大化时的需求量。
对于先期知情交易者i,其需求x i2=。类似于第1期,我们可以得到

同理对于后期知情交易者u,其需求

把x i2和x u2分别与先期知情交易者和后期知情交易者的交易策略对比系数,可以解出ai2、bi2、ci2、d i2、au2、bu2、cu2、d u2、ηv、η1、η2和d2。由此可得定理2。
定理2在第2期的金融市场中存在唯一的线性理性预期均衡,先期知情交易者i的交易策略后期知情交易 者u的 交 易 策 略x u2(s′u,p1,p2)=a u2s′u-bu2p1-cu2p2+d u2,均衡价格+x2+d2),其中
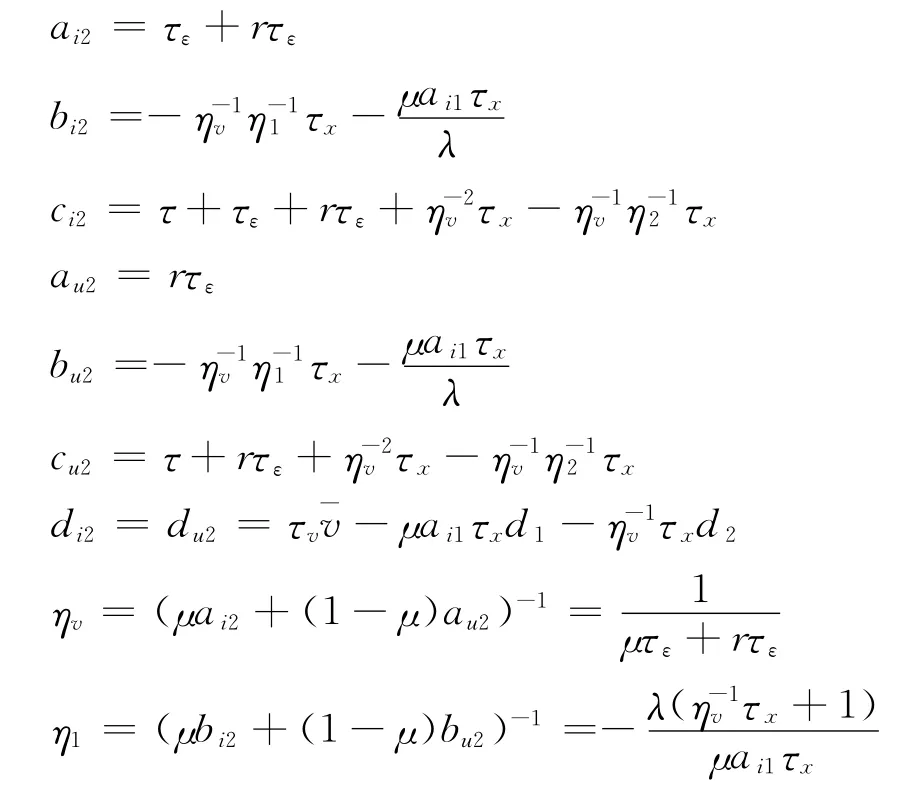

定理2反映了第2期的金融市场均衡,此时投资者的交易策略和均衡价格不仅与私人信息、公共信息、两期市场价格以及噪声交易者的需求相关,还受到过度反应因素的影响。类似于第1期,我们仍可将投资者的需求分解为投机和做市两部分,此时由于市场披露一个公共信息s′u,先期知情交易者和后期知情交易者还会对该公共信息进行投机,这里不再赘述。
但王鸿儒[32]、杜 欣 依[33]和 郁 晨[34]等 实 证 研 究表明投资者过度反应程度的增加并不会提高市场效率,反而会降低价格信息量,形成价格泡沫。这并不符合之前的结论,其主要原因是外生了先期知情交易者的比例,接下来我们将从信息市场均衡的角度对这一现象进行解释。
4 信息市场均衡
4.1 内生信息获取
不同于金融市场均衡中私人信息外生获取的情况,我们假设一个投资者需要付出成本c才能获取到私人信息成为先期知情交易者。记均衡时先期知情交易者的比例为μ*,μ*可以通过比较先期知情交易者与后期知情交易者的期望效用来决定。利用Grossman和Stiglitz[35]的方法,我们可以计算先期知情交易者i在第1期时的效用

同理,先期知情交易者i在第2期时的效用

后期知情交易者u在第1期时的效用

后期知情交易者u在第2期时的效用

上述效用的确定性等价形式为
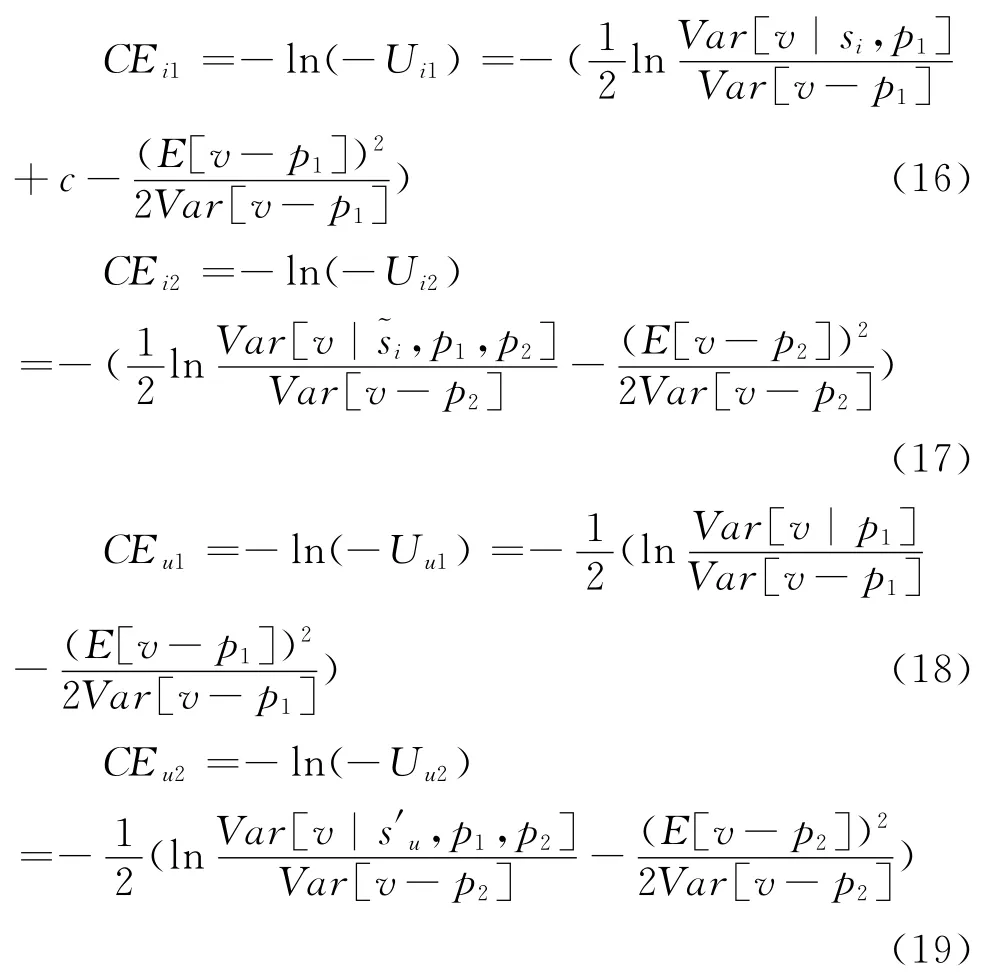
因此先期知情交易者i的确定性等价效用可以表示为CE i=CE i1+CE i2,后期知情交易者u的确定性等价效用可以表示为CE u=CE u1+CE u2。私人信息获取成本不仅影响了先期知情交易者的比例和第1期的均衡价格,还通过价格信息量影响了知情交易者在第2期时的效用。我们假设私人信息的净收益为B,


与ηv的区别仅在于将μ替换为μ*。
下面给出信息市场均衡的定义。
定义2(信息市场均衡)
(1)如果B<0,则μ*=0;
(2)如果B>0,则μ*=1;
(3)如果B=0,则0<μ*<1。
如果私人信息的净收益为负,那么没有人愿意成为先期知情交易者,则μ*=0 是一个均衡;如果私人信息的净收益为正,那么所有人都愿意成为先期知情交易者,则μ*=1是一个均衡;如果私人信息的净收益为0,也就是说成为先期知情交易者与不成为先期知情交易者在期望效用上并无差异,则存在μ*,使得0<μ*<1是一个均衡。由于B是μ*的减函数,故均衡是唯一的。
当B=0时,我们有

私人信息的净收益B是知情交易者过度反应程度r的减函数,当B增加时,更多人愿意成为先期知情交易者,反之则减少了先期知情交易者的比例μ*,即μ*与r呈负相关关系,由此可得定理3。
定理3(挤出效应)假设0<μ*<1,知情交易者过度反应程度的增加挤出了私人信息的生产,即dμ*/dr<0。
我们对定理3 进行数值模拟,类似于Han 和Yang[36],不失一般性,给定参数取值τv=τε=τx=1,c=0.3,结果如图1所示。
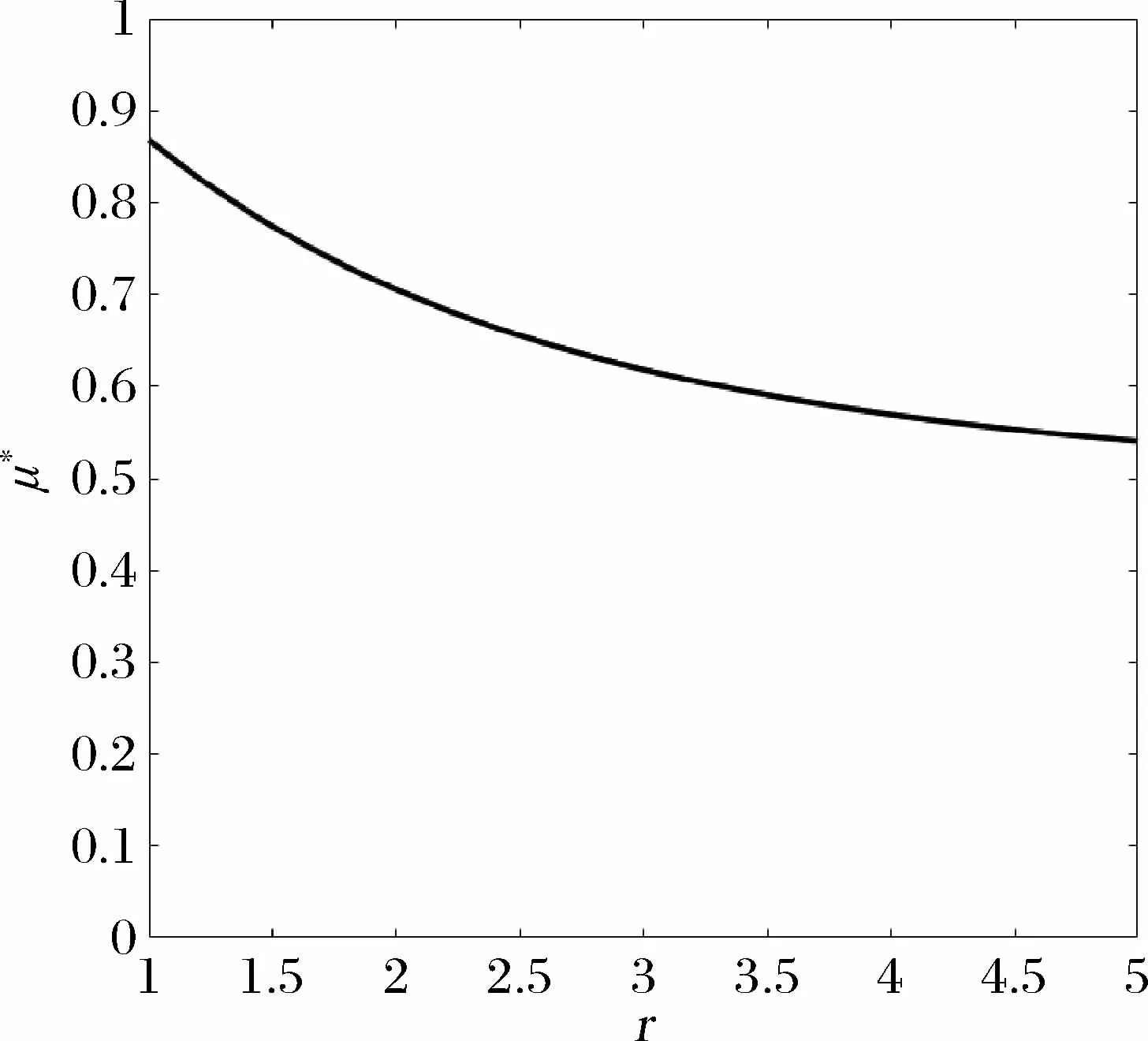
图1 过度反应程度与先期知情交易者比例关系图
私人信息之所以被挤出是因为知情交易者在第1期时预期新信息即将到达并对其过度反应,通过比较净收益B的变化决定是否付出成本成为先期知情交易者。知情交易者过度反应程度的增加对μ*有一个直接影响和一个间接影响。直接影响是随着r的增加,新信息权重也随之增加,私人信息权重则相对减少,这就减弱了投资者购买私人信息的意愿。间接影响是新信息权重的增加降低了噪声的不确定性,提高了价格的信息含量,投资者可以从价格中获取更多信息,这就加强了他们“搭便车”的动机。
接下来我们将在满足信息市场均衡的条件下研究知情交易者过度反应程度对股票市场的影响。
4.2 均衡分析
在价格信息量方面,当r增加时,为了使B=0成立,因此增加。又因为=的增加提高了价格的信息含量。由于挤出效应的存在,融入价格中的私人信息相对减少,但知情交易者过度反应程度的增加也降低了噪声的不确定性,对的总体影响仍是积极的。我们将此时的价格信息量与私人信息外生获取的情况进行比较,发现虽然知情交易者过度反应程度的增加提高了价格信息量,但μ*的减少在一定程度上抑制了()-1的增加。也就是说在私人信息内生获取的情况下,第2期的价格信息量相对于私人信息外生获取时存在差距,并且这种差距会随着r的增加进一步扩大。
需要注意的是,在私人信息内生获取的情况下,新信息对股票市场的影响不仅体现在第2期,挤出效应的存在减少了先期知情交易者的比例,导致第1期的价格信息量在新信息到达之前就开始变化。
第1期的价格信息量=τv+(μ*ai1)2τx,r的增加挤出了μ*,先期知情交易者比例的减少直接降低了,即知情交易者过度反应程度的增加对价格信息量有着消极影响,价格泡沫由此形成。
同时我们考虑价格泡沫出现时流动性的变化[36]。第1期的流动性
L1= (λ*)-1=的减少对L1有两个相反的影响。可以证明∂L1/∂μ*>0当且仅当此时私人信息缺失的影响大于逆向选择风险降低的影响,因此降低了流动性。反之μ*<此时私人信息缺失的影响小于逆向选择风险降低的影响,因此提高了流动性。也就是说L1可能随r的增加先降低后提高,呈U型变化,由此可得定理4。
定理4在私人信息内生获取的情况下,知情交易者过度反应程度的增加提高了第2期的价格信息量。但挤出效应的存在减少了先期知情交易者的比例,因此降低了第1期的价格信息量,从而形成价格泡沫,第1期的流动性则可能呈先降低后提高的U型变化。

图2 先期知情交易者比例与流动性关系图
因为μ*是r的减函数,图2展示了μ*减少时流动性L1的变化,此时参数取值为τv=τε=1,τx=3。
综上所述,由于知情交易者获取私人信息需要付出成本,其理性预期行为促成了第1期市场均衡特征的改变。他们预期新信息即将到达并对其过度反应,通过挤出效应减少了先期知情交易者的比例,导致价格信息量也随之降低,从而形成价格泡沫。当新信息到达后,价格信息量有所提高,但相比于私人信息外生获取的情况仍存在差距。价格泡沫可以通过两种途径进行改善:第一,加强信息披露,降低私人信息获取成本,净收益的增加使得更多人愿意成为先期知情交易者。第二,弱化投资者的过度反应程度,当知情交易者过度反应程度较低时,私人信息生产被挤出的部分也相对较少,对价格信息量的提高起到一定促进作用。
5 结语
本文假设知情交易者存在过度反应,当新信息到达时,他们会对其过度反应并给予更大的权重。通过建立一个两期的理性预期均衡模型,将信息延迟现象引入市场。针对交易者对先、后获取的信息反应程度引入过度反应。通过比较前后两期价格信息量的变化,讨论了知情交易者过度反应程度与价格泡沫之间的关系,具体结论如下:
在私人信息外生获取的情况下,知情交易者过度反应程度的增加会提高第2期的价格信息量,对第1期则没有影响。在私人信息内生获取的情况下,挤出效应的存在减少了先期知情交易者的比例,因此降低了第1期的价格信息量,从而形成价格泡沫。此时流动性则可能呈先降低后提高的U型变化。当新信息到达后,第2期的价格信息量有所提高,但相比于私人信息外生获取的情况仍存在差距。价格信息量的降低意味着价格不能较好地反映价值,即价格与价值之间出现较大偏差,这并不利于资源配置效率的提高,对股票市场的稳定性也产生了消极影响。
我国股票市场成立时间相对较晚,却在短短的二十余年间经历了数次大起大落,泡沫化趋势明显。在实际中,价格泡沫的成因可能更加复杂,不同投资者的过度反应程度也不尽相同,但本模型仍可为投资者和管理层提供了一点参考。投资者应该更理性地进行决策,管理层也应该通过降低私人信息获取成本等手段加强信息披露,同时完善入市教育,弱化投资者的过度反应程度,使股票市场走上健康发展的道路。

