基于政府隐性担保退出预期的金融机构违约风险重定价

冯 玲，文 璐，肖 阳

（福州大学经济与管理学院，福建 福州 350000）

1 引言

长期以来，在我国金融领域普遍存在着政府隐性担保问题，尤其是在金融机构的市场退出体制上［1］。在政策扶持和政府担保下即便是管理极为不善、技术性破产的金融机构也能够继续经营下去［2］。这使得政府为金融机构提供隐性担保的预期普遍存在于市场中，致使金融市场丧失了风险定价能力，导致资金过度配置到风险高、收益低的经济领域和金融机构，推高了整体经济运行的风险水平。为防范风险过度累积，中国政府推出了存款保险制度，将部分政府隐性担保显性化，同时又于2018 年颁布了《关于规范金融机构资产管理业务的指导意见》（下文简称资管新规）明确提出打破刚兑，结合正在不断完善中的利率市场化改革，政府取消对金融机构的隐性担保，使不具有生存能力的金融机构及时退出，或将成为未来政策重点。

政府政策的改变将会引起市场对于隐性担保预期的改变，进而引发金融机构违约风险的重定价［3］。如果不能准确估计这一过程中金融机构违约风险的变化，那么很有可能会导致市场信心受损，引起投资者挤兑进而增加系统性风险。这使得研究政府隐性担保退出过程中金融机构违约风险的重定价变得尤为重要。

通过梳理国内外学者的研究，发现与本文主题相关的文献主要包括两类，一类是关于政府隐性担保的研究，一类是关于违约风险度量的研究。关于政府隐性担保的文献大都侧重于分析政府隐性担保存在的影响。从政府隐性担保存在性证明［4-5］到政府隐性担保对债务融资成本［6-9］、金融市场纪律［10］的影响再到政府隐性担保的价值测度［11-13］，学者们从各个方面分析了政府隐性担保存在对于金融市场的影响，而对于政府隐性担保退出的研究却较少，仅有的研究又多以存款保险制度的推出为例分析政府隐性担保从隐性转变为显性对于金融市场信心［14］及金融危机发生概率［15］的影响，对于估计政府隐性担保价值转变过程金融机构违约风险的研究较为少见。另一方面，关于信用风险定价的研究较为主流的模型为结构化模型［16-17］，但该模型并未考虑政府隐性担保因素，不能将其直接用于政府隐性担保退出过程中金融机构违约风险的定价。

鉴于此，结合党的十九大报告中提出的“健全金融监管体系，守住不发生系统性金融风险的底线”，本文拓展已有的信用风险结构化模型［17］，将政府隐性担保预期纳入该模型，刻画了政府隐性担保下金融机构资产价值的动态运动规律，重新构建了其违约风险模型，评估了政府隐性担保逐步取消过程中不同风险状态金融机构违约风险的动态演变过程，以期为防范政府隐性担保退出过程中可能增加的系统性风险提供一定的参照意义。与已有的研究相比，本文的边际贡献在于：第一，将政府隐性担保预期纳入信用风险结构模型，建立了包含担保预期的违约风险测度模型，能够为研究金融机构违约风险的动态变化提供一个新的研究思路；第二，估计了政府隐性担保退出过程中不同风险状态金融机构的违约风险，有助于监管当局审慎设置隐性担保改革次序。

2 考虑政府隐性担保预期的金融机构违约风险模型

2.1 金融机构中的政府隐性担保预期描述

在传统的信用风险结构化模型中，通常假设企业的违约行动是由其自身资产价值的随机运动驱动的，当企业自身资产价值低于其债务价值时违约发生。然而，考虑到金融机构破产所带来的巨大社会成本，对于资不抵债的金融机构政府通常不会即刻对之进行法定的破产清算，而是选择在一定的监管宽容度下通过资金注入等对其进行救助，唯有其资不抵债的程度超过了政府可容忍的监管宽容水平时，政府才会对其执行破产清算程序，并在其监管宽容度内代为清偿其清算资产不足以偿付的债务。这种救助与债务偿付行为使得公众普遍认为政府将为问题金融机构兜底而不会放任其倒闭，从而形成了隐性担保预期。基于此，本文将政府隐性担保定义为政府对问题金融机构的直接救助行为及违约时的债务承担行为。借鉴Ronn和Verma［21］的做法，本文将政府隐性担保模型化为如下形式：当金融机构自身资产价值A t低于其债务价值B、但大于政府可容忍的债务上限水平ρB时，即ρB≤A t＜B时，政府将通过注入资金等方式保证其资产价值等于B从而避免其违约；当金融机构自身资产价值低于政府可容忍的债务上限水平时，即At＜ρB时，政府才会宣布金融机构违约并承担（1-ρ）B的损失。这里0≤ρ≤1反映了市场对政府隐性担保程度的预期，可根据政府处置问题金融机构的历史信息及相关政策估计得到。当ρ=0时表示存在完全隐性担保，此时金融机构的违约可能性几乎为0；ρ值越大表明政府隐性担保程度越低；当ρ=1时表示完全不存在政府隐性担保，金融机构资不抵债时，违约即发生，且损失完全由金融机构债权人承担。

2.2 考虑政府隐性担保预期的金融机构违约风险模型构建

2.2.1 离散时间隐性担保情形

首先考虑一种特殊情形：政府隐性担保可能发生在金融机构债务存续期内的固定时刻。为简化分析，假设该固定时刻为和t2=T时刻，其中T表示金融机构债务到期日。即仅在t1和t2时刻，若金融机构自身资产价值低于其债务价值时，政府可能会对其进行救助。

借鉴信用风险结构化模型的普遍做法，假定金融机构自身资产价值服从以下随机运动：

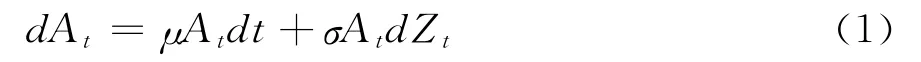
其中A t表示t时刻金融机构资产价值且0≤t≤T，μ表示金融机构资产收益率，σ代表资产收益率的瞬时标准差代表标准高斯维纳过程。那么t1时政府隐性担保发生前金融机构资产价值的瞬时值为：

可能大于B，可能处于ρB和B之间，也有可能小于ρB。若ρB≤＜B那么政府将通过注资等方式为金融机构提供担保，并使得担保后资产价值等于B，即=B，而后A将以B为初始值按照（1）所描述的过程继续运动，直到t2。由式（2）可知，政府在t1时刻直接救助金融机构的概率为：

相应的救助成本为B-；若＜ρB政府将宣布金融机构违约，根据公式（2）可知金融机构在t1时刻的违约概率为：

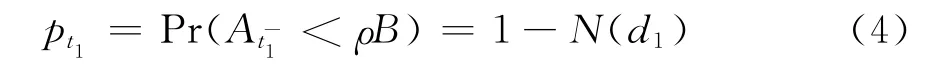
违约时的总预期损失现值为：

其中r表示贴现率。政府将承担的预期损失部分为：

债权人将承担的预期损失为：

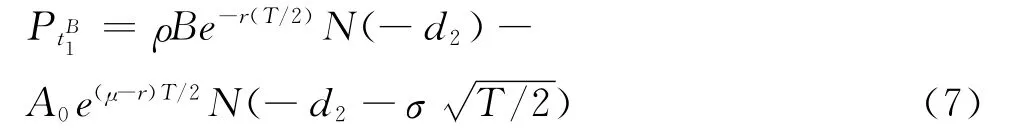
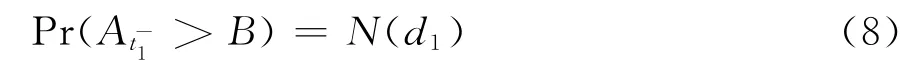
在这种情形下，金融机构可以存活到t2时刻的概率为N（d2）。设t2时刻政府隐性担保发生前金融机构资产价值的瞬时值为，那么将有N（d2）-N（d1）的概率为：

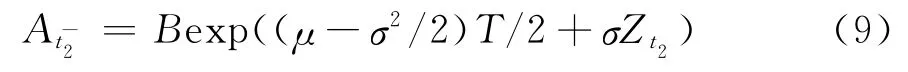
有N（d1）的概率为：

此时，金融机构的违约概率为：

相应的总预期损失现值为：

其中政府将承担的预期损失为：

债权人将承担的预期损失为：

2.2.2 连续时间隐性担保情形

基于2.2.1的分析，扩展离散时间隐性担保情形的假设，考虑更为一般的情形：在金融机构债务存续期内的任意时刻，当A t＜B时债权人都有权要求债务人进行破产清算，并由政府决定此时是否对其进行救助。也就是说，政府隐性担保可能发生在金融机构债务存续期内的任意时刻。

离散时间隐性担保的情形分析说明，当政府通过资金注入等方式直接救助金融机构时，金融机构自身资产价值将在资金注入后发生向上跳跃。这意味着当存在政府隐性担保时，金融机构总资产价值将等于其自身的资产价值与政府直接救助成本之和。用表示考虑政府隐性担保预期的金融机构总资产价值，则：

其中初始资产价值A0满足边界条件：A0＞B。上式中的Gt是一个适应的右连续纯跳过程，满足G0=0，表示t时刻政府直接救助行为发生后资产价值向上跳跃的部分，其跳跃时间与跳跃幅度均依赖于t期之前各时期资产价值运动过程：对于（0，T］内任意时刻t，若ρB≤＜B，政府将进行救助，金融机构资产价值将向上跳跃B-使得=B，反之=。用N（t）表示直到t时刻资产价值向上跳跃的总次数，用θi∈（0，t］（i=1，2，…，N（t））表示第i次跳跃发生的时间，则：

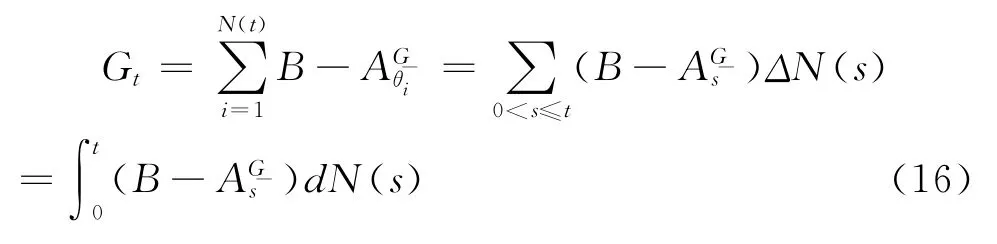
其中θi=inf（0＜s≤t：ρB≤＜B）表示跳跃时间为资产价值处于［ρB，B）区间内的时刻；ΔN（t）=N（t）-N（t-），若t为跳时刻，则ΔN（t）=1，反之ΔN（t）=0。将公式（16）代入（15）式可得，考虑政府隐性担保预期的金融机构总资产价值的运动规律：

对上式两边同时求导，可求得的微分形式为：

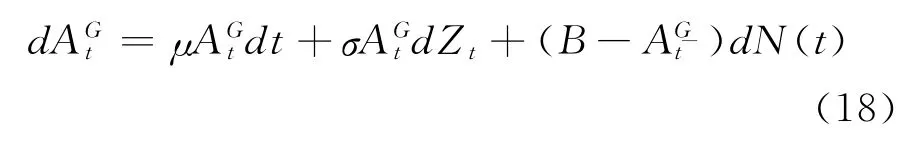
在金融机构资产价值运动服从公式（18）的条件下，当＜ρB时违约发生。设τ为金融机构违约发生的时点，且τ=inf（t｜＜ρB，t＞0），那么金融机构在其债务存续期内违约的概率可以表示为：

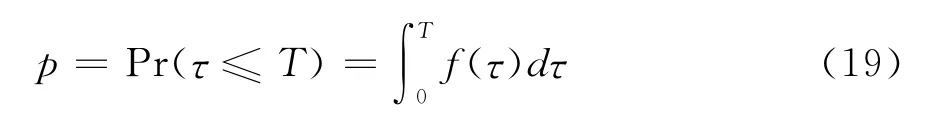
其中f（τ）表示违约时点的概率密度函数，取决于的运动过程。同时违约发生时刻金融机构的资产价值为，则相应的预期总损失现值为：

其中政府将承担的预期损失部分为：

债权人将承担的预期损失部分为：

与Zhou［22］和Merton［23］所描述的跳过程不同，在公式（18）所描述的跳过程中，连续部分与跳跃部分相关，因此偏微分方程式（18）的显性解较难求得，从而很难得出该模型下违约风险的解析解，但可通过蒙特卡洛模拟来求得其数值解。数值解的求解思路如下：（1）模拟考虑政府隐性担保预期的金融机构资产价值的运动路径。由于中连续部分服从对数正态分布，而其跳跃部分与连续部分相关，为了保证模拟的更加准确，我们设置X t=ln，通过模拟X t的过程以得到的过程。根据单个跳过程的伊藤—德布林公式可得：

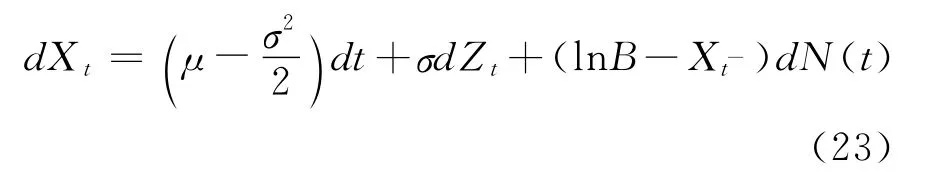
将其进行欧拉离散化，可得：

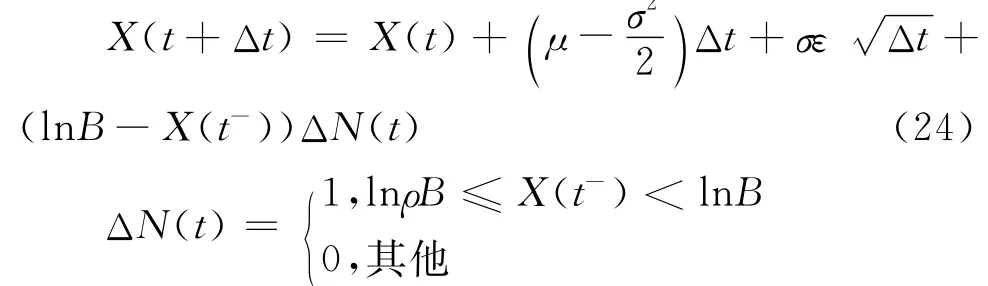
为得到［0，T］时间段内X t的运动轨迹，将时间段［0，T］平分为n等分，第k个时间点t k=T·k／n（k=0，1，2，…，n）。通过一定的参数设置，根据公式（24）利用蒙特卡洛模拟可以得到每个X（tk）的值，从而得到一条X t的路径。为了使计算结果更有说服力，需要重复上述过程M次，得到M条X的路径，在M足够大的情况下将获得稳定的结果。对于每一条路径，当X的值首次低于lnρB时停止，并记录下相应的时间τj（j=1，2，…，M）以及对应的X值X（τj），否则继续运行；（2）计算X≤lnρB的次数m并除以M得到违约概率p的数值解；（3）根据模拟信息计算得到违约时总预期损失现值P的数值解，计算得到P B的数值解，计算P-P B得到P G的数值解。

3 政府隐性担保退出下金融机构违约风险的数值计算结果

3.1 政府隐性担保退出过程中特定风险状态金融机构违约风险

针对上文提出的违约风险模型，通过一定的参数初始值设置，本文首先计算了政府隐性担保退出过程中特定风险状态金融机构违约风险的数值解。根据Merton［23］及许友传［9］等将相关参数设定如下：第一，将金融机构债务期限T标准化为1年，设置n=365，同时选择r为5%；第二，选择资产收益率μ为15%、波动率为30%、杠杆率为0.8的金融机构；第三，政府隐性担保程度ρ变动区间为［0.85，1］（Step=0.1%），该区间基本涵盖了从完全隐性担保到完全无担保的范围。同时，为了更为清晰地观察金融机构违约风险的变化，本文在数值计算过程中设置了另一变量——边际违约概率，其计算公式为，表示金融机构违约概率对政府隐性担保程度的敏感性。其值越大说明金融机构违约概率对政府隐性担保退出越敏感。

在上述参数设定下，本文利用Matlab软件进行了10万次模拟（模拟结果达到稳定状态），得到了相关变量数值解，其结果如图1所示。观察图1A 和图1B可以发现，当ρ=0.89时，金融机构的违约概率与预期损失均为0，达到完全隐性担保状态。相等于存款保险制度推出前，我国实行全额隐性存款担保时的状态［15］。当存款保险制度推出并明确了政府对存款的担保范围时，市场对政府隐性担保程度的预期将递减，从而增加对ρ值的估计。若此时市场对ρ值的估计增加到0.93，那么根据图1 可知，存款保险制度推出后，金融机构的违约概率将增加到8.23%，违约时的预期损失将增加到0.63%。当2018年资管新规颁布时，市场对ρ值的估计将再次增加，假设此时ρ值增加到0.96，那么金融机构的违约概率将增加到48.64%，同时违约时的总预期损失将增加到2.46%。可见，随着隐性担保政策的逐步取消，金融机构的违约风险将增加。具体而言，随着ρ值增加，金融机构违约概率逐渐增加并收敛于ρ=1 的情形，达到66.13%。与此同时，金融机构违约时的总预期损失呈现先递增后递减的变化过程：在ρ∈［0.89，0.96］的区间内递增，并在ρ=0.96附近达到最大值2.49%，而后递减到1.07%。

为探究政府隐性担保退出过程中预期损失呈现先递增后递减的变化趋势的原因，首先分析预期损失的影响因素。根据公式（20）可知，预期损失主要取决于金融机构违约概率p与其资产回收率A Gτ／B这两个变量相对于ρ的变动程度：当ρ增加时，金融机构违约障碍ρB与违约时资产价值A Gτ均增加，若ρB增加所带来的违约概率增量高于A Gτ增加所引起的资产回收率的增加量，那么预期总损失将增加，反之，预期总损失减少。由于AGτ随着ρ增加基本呈线性增加趋势，因此预期损失的变化取决于违约概率对ρ的敏感性。观察图1A 中边际违约概率变化趋势可以发现，随着ρ增加，边际违约概率呈现先增加后减小的趋势，且在ρ=0.95附近取到最大值。这一趋势与图1B 中总预期损失的变化趋势不谋而合。这一变化趋势暗含了市场适应政府隐性担保改革的过程：在隐性担保退出初期，市场对于担保程度递减的反应较为剧烈，表现为边际违约概率及预期损失随着ρ增加而增加；在隐性担保退出后期，市场对于担保程度减弱的反应变缓，表现为边际违约概率与预期损失随着ρ增加而减少。

另外，为探究政府隐性担保退出过程中金融机构违约风险的转移过程，本文分别计算政府及债权人将承担的预期损失部分，以及其与总损失的比值，结果如图1B和图1C 所示。从图1B 中可以看出，在0.85＜ρ＜0.96的区间内，政府所承担的损失递增且明显高于债权人所承担的损失，而且两者之间的差值随着ρ值增加而增加，并在ρ=0.96附近达到最大；在ρ从0.96增加到1的过程中政府所承担的损失递减、债权人所承担的损失递增，直到ρ=1时损失均由债权人承担。这说明在政府隐性担保退出初期，增加的预期损失将更多的由政府来承担，直到退出后期才转移至债权人。因此，为防范隐性担保取消过程中金融机构违约而引起的系统性金融风险，可根据该过程中政府承担的预期损失值，建立时变的金融机构流动性缓冲，以吸收担保预期转变产生的潜在损失。结合存款保险推出后0.93的ρ值估计可知，此时政府针对这一特定的金融机构应设立0.56%的流动性缓冲，而在资管新规颁布后流动性缓冲应增加为1.19%。

图1C更为直观地展现了政府隐性担保退出过程中金融机构违约风险转移过程：ρ处于0.86附近时，政府承担损失比重接近于1，债权人所承担部分几乎为0；随着ρ的增加政府承担比重逐渐减小、债权人承担比重逐渐增加，在ρ=0.985附近时相等；ρ=1时损失全部由债权人承担。即随着政府隐性担保退出，金融机构的违约风险逐步从政府部门转移至债权人。

图1的结论仅体现了政府隐性担保退出过程中特定杠杆率与特定波动率下金融机构违约风险的变化，那么当金融机构的风险状态变化时，其违约风险的变化是否与上述情况一致呢？为了回答这一问题，接下来本文计算并分析了政府隐性担保价值转变过程中不同杠杆率与不同波动率下金融机构的违约风险。

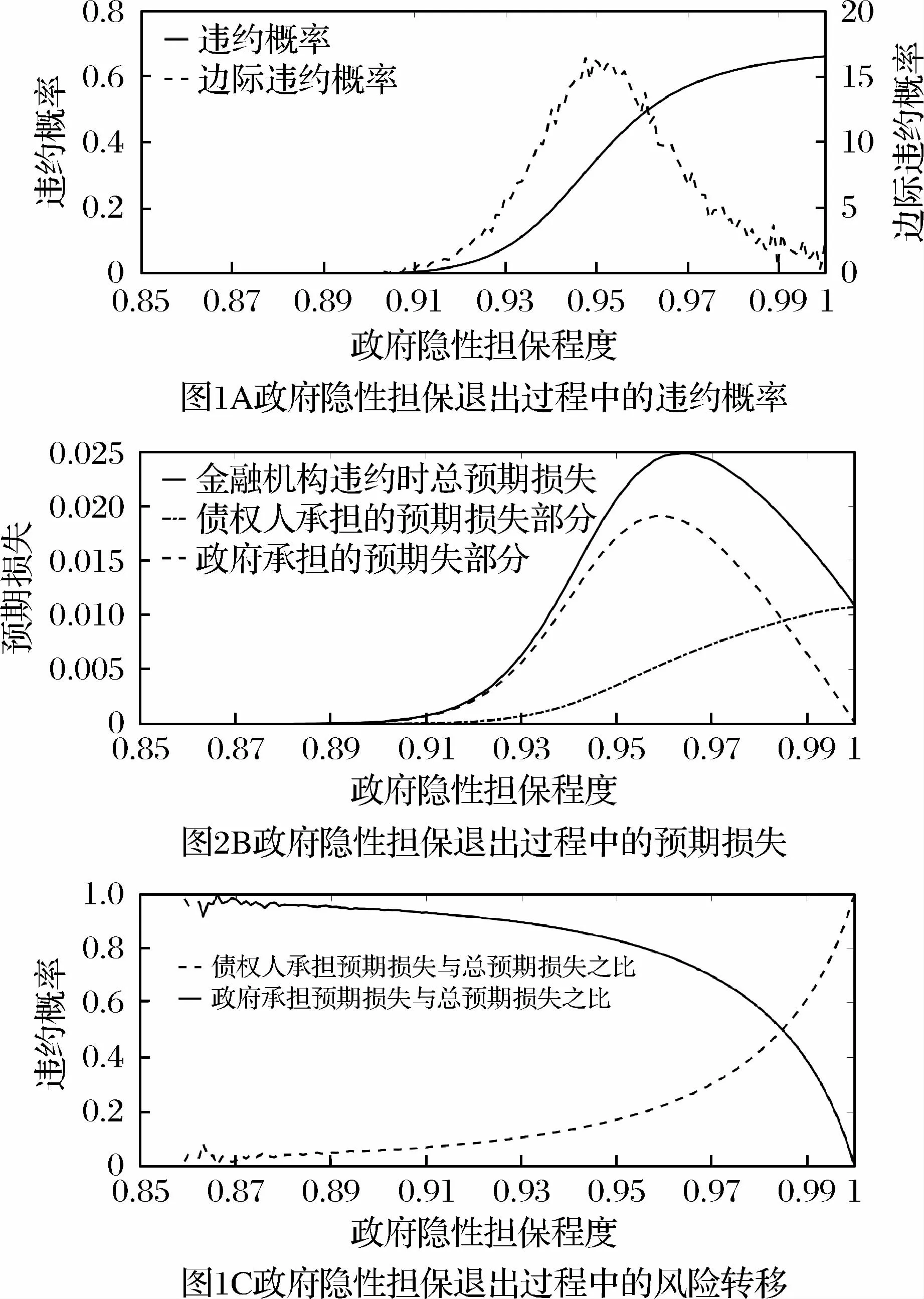
注：图1B的预期损失为除以总负债后的值（下同）。

3.2 隐性担保退出过程中不同杠杆率下金融机构违约风险

本部分将分析杠杆率对隐性担保退出过程中金融机构违约风险的影响。为此，我们在保持其他参数值不变的情况下，改变B值再次进行估计。为了涵盖绝大多数可能的合理情形，这里设置金融机构总负债的变化范围为20 到80，在A0不变的情况下，这表明杠杆率的范围为［0.2，0.8］，经过多次模拟得到的稳定结果如图2所示。由图2 可知，在ρ值增加过程中，不同杠杆率下金融机构违约风险的变化趋势相同但违约风险的绝对大小却有显著差异。在ρ从0.85增加到1的过程中，杠杆率越高，金融机构违约概率越大，对政府隐性担保程度递减的敏感性越强，预期损失及其所能达到的最大值越大。如当杠杆率为40%时，金融机构预期损失最大值为负债总额的0.29%；当杠杆率为60%时，金融机构预期损失最大值已达到负债总额的1.07%。说明杠杆率越高的金融机构在政府隐性担保退出过程中违约的可能性越大。

同时由图2A 可知，在本文的参数初始值设置下，当金融机构的杠杆率处于［0.2，0.7］的范围内时，其违约概率在政府隐性担保退出过程中均小于50%。因此，若以50%的违约概率作为金融机构违约可控点，那么杠杆率小于0.7的金融机构将不会因政府隐性担保退出而违约。基于此，为防范系统性金融风险，在政府隐性担保退出前对金融机构降杠杆是必要举措。同时基于本文的参数设置，应将金融机构杠杆率降到0.7以下。

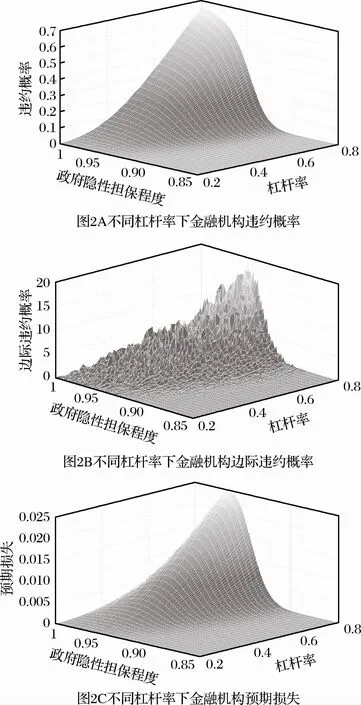
注：图2的计算结果建立在以下参数初始值设置的基础上：A 0=100，μ=0.15，σ2=0.3，r=0.05，同时设置B 的变化范围为20到80，在A 0 不变的情况下，这表明杠杆率的范围为［0.2，0.8］。

3.3 隐性担保退出过程中不同波动率下金融机构违约风险

在其它参数值不变条件下，将金融机构资产波动率变动区间设置为σ2∈［0，0.3］（Step=0.5%），本部分计算了政府隐性担保退出过程中不同波动率下金融机构的违约风险，经过多次模拟得到的稳定结果如图3所示。

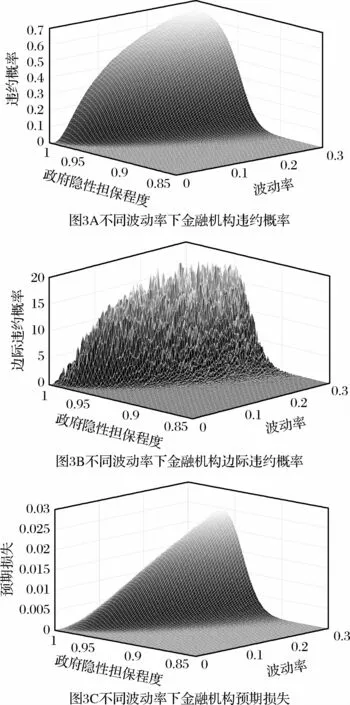
注：图3 结果建立在以下参数设置的基础上：A 0=100，μ=0.15，B=80，r=0.05，σ2∈［0，0.3］。

与杠杆率的影响类似，波动率的变化对于政府隐性担保价值退出过程中金融机构违约风险的变化趋势没有较大的影响，但是其对于金融机构违约风险的绝对大小却有显著的影响。在ρ从0.85增加到1的过程中，随着金融机构波动率的增加其违约概率、边际违约概率及预期损失均递增，同时预期损失所能达到的最大值之间也有明显差别，如当σ2=0.1时，预期损失最大值为负债总额的0.72%；当σ2=0.3时，其最大值将达到负债总额的2.50%。说明在政府隐性担保退出过程中，金融机构的资产波动率越大，其违约可能性越高。

Panageas［20］指出在存在政府隐性担保的情况下，金融机构为追求利益最大化往往会将资产投资于具有高风险的项目，使其资产波动率处于高位。结合金融机构资产波动率越高，在政府隐性担保退出过程中违约可能性越大的研究结果，为防范系统性金融风险，本文建议在完全打破政府隐性担保前，应降低金融机构的资产波动率。由图3A 可知，当金融机构的资产波动率σ2∈［0，0.16］的范围内时，金融机构的违约概率在政府隐性担保退出过程中将不会超过50%。因此，基于50%的违约可控点，在本文的参数设置下，应在完全打破政府隐性担保前，保证金融机构波动率不超过0.16。

4 结语

存款保险制度的建立、资管新规的颁布均意味着政府将逐步退出其对金融机构的隐性担保，而这将冲击现有体系内隐性担保预期，引起金融机构违约风险重定价。基于此，本文构建了考虑政府隐性担保预期的金融机构违约风险模型，模拟了政府隐性担保退出过程中金融机构违约风险的变化。通过分析得出以下结论：

（1）在政府隐性担保退出过程中，金融机构的违约概率逐渐增加，违约时的预期损失呈现先增加后递减的趋势，且在担保退出初期增加的预期损失更多的由政府来承担，直到后期才转移至债权人。

（2）金融机构的波动率越大，杠杆率越高，在政府隐性担保退出过程中其违约概率与预期损失越大。

为防范政府隐性担保退出过程中因金融机构违约引起的系统性金融风险，坚守不发生系统性风险底线，基于上述结论，本文得到以下政策启示：

（1）根据隐性担保退出过程中政府将承担的预期损失值，建议时变金融机构流动性缓冲，以吸收打破担保而引起的潜在损失。

（2）在完全打破隐性担保前，应对金融机构实施降杠杆与降波动。基于本文的参数值设置，可将杠杆率与波动率分别降到0.7与0.16以下。