通胀对高管的股权激励和工作努力策略的影响
费为银,张繁红,3,杨晓光
(1.安徽工程大学数理与金融学院,安徽 芜湖 241000;2.中国科学院数学与系统科学研究院,北京 100190;3.上海财经大学数学学院,上海 200433)
1 引言
对公司治理理论中的激励机制的研究一直是学术界的重要研究方向。根据委托代理理论,为了解决由信息不对称产生的道德风险问题,从契约双方共同利益的角度,企业所有者制定的股权激励机制能够有效激励和约束高管的行为。吴崇和胡汉辉[1]研究表明,基于企业战略机会评价,公司制定的激励机制发挥了对高管的导向作用,在协同企业战略和激励的同时,引导高管平衡战略投资和经营投资管理。过去的文献主要探讨的是高管的股权、薪酬和公司业绩之间的相关关系[2-4],其中股权激励机制受到广泛关注。
Dittmann和Maug[5]利用标准的委托代理有效合同模型来研究高管获得的补偿的合理性,发现高管不会获得期权式补偿,但高管会以个人财富购买所在公司的股票。Jensen和Murphy[6]研究发现高管的薪酬绩效的敏感度受到管理人才市场的固有观念的影响和约束,于是导致大部分CEO 持有少量的所在公司的股票。Hall和Liebman[7]与Core 和Larcker[8]表明CEO 股权式补偿的获得和公司绩效间存在着相关性。Ai和Li[9]使用新古典投资模型验证了CEO 的薪酬模式与以往绩效存在相依关系。本文试图在动态规划模型下研究股权激励的框架。
对于得到股权激励的高管,无论高管的绩效薪酬是否受到业绩条件的约束,高管的业绩补偿都将全部反映在个人财富中,并且高管对个人财富会进行优化分配。刘银国等[10]研究了高管的股权激励与盈余管理模式选择问题,发现高管的股权激励的预期效果受到行权业绩条件的影响。Bettis等[11]调查发现为了避免股权式补偿的约束,高管通常在外部市场上利用领式期权或者掉期交易方式对持有的公司股票进行套期保值。Ofek和Yermack[12]表明当高管持有的公司股票达到一定水平时,高管不仅会获得股权分红收益,而且会对个人的投资组合进行重新优化。并且Garvey和Milbourn[13]研究发现高管对个人投资组合的优化调整可以实现风险规避,结果表明持有公司股票的高管的投资组合收益几乎不受市场风险的影响。Bolton等[14]发现风险厌恶企业家的净资产过度暴露于非系统风险之下,而对系统性风险的敞口则较低。从以上文献结果分析,现实中为了规避所在公司股价的不确定风险,持股高管会主动在市场中配置其他资产账户以优化个人投资组合,因此本文在构建高管的总体资产模型时,考虑到了银行无风险资产账户与市场投资组合账户。
在构建高管的资产价格动态模型时,公司的股票价格过程受到高管的工作努力策略的影响。Cadenillas等[15]构建了高管的资产动态的随机模型,其中控制变量包括高管的工作努力参数和公司股票价格过程的波动率。Desmettre等[16]研究了一致连续时间上的高管股权激励和工作努力策略的基本框架,其中高管的工作努力策略表现为公司股票价格过程的夏普率,但在构建高管资产组合模型时,没有考虑市场存在的不确定因素对资产价格的影响。
考虑到高管在实际个人资产会受到市场通胀不确定的影响,本文对高管的名义财富过程进行通胀折现来得到真实的财富过程,并把预期的终端真实财富效用最大化作为高管的目标。从20 世纪70年代的以来研究文献看,在研究动态投资组合最优化问题时,许多学者考虑到了市场中的通胀因素。Brennan和Xia[17]考虑到市场环境存在的通胀风险,利用鞅方法研究了动态投资组合最优化问题。Siu[18]在研究长期战略资产配置问题时引入了市场中存在的通胀风险因子,并利用鞅方法得到了配置策略的优化方案。基于Brennan和Xia[17]的研究,姚海祥等[19]采用连续时间均值-方差模型,在通胀环境下研究了投资组合最优策略问题。Wang等[20]发现在不完全市场下,企业家流动性资产和风险管理受到非系统风险溢价的影响。费为银和李淑娟[21]以及梁勇等[22]研究了通胀和Knight不确定因素对最优投资组合策略的影响。费为银等[23]研究了含糊厌恶的投资者的最优投资组合问题,并且同时考虑了通胀和极端事件冲击的影响。费为银等[24]在递归效用情形下,利用动态规划原理,得到了带通胀的最优消费与投资组合策略。费为银等[25]在通胀环境下,研究了存在激励的对冲基金经理人的投资组合的最优策略问题。费晨等[26]从概率统计模型存在的不确定性的角度,研究了代理人的道德风险对契约的执行过程和契约存续情况的影响。随后费为银等[27]研究了在Knight不确定下单边有限承诺的最优契约设计问题。李爱忠等[28]研究了通货膨胀、随机利率和交易成本等因素影响下的连续时间投资组合选择的最优化问题。
通过对上述文献分析,发现目前的研究重点主要为股权激励效用与公司业绩的相关性,但事实上,公司对高管的股权激励应该首先对高管产生影响,进而影响公司业绩。在市场环境存在通胀不确定因素下,不同特质的高管会采用不同的行为模式,那么公司该如何建立针对不同特质高管的激励合同,相关方向值得研究。本文构建了动态随机模型,随后利用随机控制理论和方法推导出高管的最佳个人投资和工作努力策略,并分析了不同特质高管的预期行为,为公司与高管建立激励合同提供了参考。本文以公司中高管的股权激励研究为基础,结合我国市场通胀的实际情况,分析了在通胀下高管的股权激励和工作努力策略问题,对企业中股权激励制度对高管的行为影响尽可能的进行了研究。
2 金融市场基础框架
本文在Desmettre等[16]研究的框架基础上,引入通胀动态方程。金融环境中的三个布朗运动Zt,和定义于带流概率空间 (Ω,F,(F t)t≥0,P),其中Z t定义为通胀下的随机状态,和分别为市场投资组合价格过程与公司股票价格过程的相应随机状态,并且。高管的投资组合账户包括:公司股票资产账户,银行无风险资产账户和市场投资组合账户。其中银行无风险资产的名义价格 ()t≥0为:
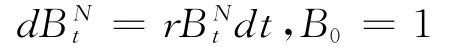
其中r表示银行无风险利率;投资于市场投资组合的名义价格为满足:

其中市场投资组合的预期回报率和预期波动率分为μP和σP;投资于公司股票的名义资产账户为:

(1)式中常数β∈R+为高管所在公司的贝塔系数,μS表示非系统预期回报率,σS为非系统预期波动率。高管的名义控制策略为 (μS,σS)。
于是高管的名义财富过程为:

考虑到市场通胀因素对高管的名义财富的影响,引入通胀动力学方程:
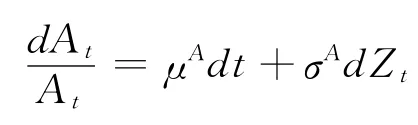
其中μA为预期通胀率,σA为预期通胀波动率。利用伊藤公式得:

设高管在t时刻的真实财富过程V t由等式演变,利用伊藤公式得:
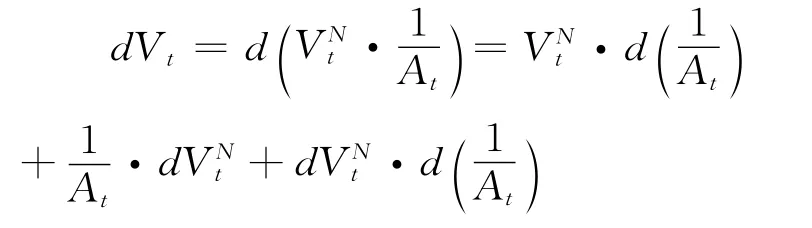
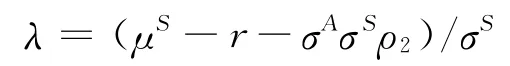
高管的名义财富过程为:
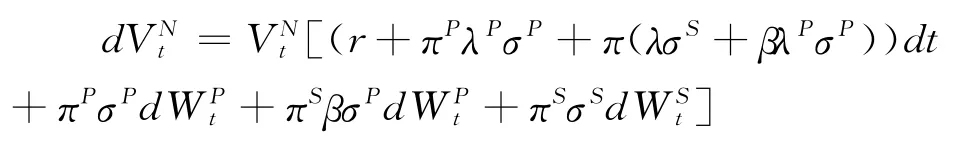
整理得到高管的真实财富过程为:
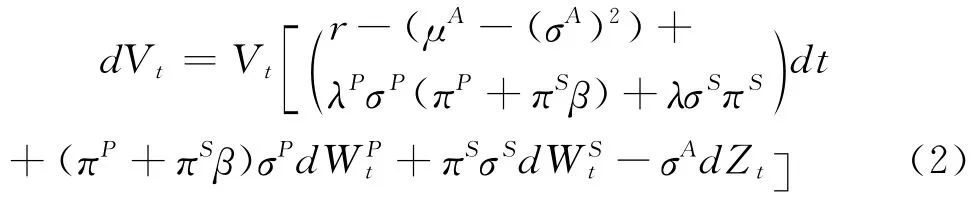
另一方面,考虑到高管会因工作而产生效用损失,表示为c(t,v,μS,σS),并且c:[0,T]×R+× [r,+∞]×R+→R+是一个的连续函数,由于λ可以表示为 (μS,σS)的函数形式λ=(μS-r-σAσSρ2)/σS,那么基于Desmettre等[16]中引理1 对高管的工作效用损失的分析,这里类似有存在且唯一的σ*(t,v,λ),并且以λ为变量的负效用函数在t时刻满足:
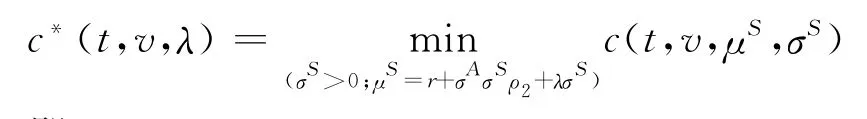
即
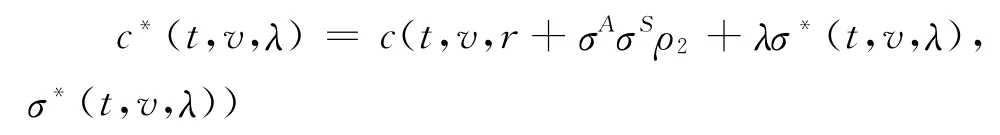
这里,σ*(t,v,λ)表示使得高管工作效用损失最小的公司股票价格过程的波动率。为确保工作努力控制策略的最优,我们将σ*(t,V t,λ)替换(2)式中σS。
于是得到高管的最优投资组合与工作努力控制策略问题的值函数为:
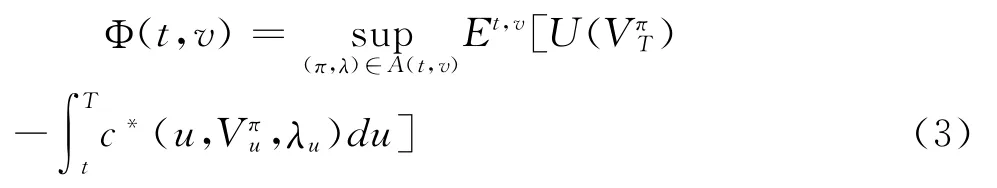
其中V t=v,(t,v)∈ [0,T]×R+,A(t,v)表示{F u:t≤u≤T}域流上t时刻的投资组合和工作努力控制策略的集合。
3 最优策略
与Desmettre等[16]对财富效用函数的设置一致,考虑通胀折现后,本文对高管真实财富过程分别在经典的效用函数和工作负效用函数的模型下进行分析。高管的特质参数γ表示他的风险厌恶程度。针对不同的风险厌恶的高管,真实财富效用函数U为:

工作负效用函数为:
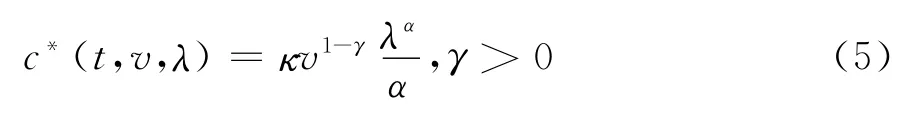
其中κ>0与α>2分别表示高管的逆工作效率参数与负效用强度参数,在后文中得到的最优工作努力控制策略λ与κ,α直接相关。α>2表示工作产生的负效用与工作努力水平的指数增长关系。真实财富效用与工作负效构成高管的总体效用,高管的目标是个人真实财富终端预期效用最大化。
与Desmettre等[16]一致,风险厌恶γ与高管的职业水平相关。直观上,当γ=1时,他的财富效用服从对数函数,且工作负效用与财富无关。风险厌恶程度较低(0<γ<1)的高管职业素养和水平都较高,而且财富的增长会为高管带来激励作用;而对于风险厌恶程度较高(γ>1)的高管则较复杂,财富的增长并未带给高管激励作用,而且此时财富v增长,那么高管工作努力水平提高,但v1-γ减小,所以无法判定效用损失c*(t,v,λ)的增减趋势。与Desmettre等[16]一样,本文讨论了幂效用情形 (γ>0,γ≠1)和对数效用情形 (γ=1)。
利用动态规划原理得到带有股权激励的高管最优投资组合与工作努力控制策略问题(3)的HJB方程为:
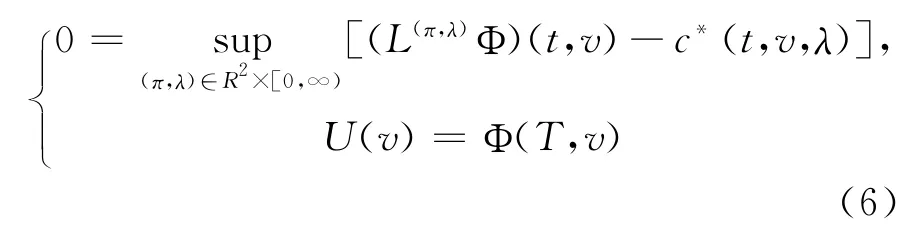
其中 (t.v)∈ [0,T]×R+,v∈R+。算子L(π,λ)的形式如下

解(6)式得高管财富的最优投资资产比例πP*与πS*为:
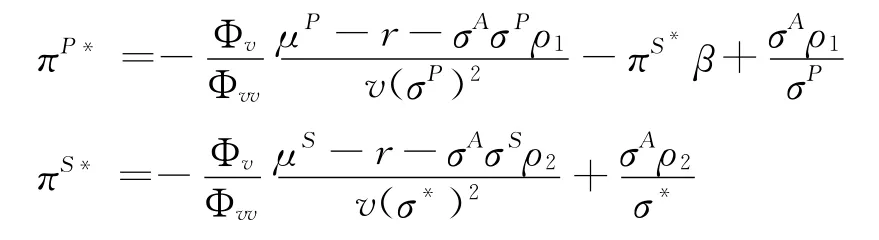
通胀下由高管控制的最优工作努力策略夏普率λ的隐式方程为:

将πP*和πS*带入(5)式得:

注意到因为市场产生的通胀来自于宏观调控,对于单个公司的股价来说这种影响很小,所以后文的解析解和数值模拟中相关系数ρ2=0。
定理1在幂效用情况下(γ>0,γ≠1),得到最优化问题(3)的解为:
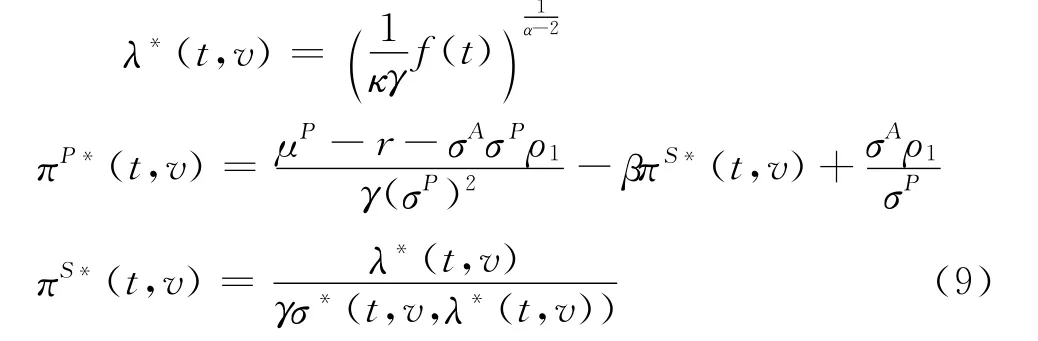
价值函数为:
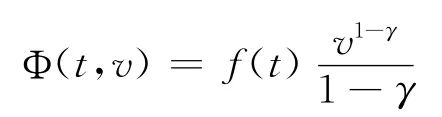
其中
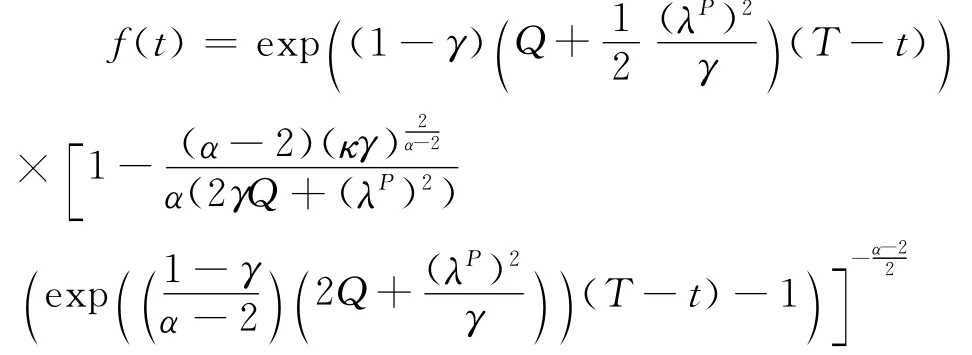
这里
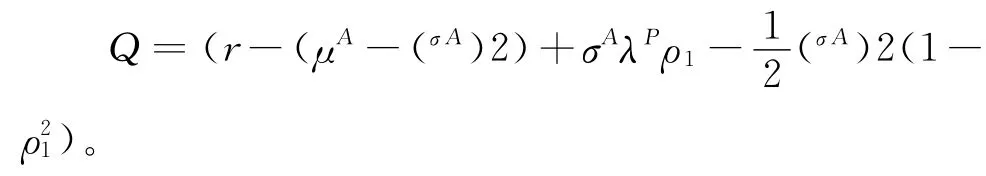
证明首先分析函数F(λ)=aλ2-bλα,其中给定a>0,b>0,α>2且有唯一的最优解λ*和最大值F(λ*),分别为:
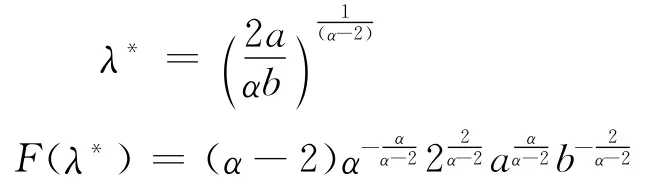
将最优解λ*代入(7)得到,于是有:
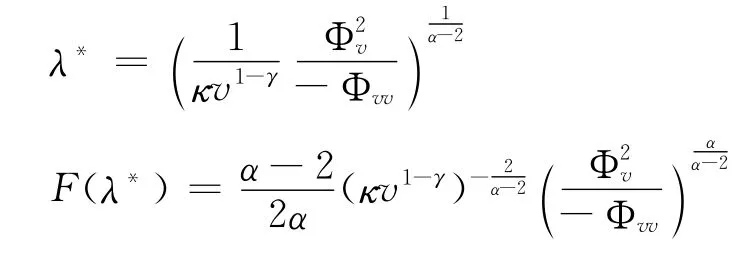
那么(8)式变为:

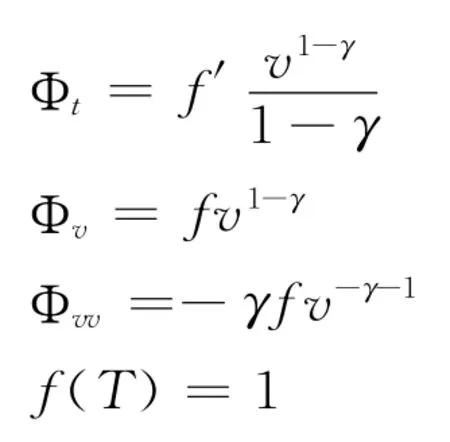
并代入(10)得:

化简得:

于是可得f(t)的表达式。至此,定理1证毕。
定理2财富效用服从对数函数时,解问题(3)得:
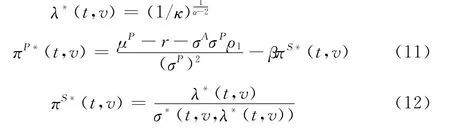
价值函数为:

证明:将函数F(λ)=aλ2-bλα的最优解λ*和最大值F(λ*)代入(7),有,于是得到:

对数效用下的(7)式变为:
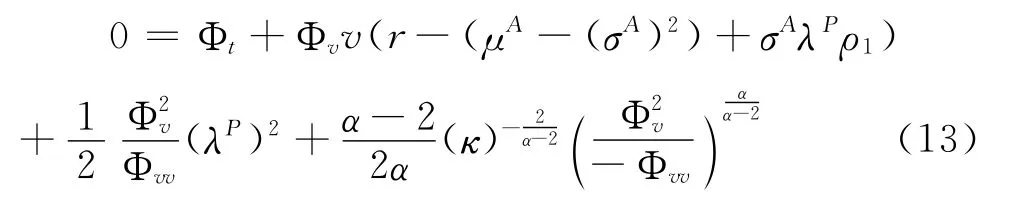
假设价值函数
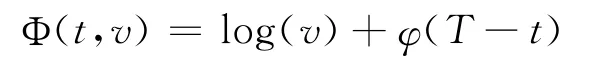
为了更直观反映现实情形,本文对高管的工作努力水平设定基础值λ0>0。λ*表示契约期限最高T内高管最优工作努力策略,引入基础参数λ0后,得到的负效用函数变为:
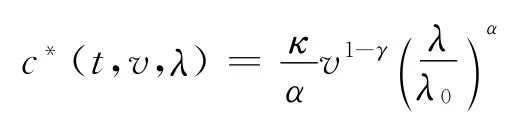
根据定理2,对数效用下高管的最优工作努力控制策略的解为:

为符合基本的工作努力控制策略要求λ*≥λ0>0,于是有1/κ>。
根据定理1,幂效用情形下最优工作努力控制策略的解为:

其中

根据定理1的最优解(9)和(15),高管个人财富中的公司股票账户的最优投资比例为:

4 数值分析与经济学解释
定理1 和2 得到了在不同预期财富效用函数(以高管的风险厌恶程度作为区分依据)下问题(3)得到解析解。接下来研究通胀对高管的股权激励和工作努力策略的影响,在分析时将工作努力策略直观化为工作努力水平。数值模拟中给定银行无风险资产账户的利率r=5%,市场投资组合账户的预期回报率μP=7%,市场投资组合的预期波动率σP=20%,布朗运动相关系数为ρ1=1,预期通胀率为μA=6%,基础工作努力水平为λ0=0.10。对于高管价值函数不同的效用情形,我们利用Matlab软件对(14-16)进行模拟运算和定量分析,并就结果给出对应的经济意义上的解释。
高管个人投资组合中公司股票账户的最优比例的表达式分别为(9)式和(12)式,与公司股票价格过程的预期波动率σ*存在相依性。为了利于定量分析通胀风险因子和高管个人投资组合中的公司股票账户的最优比例之间的关系,这里给定公司股票价格过程的波动率σ*=40%。
4.1 在对数效用情形下(高管风险厌恶参数γ=1)
由(14)式模拟图1和图2。图1显示最优工作努力水平λ*与工作效率1/κ正相关。图2表示由于工作负效用强度α增大,高管的工作努力水平λ*会逐渐降低。本文的(14)式与Desmettre等[16]相同情形下的结果形式上是一致的,但从微观经济学的角度分析,对数效用下的最优投资策略对公司来说是“急功近利”的短视行为。具体的可以由(14)和(12)分析出公司股票占高管个人财富的最优比例与通胀风险因素无关,但是根据(11),高管财富中市场投资组合的最优比例是随通胀波动率的增加而减小,从而影响了公司股票占高管个人财富的最优比例,进而影响高管的个人财富的投资策略。

图1 在不同工作负效用强度下高管工作努力最优策略λ* 与工作效率1/κ的关系
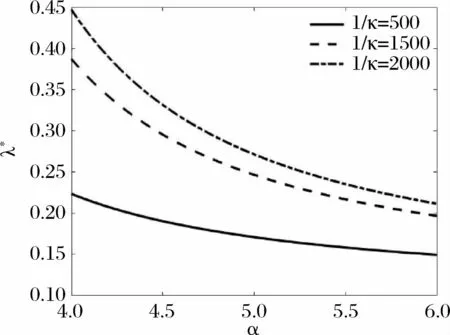
图2 在不同工作效率下高管工作努力最优策略λ* 与工作负效用强度α的关系
4.2 在幂效用情形下(高管风险厌恶参数γ>0且γ≠1)由于
由(15)式和(16)式绘制的图3-图8,工作效率参数1/κ=2000,工作负效用强度参数α=5。图3-图6中时间t=5,图7和图8选取的预期通胀波动率σA=15%。图3 表示在风险厌恶程度较低时(0<γ<1),横向观察到工作努力水平是随着风险厌恶的增加而逐渐降低。而从纵向来看,工作努力水平随着通胀波动增加而提高,这种情形下高管对通胀风险表现为近乎喜好的程度。图4表明对于风险厌恶程度较高的高管(γ>1) ,市场中通胀波动率的增强导致工作努力水平也呈下降。从图5和图6看出,当风险厌恶程度较低 (0<γ<1) 的高管的工作努力水平与最优持股比例几乎不受通胀率的影响,表明高管看好公司股票,且对通胀对公司股价的影响持乐观态度;而风险厌恶程度较高(γ>1) 的高管则相反。由图7和图8的对比可以看出风险厌恶程度较高(γ>1) 时,高管的工作努力水平变化幅度较大。
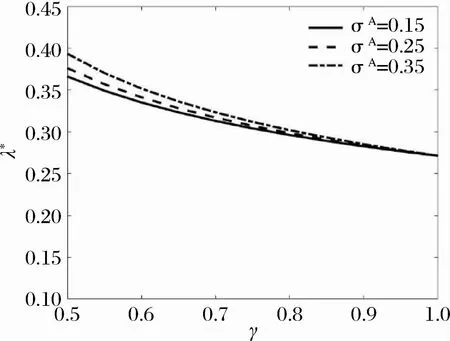
图3 不同预期通胀波动下工作努力最优策略λ* 与风险厌恶参数γ的关系

图4 不同预期通胀波动下工作努力最优策略λ* 与风险厌恶参数γ的关系
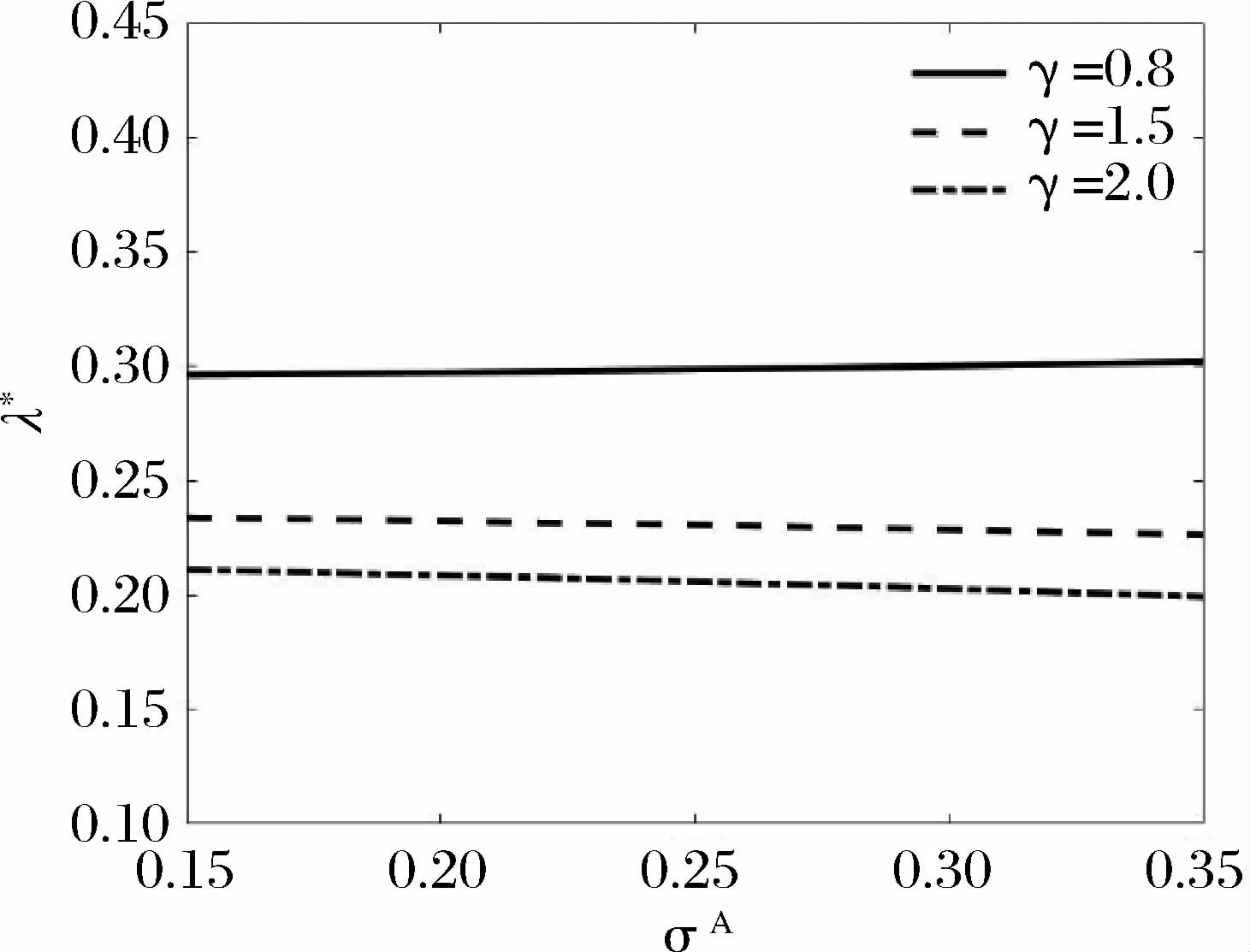
图5 差异风险厌恶程度下工作努力最优策略λ* 和预期通胀波动率σA 的关系

图6 差异风险厌恶参数下最优持股比例πS* 和σA 的关系

图7 工作努力最优策略λ* 随风险厌恶参数γ和时间的关系

图8 工作努力最优策略λ* 随风险厌恶参数γ和时间的关系
由(15)式和(16)式模拟的图9-图12,负效用强度参数和风险厌恶参数分别为α=5和γ=2,图9-图11中时间参数t=5,而图12中预期通胀波动率为σA=15%。从图9-图11表明高管的工作努力水平是随工作效率的增加而提高。当市场通胀波动率增大时,高管的最优工作努力水平与最优持股比例都呈现下降趋势,直观理解为高管谨慎地应对通胀风险。高管的较高工作效率对应着较高的工作努力水平,当通胀风险变大时,高管降低持股比例。图12表现高管的工作努力水平与工作效率正相关。由(15)式和(16)式绘制的图13-图16,选取工作努力参数1/κ=2000,高管的风险参数γ=2,图13-15中高管任期时间为t=5。图16中预期通胀波动率σA=15%。图13-15表现随着工作负效用强度的增加,高管的工作努力水平呈下降趋势。纵向来看,市场通胀波动率变大时,为规避风险,高管的最优工作努力水平与最优持股比例缓慢降低,直观上高管对通胀持谨慎态度。图16表现高管工作努力最优策略随工作负效用强度的增加而减小。
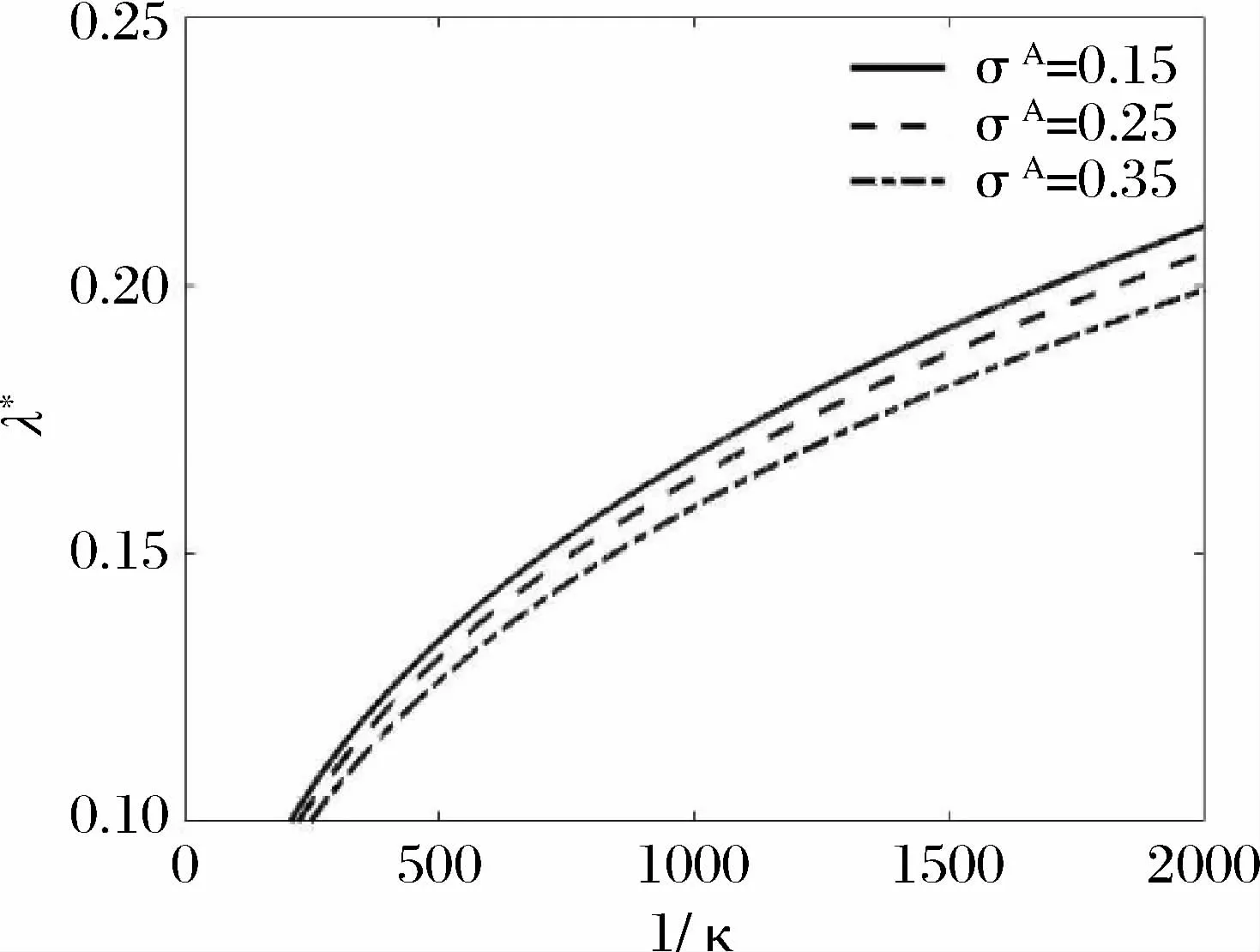
图9 不同预期通胀波动下高管工作努力最优策略λ* 与工作效率1/κ的关系

图10 不同工作效率下高管工作努力最优策略λ* 与预期通胀波动率σA 的关系

图11 差异工作效率情形下最优持股比例πS*和预期通胀波动率σA 的关系

图12 高管工作努力最优策略λ* 随工作效率1/κ和时间的关系
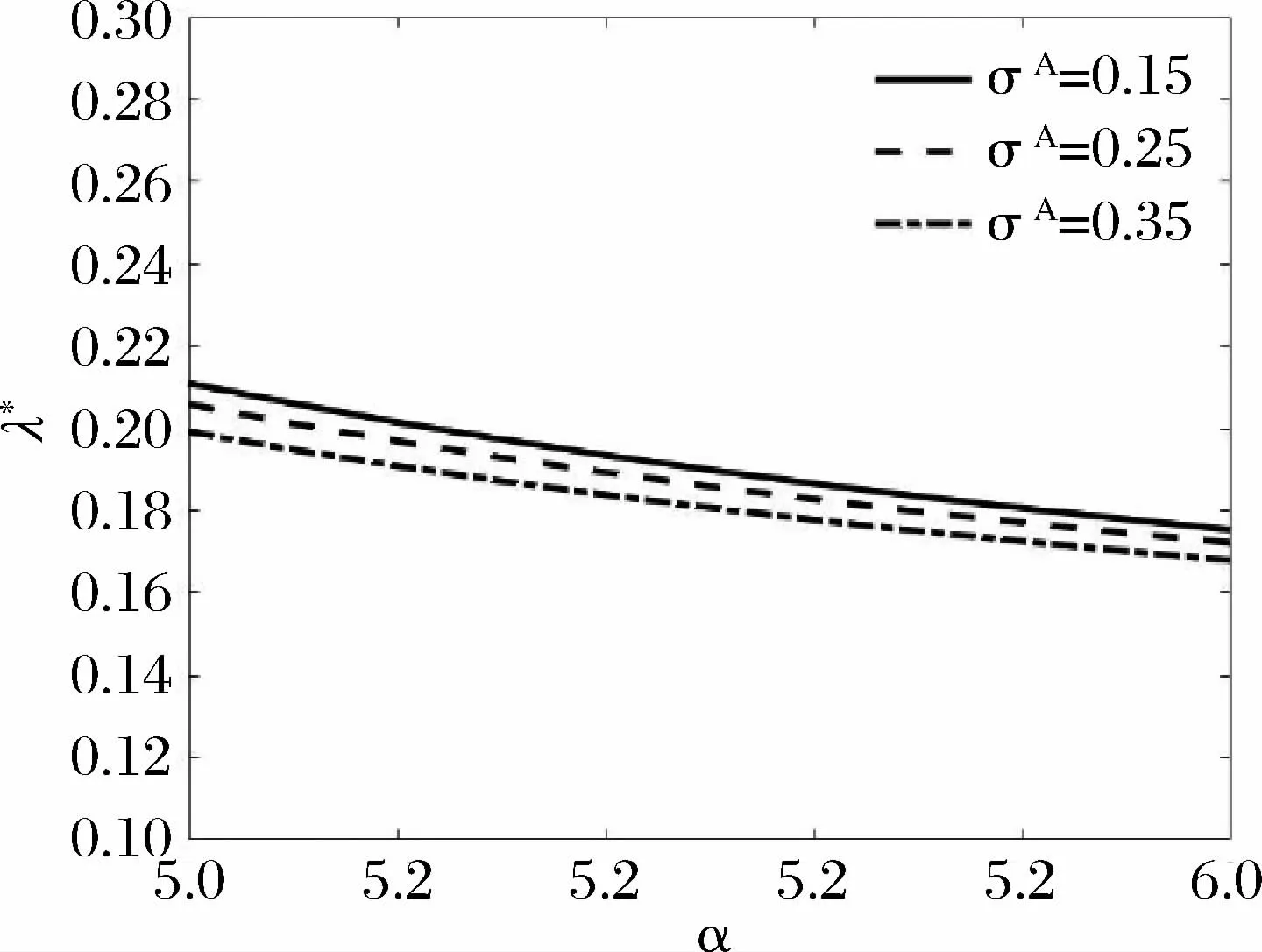
图13 预期通胀波动率σA ,最优工作努力水平λ* 和工作负效用参数α的关系
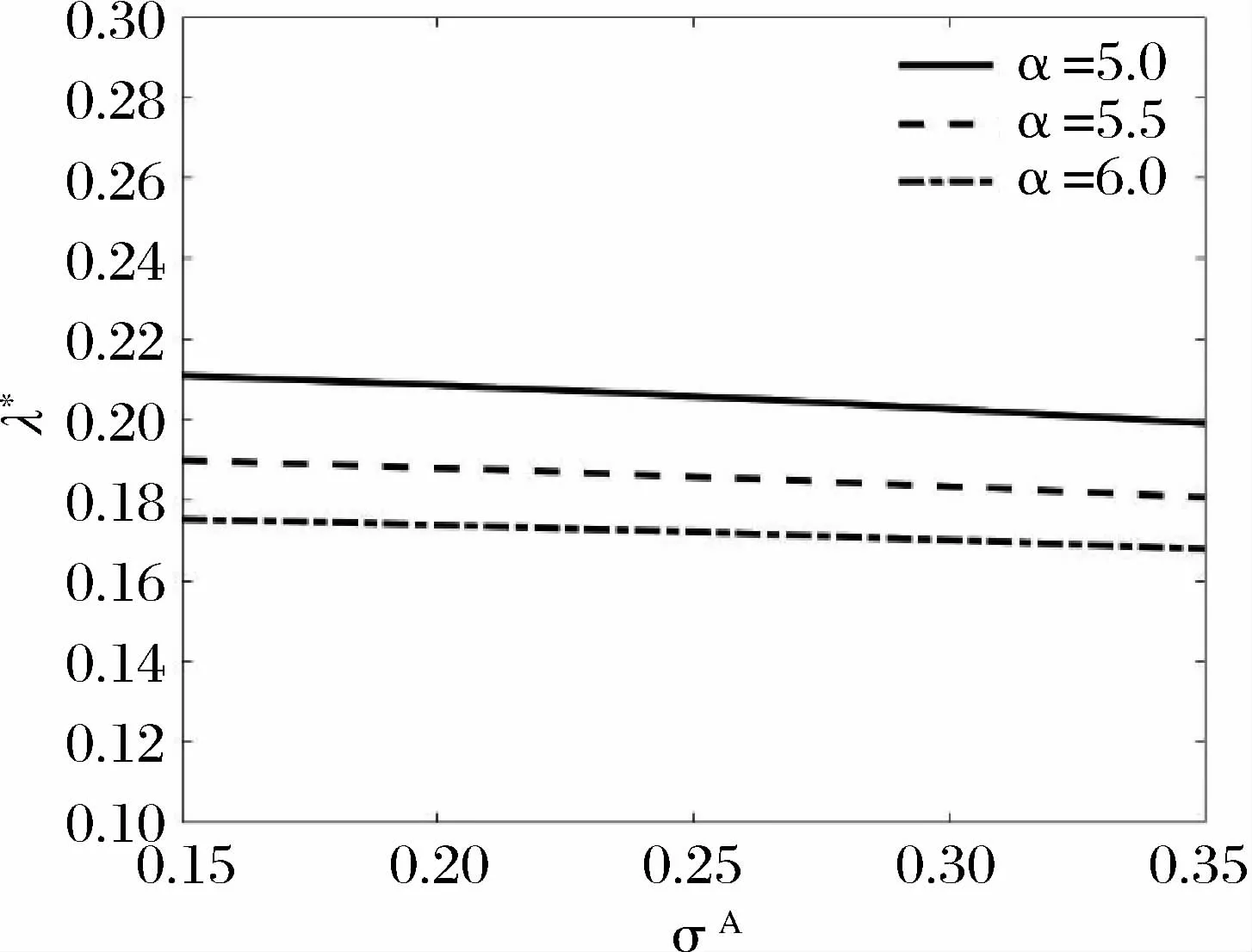
图14 工作负效用强度参数α,最优工作努力水平λ*和预期通胀波动率σA 的关系

图15 不同工作负效用强度下最优持股比例πS* 和预期通胀波动率σA 的关系

图16 高管工作努力最优策略λ* 随工作负效用参数α和时间的关系
由(15)式和(16)式模拟的图17-图22,选取工作效率参数1/κ=2000,风险厌恶程度为γ=2和工作负效用参数为α=5。图17 和图18 短期契约执行中市场通胀风险的增大,会导致高管的最优工作努力水平与最优持股比例降低,这是因为短期契约缺少长远的共同利益,通胀风险的提高使得高管对持有的公司股票进行套现。而图19和图20表明,长期契约则情形相反,这是因为长期的共同利益诱导高管看好公司的发展前景。图21和图22表现高管的最优工作努力水平与公司股票占高管个人财富的最优比例都是随契约期限的延长而提高,直观上理解为长期契约能够诱导高管从长远利益的角度出发,减少短期套现的可能。另一方面当市场预期通胀波动较小时,从图21和图22观察到高管付出较高的工作努力水平,并且最优持股比例也较高。
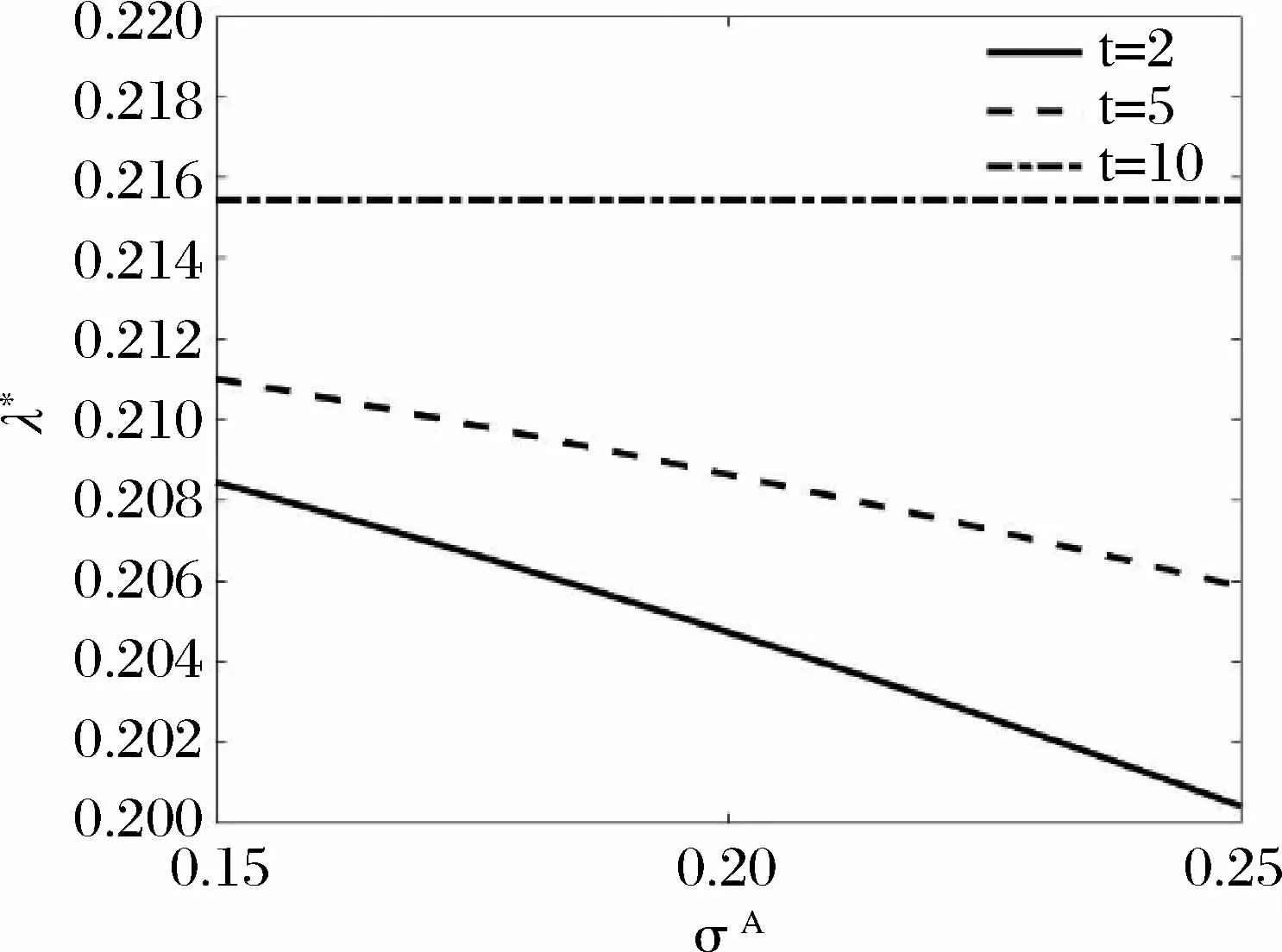
图17 在不同时间内高管的工作努力最优策略λ* 和预期动σA 的关系
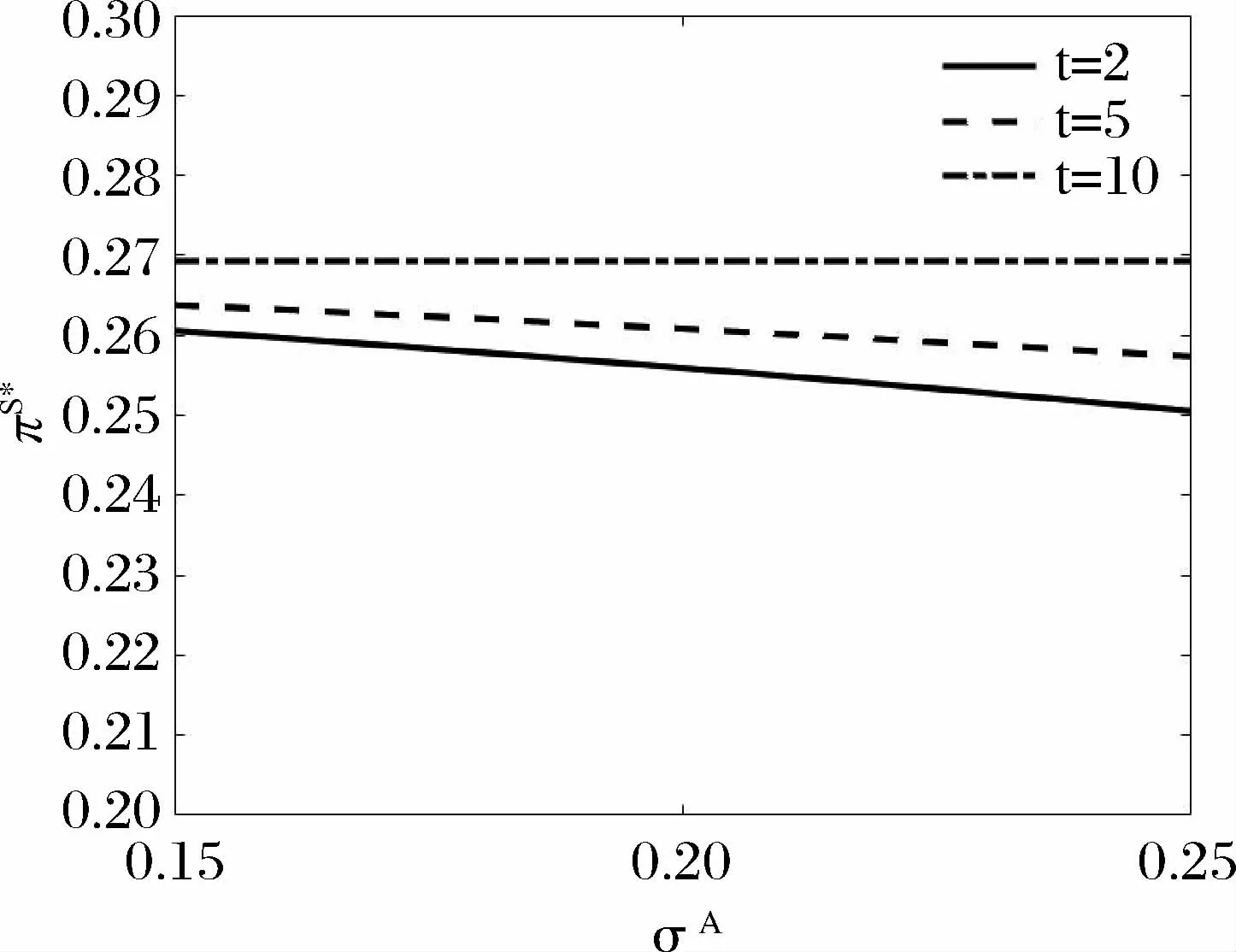
图18 不同契约期限最优持股比例πS* 与预期通胀波动率σA 的关系
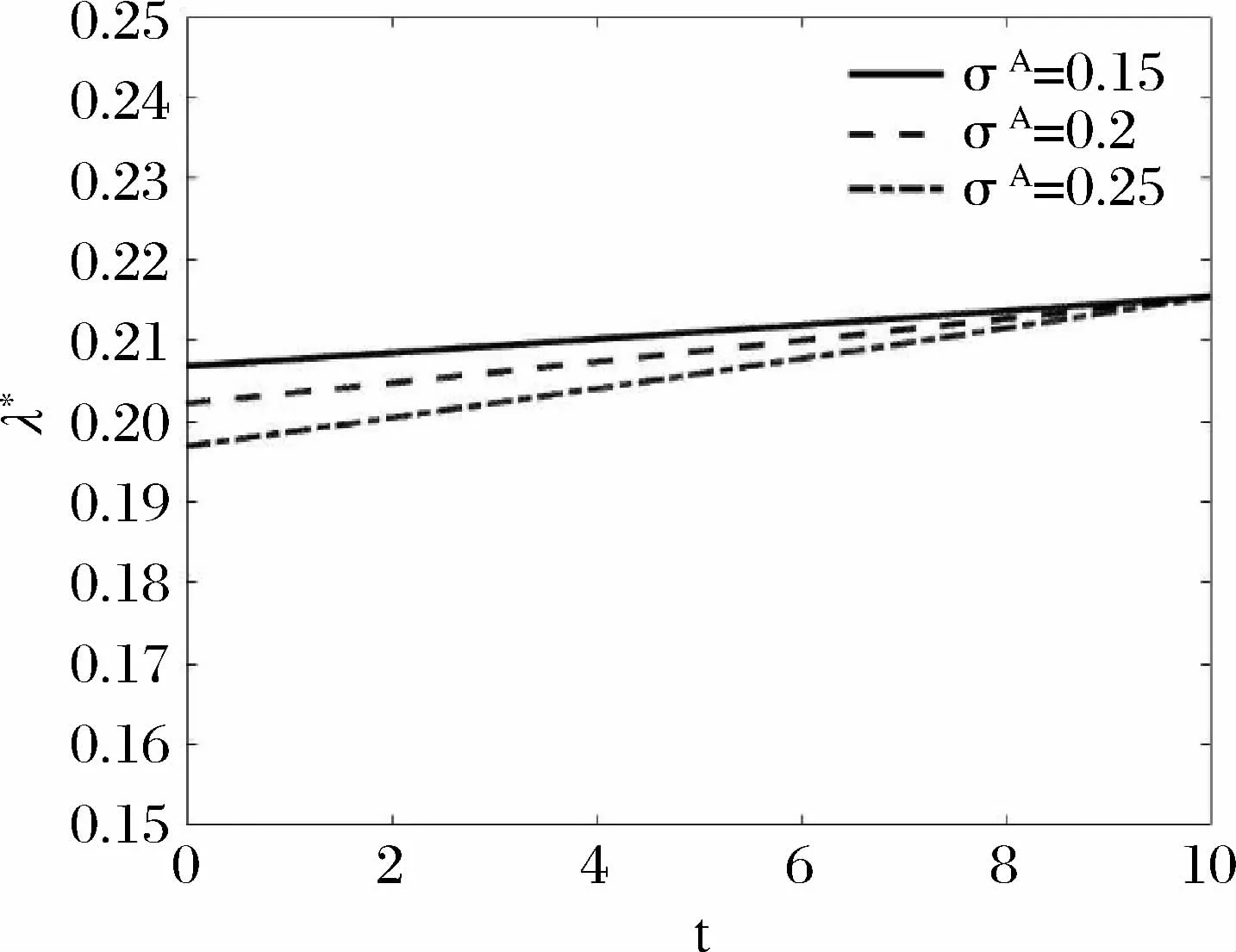
图19 不同预期通胀波动σA 下高管的工作努力最优策略λ* 与时间的关系
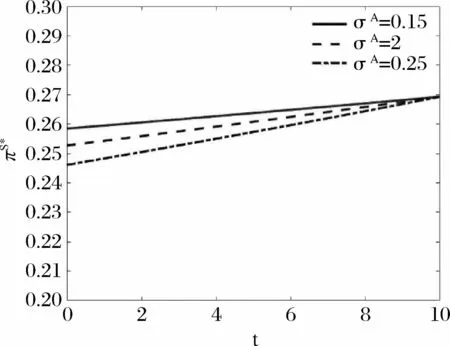
图20 不同预期通胀波动σA 下最优持股比例πS* 与时间的关系

图21 高管的工作努力最优策略λ* 随预期通胀波动σA 和时间的变化关系

图22 最优持股比例πS* 随着预期通胀波动率σA 与时间的关系
5 结语
本文基于Desmettre等[16]的研究框架,但区别在于Desmettre等[16]对高管薪酬的研究,而本文是在通胀环境下研究了高管的股权激励和工作努力最优策略问题。在研究方法上利用了伊藤公式来得到了高管的总体真实财富过程。
本文的研究表明:对数效用情形下,高管的最优持股比例未直接受到市场通胀风险增大的影响,但是高管的市场投资组合账户的财富比例因此而减小,从而间接影响到高管的总体财富的投资比例。幂函数情形下,职业水平较高的高管风险厌恶程度较低,而且采取的工作努力水平较高;但由于受到工作所产生的效用损失的约束,为了达到预期终端真实财富效用最大化的目标,高管需要做出权衡。当公司与高管执行长期的且包含股权激励的契约时,而且长期的共同利益诱导高管选择是看好公司的发展前景并做出最利于公司发展的行为,这种情形下市场通胀风险对高管的最优努力水平与最优持股比例几乎没有影响;当公司与高管执行包含股权激励的短期契约时,缺乏长远的共同利益诱导了高管的短视行为,所以当市场通胀风险变大时,高管减少努力并减小持股比例。本文结论对公司的股权激励理论做了有益的补充。

