双渠道风险传染下银行系统稳定性分析

姜闪闪，范 宏

（东华大学旭日工商管理学院，上海 200051）

1 引言

全球金融危机以来，银行系统的稳定性受到越来越多的关注［1］。特别是目前我国宏观经济形势复杂多变的情况下，研究银行投资收益波动、存款准备金率、储蓄波动以及储蓄利率波动的变化对银行系统稳定性的影响将变得尤其重要。而目前对银行系统性风险的研究大多是从银行同业拆借（直接传染渠道）的角度来分析金融系统的风险［2］。同业拆借市场为银行弥补流动性提供了便利，也为危机的蔓延提供了传染渠道［3］。银行同业拆借关系在银行系统的系统性风险中发挥着重要作用［4-6］。Kaufman［7］认为系统性风险是指银行间网络使整个系统崩溃的风险或可能。Mistrulli［8］的实证研究表明，银行间市场能够应对流动性冲击，但也通过银行间借贷充当银行倒闭的风险传播渠道。对于直接传染渠道的研究，目前主要集中在直接传染网络结构方面。Allen和Gale［9］研究了不同静态网络结构下银行系统的风险传染，发现银行间的风险传染很大程度上取决于市场结构，完全市场结构比不完全市场结构更稳健。Freixas等［10］发现，银行之间的联系越紧密，危机中单个银行的恢复速度越快，这结果与Allen［9］的结论类似。在银行网络的最优结构探索方面，Nier等［11］发现银行间的连接对系统性风险的影响不是单调的，并证实了最佳的银行网络结构应在风险分担和潜在的“多米诺崩溃”之间权衡［12］。在最初的时间，轻微地增加连接便增加了感染。当连接性增加到一定值时，连接性增加银行系统吸收冲击的能力，从而增加银行系统的稳定性。Kok［13］提出了一个连续的网络形成机制来研究关键参数如何影响银行间网络结构，并得到了与Nier等［11］一致的结论。Iori等［14］和Lenzu 和Tedeschi［15］研究了异构或同质银行节点情况下银行网络系统的稳定性。他们发现，当银行同质化时，银行网络更加稳定。Smerlak等［16］分析了系统性风险传染中单个银行的风险传染特征，发现大资本银行和低资本银行都能够增加系统性风险，这与Iori等［12］和Lenzu和Tedeschi［15］的 结 论 类 似。 另 外，唐 振 鹏［17］和 邓超［18］的研究表明在中心-边缘网络结构中系统重要性银行倒闭所造成的银行系统损失水平更高，但核心-边缘网络比其他结构网络表现出更强的恢复力，这个结论和Smerlak等［16］的结论一致。Caccioli等［19］研究了银行网络中的节点受到随机冲击和选择性冲击时，网络拓扑对系统性风险的影响。他们发现，无标度网络结构比随机网络结构具有更小的系统性风险。Han Jingti和Cao Yu［20］发现流动性囤积行为在早期减轻了系统性风险传染，而风险规避行为加剧了系统性风险传染。Steinbacher等［21］提出了一个基于网络的信用风险结构模型，以证明特殊和系统的冲击是如何在整个银行系统中传播。上述研究主要是从银行间市场（直接传染渠道）的角度来分析系统性风险，而很少考虑银行投资相关行为（间接传染渠道）对银行系统性风险的影响。

银行间的共同持有资产是金融风险传播的一个重要原因［22］。基于共同持有资产，Uhlig［23］研究了两种类型的金融危机。一种类型是银行由于外部冲击而重新分配其投资组合。在这种情况下，资产损失逐渐扩大使更多的银行资产处于危机之中，并导致金融危机。另一种类型是，一些银行将资产转移到了更安全的投资组合，导致一些资产价格下跌，导致一些银行陷入危机。Vries［24］做了类似Uhlig的研究。由于银行资产的相关性，银行资产分布的“胖尾”性质给银行带来了破产风险。Cifuentes等［25］和Greenwood 等［26］发现，在一个投资组合重叠的网络中，感染的风险主要来自资产价格的下降。Huang等［27］构建了银行资产双边网络模型，并利用2007年美国商业银行资产负债表数据对风险传染进行了实证研究，证实了共同持有资产对银行系统性风险有重要作用。Caccioli等［28-29］在共同持有资产的基础上，讨论了在杠杆率、市场拥挤、资产多元化和市场冲击条件下金融传染的可能性和程度。上述研究主要是从银行共同持有资产（间接传染渠道）的角度对系统性风险进行分析，并不能充分分析具有共同持有资产关系的银行间网络的演化规律。

上述的研究仍然存在一些问题：（1）上述模型考虑了银行间拆借（直接传染渠道）或银行共同持有资产（间接传染渠道）对银行系统性风险的作用，而不是同时考虑同业拆借和共同持有资产（双传染渠道）。Zhou Yichen和Li Honggang［30］从银行之间的债务联系和由投资组合重叠产生的联系出发，提出了一个复杂的网络系统，考虑了银行间借贷和共同持有资产。但在Zhou Yichen和Li Honggong［30］的研究中，银行同业拆借比例是确定的，资本资产比例是确定的，投资收益率和借贷策略不明确。（2）银行共同持有资产因素受宏观经济影响较大，特别是银行的投资收益率受到宏观经济形势的影响，具有趋势及互相关的性质。但是在上述单一渠道传染模型中，投资资产的收益率被设置为固定值，但实际上，投资是有风险的，投资收益率应该是动态的。基于以上分析，本文构建了一个双渠道的银行网络系统性风险传染模型。在该模型中，我们考虑了共同持有资产（间接传染渠道）和银行间借贷（直接传染渠道）的双渠道传染对系统性风险的影响，分析了系统性风险发生时银行共同持有资产和银行网络系统的演化规律。在模型中，银行可采用多种提高流动性的方法，包括银行间贷款和银行流动性低时的资产出售，资产出售时也考虑银行间互相持有的资产贬值。在所提出的模型中，受宏观经济波动的影响，银行持有的资产组合的平均收益率是动态变化的，是可以随经济景气状况的变化而变动。

2 双渠道风险传染模型

在银行体系中，银行破产往往是由于缺乏流动性造成的。银行的流动性与储蓄、投资和银行同业拆借息息相关。本文提出了一个能体现同业拆借和共同持有资产的双渠道风险传染模型，如图1所示，该模型能较好地反映银行系统的实际情况。

图1 具有共同持有资产的银行同业拆借市场结构

2.1 双渠道传染的动态银行网络系统

当银行缺乏流动性时，银行可以在银行间拆借市场进行借贷，如图1所示。在随机银行网络中，节点是随机连接的，连接矩阵表示为J，其中J ij为1或0。Jij=1表示银行i和银行j之间可能的信用联系，而Jij=0表示银行i和银行j之间没有拆借关系。银行i和银行j通过概率pij（0≤pij≤1）连接。

Nt是网络中的在时间t的银行数目，Nt是有界整数。动态银行网络以离散时间t=1，2，3，…，T进行演化。在时间t的银行i的流动性可以被描述为［12］：

其中（t）是银行i在投资、分红和借贷之前的流动性资产；Di（t）是银行i在时刻t的分红；Ii（t）是银行i在时刻t的投资；cij描述了银行i与银行j之间的连接关系，如果银行i与银行j存在借贷关系，cij（t）=1，否则cij（t）=0（c（t）不等于J，cij（t）表示银行i和银行j之间的实际贷款关系，而J ij表示银行i和银行j之间可能的信用联系）；Bij（t）＞0表示银行i从银行j借入的金额，Bij（t）＜0表示银行i贷款给银行j。

在时间t，每个银行的流动性都会发生变化，包括对存款人支付利息、投资、到期投资收益以及存款的波动。在时间t，银行在投资、分红和借贷前的流动性可以被描述为：

其中，Ai（t）表示时刻t银行i持有的存款，ra是银行存款利率，U i（t）是银行i的投资利润。在t时刻未投资的情况下，银行i所持有的全部投资资产如下：

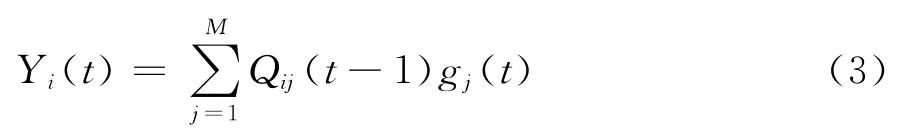
其中，Qij（t-1）是银行i在时间t-1持有的j资产的数量。Qij（t-1）是一个动态的变化值，因为银行i可能在每个时间步骤进行新的投资，并且资产的清算也可以在每个时间步骤实现。g j（t）是时间t的资产j的价格，可以描述如下：

其中δj（t）为在时间t上投资j的收益率，服从基于均值为τ的正态分布，即δj（t）∈N（τ，θ）。τ可以看是作所有投资的平均回报率，θ是资产价格的波动性。由于每个银行投资产品组合的不同，因此不同银行的平均投资收益率也不同。在时间步t，银行i将回收其投资资产的一部分，即U i（t）=p×Y i（t），其中p是投资回收的比例。投资回收后，继续投资前由银行i持有的全部投资资产为（t）=为投资回收后银行i持有的资产j的数量。因此，在分红和投资前的时间t银行i的所有者权益是：

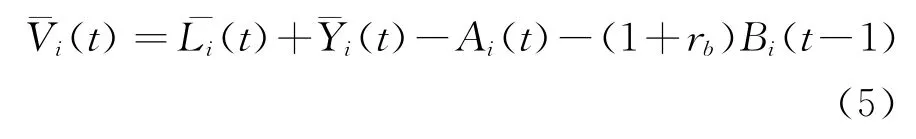
其中，Bi（t-1）是银行i在t-1时的银行间拆借负债，rb是银行同业拆借利率。在等式（1）中，银行i在时间t的分红D i（t）计算如下：

其中，χ是资本储蓄率，β是存款准备金率。银行发放股息的条件是（t）／Ai（t）≥χ。银行i的存款Ai（t）由以下方程决定［14］。

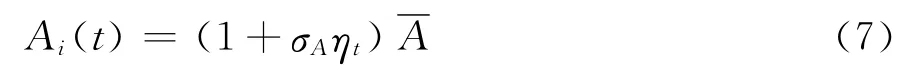
其中σA是所有银行随机存款的标准差，是所有银行存款的平均值，ηt∈N（0，1）。在t时刻未投资的情况下，银行i所持有的全部投资资产总数为Y i（t），而Ii（t）代表在t时刻银行i的新增投资。银行i在时间t的投资I i（t）可以由以下决定：

其中，ωi（t）是银行i在时间t的投资机会，其定义如下：

除了同业拆借外，本文中没有直接考虑银行贷款业务。在已有的大多数银行系统性风险模型中都没有将贷款业务直接考虑进模型，而是将贷款直接作为一种投资产品。本文中，重点考虑投资收益率的差别、同业拆借以及由于银行持有共同资产导致的风险传染。因此，本文中并没有考虑贷款业务的影响。

在上述银行系统中，银行出现以下破产情况：缺乏流动性、无法结清到期存款或债务。对于所有者权益大于0的银行，如果在分红和投资之后存在流动性过剩，那么该银行就是潜在的债权人银行，可以在银行间市场提供资金。而债务银行为了维持正常运作，需要从银行间市场借款。对于债务银行，如果从银行间市场借款足以偿还前一时期的借款，则偿还。与此同时，债务银行的流动性已经变为0。如果没有拆借到资金，或者借款不足以偿还最后一笔贷款和存款，债务银行将出售投资资产，直到它们能够偿还前一笔贷款和存款。如果出售资产不足以偿付先前的拆借，那么债务银行就破产，进行资产清算。资产必须首先用于偿还存款，其余的部分按比例偿还给债权人银行。

2.2 银行同业拆借中（直接传染渠道）的投资约束

在银行同业拆借过程中，同业拆借资金只能用于弥补短期流动性不足，而不是用于投资。对于流动性过剩的银行，等式（8）明确限制其投资金额，并且不能超过其现有的流动性资金。对于流动性不足的银行而言，只有通过银行间市场借入rb）cij（t-1）Bij（t-1）-（t）弥补流动性不足。rb是银行间同业拆借利率。投资约束下的银行同业拆借过程可以描述如下：

第一步：根据公式（2）计算银行i时间t的流动性（t）。如果银行i的流动性（t）为正，但银行i的债务B i（t-1）在时间t-1为负，那么银行i是暂时的潜在债权人银行。如果流动性（t）和负债Bi（t-1）同时为正，并且有（t）＞ （1+rb）Bi（t-1），则所有债务都已偿还，将流动性更新为（t）=（t）-（1+rb）Bi（t-1）。同时银行i成为一个临时的潜在债权银行。如果流动性不能偿还贷款，也就是说（t）＜ （1+rb）Bi（t-1），那么银行i是一个潜在的债务银行。

第二步：对于每个潜在的临时债权人银行，分红和投资按照等式（6）和等式（8）操作，并且流动资金更新为（t）-Di（t）-Ii（t）。

第三步：对于一个临时的潜在债权人银行i，如果（t）-βA i（t）＞0，那么银行i就是一个潜在的债权人银行，它可以将其流动性借给其他银行。但最大贷款额为（t）-βA i（t）。

第四步：在时间t，借方银行i一直从潜在的债权银行以随机顺序借金额B ij（Bij不可以超过债权银行j可以提供的贷款最高额度），直到银行i从其他潜在的债权银行借来的钱足够偿还以前银行同业贷款 （1+rb）Bi（t-1）。此时，债务银行i的贷款金额为 （1+rb）Bi（t-1）-（t），债务银行的流动性设置为：（t）=0。银行i的债务清偿后，债权银行j的流动性，更新为（t）=（t）+（1+rb）Bij（t-1）。如果银行i已经向所有潜在的债权银行申请贷款，但仍然无法借到足够的贷款偿还 （1+rb）Bij（t-1），那么银行随机出售资产Qij的直到满足还贷要求。如果出售资产仍无力偿还贷款，银行破产清算（资产必须先用于偿还存款，所有剩余的资产按比例返还给所有债权银行）。

2.3 共同持有资产（间接传染渠道）下的资产价格动态演化

当一家银行没有足够的流动性来偿还其债务时，它需要出售资产来偿还。如果出售的资产仍然不能偿还债务，银行将破产和清算。在上述过程中，抛售银行资产将导致资产价格下跌［31］。银行持有不同资产组合的网络如图（1）所示的双向图。假设网络中有N个金融机构和M个资产。每家银行根据等式（8）进行投资，银行i的资产组合为 ｛H i1，H i2，…，H iM｝（H ij=Qij（t）g j（t）），总 投 资 资 产 为H i=H i1+H i2+…+H iM。很显然，许多金融机构将同时投资于同一资产。不同的金融机构通过共同持有资产组合存在间接联系。资产价格的变化也影响着多个银行。一个银行资产的变化会通过共同持有资产影响其他银行。当银行流动性不足且不能贷款时，银行应出售资产以弥补流动性不足。此外，如果银行破产，破产银行将因资产清算而出售其资产组合，出售的资产将贬值。持有相同资产的银行会受到资产贬值的影响，导致所有者权益的损失，从而可能导致无力偿还债务，进而导致银行破产，进而进一步损害债权银行的资产。通过这种演进过程，银行间网络的初始冲击在系统中不断传播。在时间t，Qij（t）是银行i持有的资产j的数量，g j（t）是资产j的价格。当银行因缺乏流动性而出售其资产，或者一个银行因破产而清算时，资产将贬值出售［32，33］。在此，引入市场影响函数来反映资产价格的变化［28］：

在本文中，我们参考Caccioli的研究［28］，α取值为α=1.0536，即当资产的10%被出售时，资产的价格也降低了10%，这相当于对数价格的线性市场影响。在时间0时所有的价格设置为g j（0）=1。

3 仿真分析

整个银行网络系统随着时间t而演化，对于银行来说，其流动性资产、所有者权益和投资回报率（ROI）都随时间t而变化。在银行系统演化过程中，银行体系中的银行会由于不同的经营条件和经营策略而导致破产。由于银行系统性风险的存在，一个或几个银行的倒闭将导致系统中其他银行的连锁倒闭。银行网络系统在时间t的系统性风险是由网络系统的内部状态和内部参数决定的，而不是由银行网络系统的外部因素如存款利率、ROI等决定的。外部因素通过影响银行网络系统的内部变量而影响银行网络系统性风险。网络是随着储蓄利率ra、贷款利率rb、资本准备金率β、投资回报率δ等外部因素而演化的。为了有效地刻画银行的系统性风险，我们计算在［t+1，t+T］区间内破产银行平均数的归一化值Risk（t）。Risk（t）是系统性风险的计算值，可以表示如下：

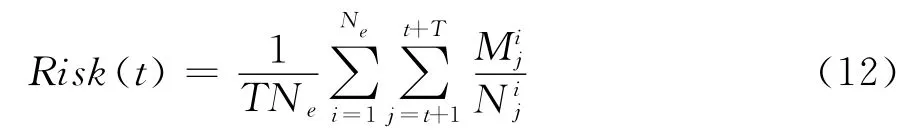
其中N e是重复仿真的次数，是在时间j网络中幸存银行的数量，是在第i次仿真中时间j时破产的银行数量。T是时间度，某一时刻的银行系统性风险表示为未来T时刻内银行倒闭的平均比例（平均累积风险），即未来T 时刻内银行倒闭的平均概率。在本研究中设置为T=200。目前有些研究是比较系统稳定后的结果，但也有很多研究除了比较稳定后的结果还比较银行演化的动态过程［14，28］。比较银行演化的动态过程可以看出银行系统中不同时刻的风险累积情况，因此本文将银行演化的动态过程的结果保留在对比结果中进行分析。公式（12）是系统整体风险的度量，不能区分直接风险传染和间接风险传染。本文中的系统性风险是由直接风险传染和间接风险传染共同作用的结果。

图2 存活银行的数量以及系统性风险大小随时间变化的曲线

在本研究中，使用了200个银行进行仿真（可以选择更多的银行进行仿真，但是200个银行已经充分地反应了银行网络的特性）。最大仿真时间步长是2000（在2000时间步长内，可以充分体现银行网络的动态特性）。银行可以投资的资产有150 种。每一次，每家银行都会随机收回35%的投资资产。在这项工作中，初始所有者权益服从均值为200的标准正态分布。平均投资回报率大于存款利率，即δ＞ra，这保证了银行系统具有利润率。利润率将影响银行系统的稳定性［34］。利润率越大，银行系统利润越多，银行运行越稳定。本文将资本储蓄率χ设定为30%，即股利必须满足银行的流动性超过储蓄的30%的条件。这种条件保证只有盈利的银行才能分红。我们考虑银行的约束行为，即银行的贷款不能用于投资，只能用于偿还贷款。

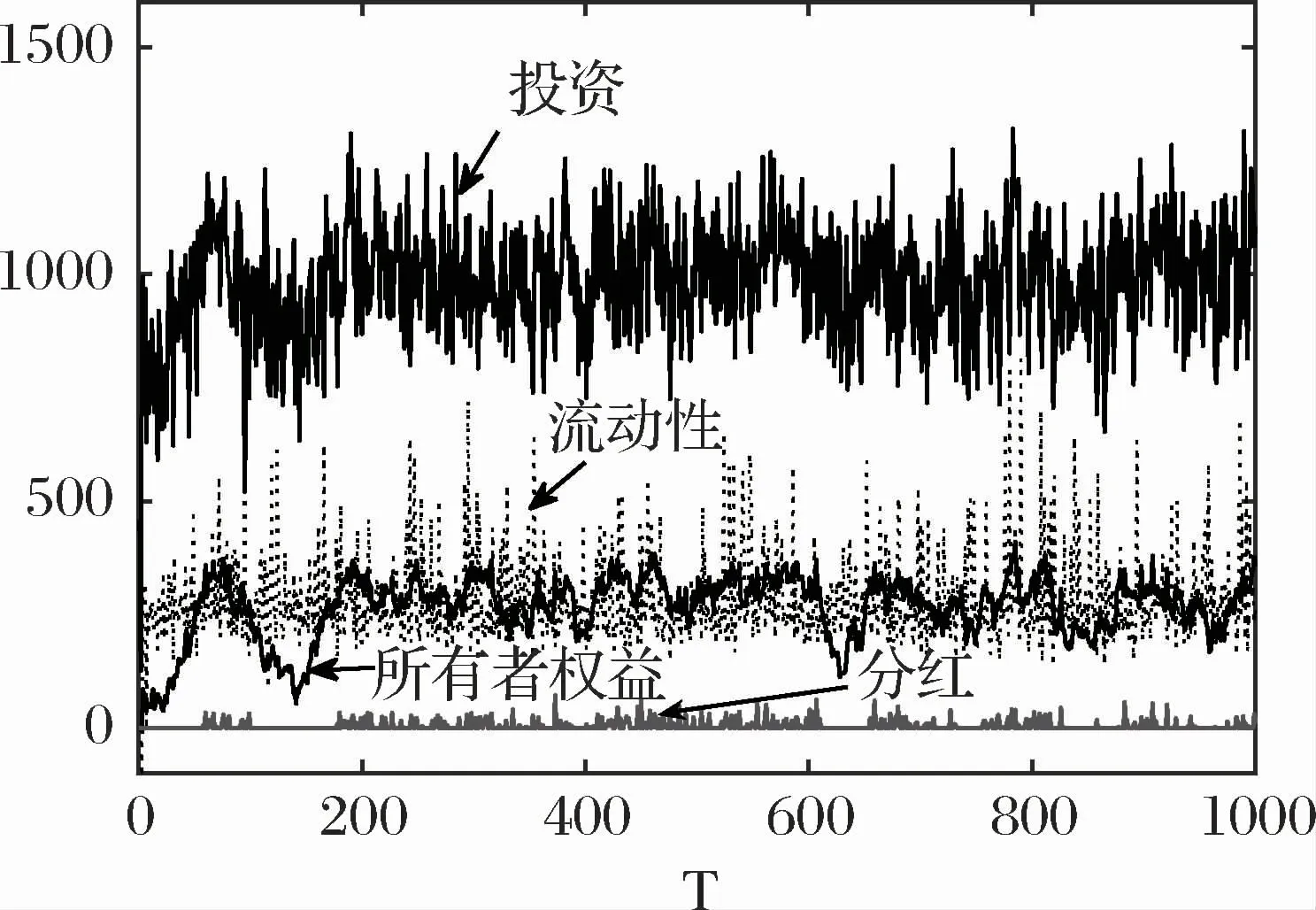
图3 某一典型银行的流动性资产、投资、分红以及所有者权益的演化

图2显示了银行网络中幸存银行数量的变化以及相应的系统性风险。图2表明，银行系统可能在第一步就崩溃，直到1000 步左右银行系统趋于稳定。网络演化初期系统性风险最大，这是由于不同银行系统初始状态不同造成的。银行初始资产净值服从均值为200 的正态分布。各银行的初始流动性、初始投资价值和投资方案是不同的。在实际的金融市场中，投资是有风险的，因此投资的回报率处于正常的分布。对于净资产低、流动性差的银行，如果投资收益率不够高，那么投资收益不足以支付储蓄利息和贷款，很容易破产。一方面，破产银行可能无法完全偿还银行同业拆借。另一方面，这些破产的银行会因为投资组合的重叠而使其他银行的资产贬值。这两个原因将导致银行破产的“多米诺”效应，并形成银行信贷风险的传染。当然，对于一家初始状态良好（净资产和流动性高）的银行，如果投资收益率较低，也会导致利润下降甚至亏损，最终破产。经过1000步，银行体系将趋于稳定，没有银行倒闭，这是因为银行系统消化了系统中的风险。在没有外部冲击的情况下，银行系统有足够的能力抵御资产价格波动。根据双渠道风险传染模型，可以得到银行的各种参数随时间的演化过程（如图3所示）。从图3可以看出，银行的投资、流动性、所有者权益以及分红都是一个动态变化的过程，是随着银行系统网络的内外因素的变化而变化的。

为了进一步验证所提出的模型有效性，本文从不同角度对模型进行了仿真：（1）不同ROI下系统性风险的演化过程；（2）平均储蓄规模、储蓄利率和储蓄波动强度对银行系统稳定性的影响；（3）银行准备金率对银行系统流动性和稳定性的影响。

3.1 投资收益率对银行系统稳定性的影响

银行的投资收益率与宏观经济形势密切相关，具有趋势及互相关的性质。图4给出了银行系统在不同的平均投资收益率下的变化。平均ROI越高，银行系统就越稳定。从图4 中可以看出，当平均ROI为0.008和0.009时，系统的风险在800步内可以变为0。当平均ROI为0.06和0.007时，银行网络中会一直存在系统性风险。这是因为平均ROI是储蓄利率支出和投资收益之间的余额过小，导致银行盈利能力下降，抗风险能力较弱。因此，平均ROI过低使得银行网络总是存在系统性风险。

图4 平均收益率ROI对系统稳定性的影响

3.2 存款准备金率对银行系统稳定性的影响

在不同的宏观经济条件下，监管部门会设定不同的存款准备金率。存款准备金率制约着银行资金的使用，对银行体系的稳定有着重要的影响。图5显示了银行系统在三种不同的银行准备金率下的变化。从图5可以看出，存款准备金率越低，银行破产的可能性就越小。当存款准备金提高时，可用于投资的资金数量减少，即投资的收入减少，但储蓄利息没有减少。因此，存款准备金率的提高降低了投资与存款之间的利润差，这将导致银行处理风险的能力减弱，并增加了信用违约的可能性。

3.3 储蓄相关因素对银行系统稳定性的影响

图5 存款准备金率对银行系统稳定性的影响

经济状况对民众的储蓄率有很大的影响，当宏观经济下滑时，由于经济期望的不明确，会导致储蓄率增加。相反，在宏观经济条件好转时，民众的消费等意愿的增加导致储蓄率下降。图6给出了不同平均存款量下银行系统的风险。从图6可以看出，平均储蓄量越大，银行系统越稳定。当平均储蓄量越大时，银行的资金就会变得更加的充裕，从而保证了充足的流动性，并且有更多的资金进行投资获取利润，提高了银行系统的稳定性，减少了银行倒闭的风险。

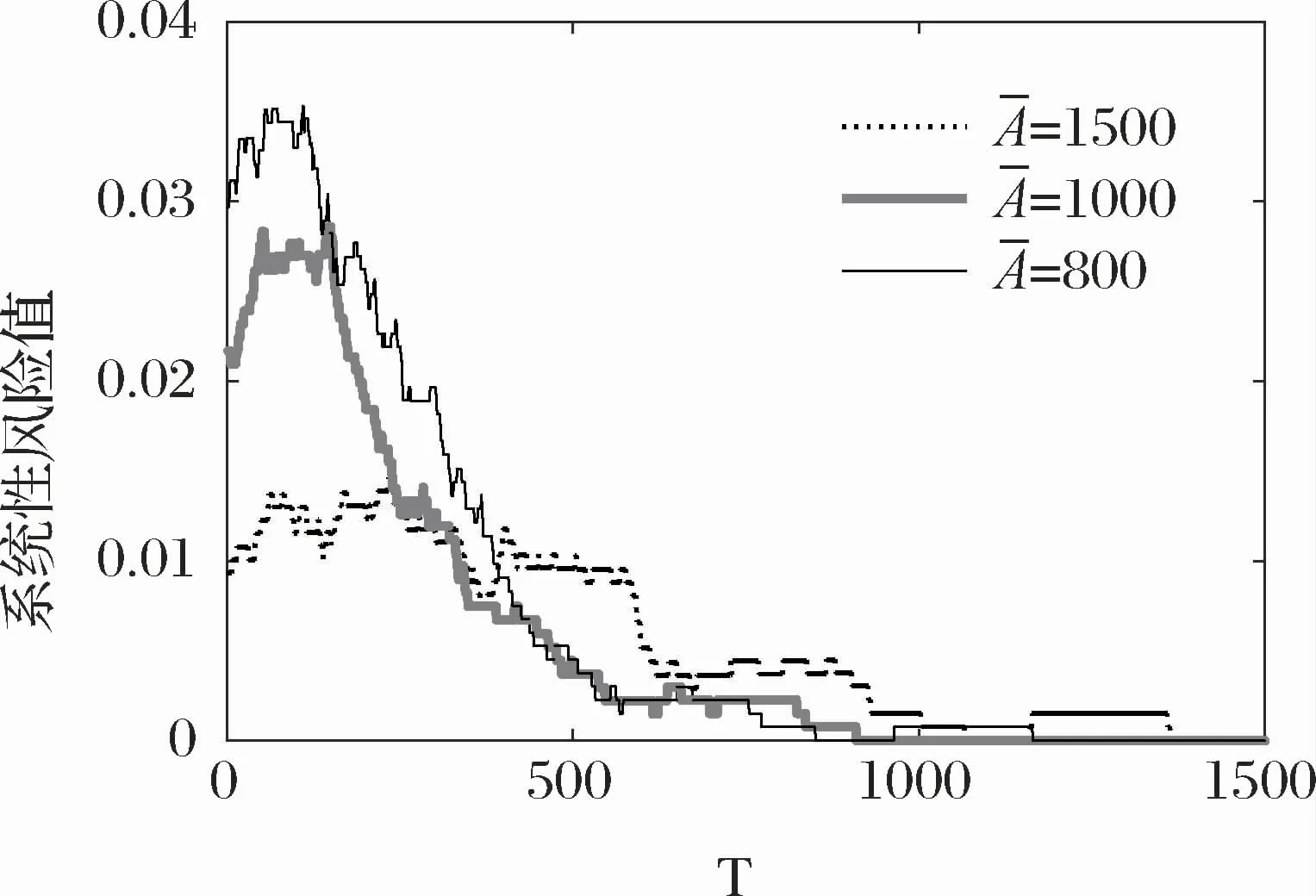
图6 平均存款量对银行系统稳定性的影响

另外，储蓄的波动幅度对银行系统稳定性也有较大影响。储蓄的波动幅度反映了不同银行吸引储蓄能力的大小。在经济趋势不好时，社会资金更加趋向存入资金规模大，经营状况健康的银行，从而导致不同银行的吸储能力的不同，从而导致储蓄的波动幅度变大，即σA变大。图7给出了不同储蓄的波动幅度下的银行系统性风险值。从图7中可以看出，储蓄的波动幅度σA越小，银行系统的风险越小。当储蓄的波动幅度变大时，会导致一些银行出现大的储蓄降幅，导致流动性变差，从而使得银行的风险增加。

一般情况下，经济趋势和利率具有负相关性。当经济趋势向好时，金融管理机构将有可能提高利率，紧缩货币供应，国家经济表现良好及利率的上升会增加该国货币的吸引力。当经济趋向负面时，金融管理机构将可能减息以刺激经济再度增长。因此，讨论储蓄利率对银行系统稳定性的影响可以反映经济状况对银行系统稳定性的影响。图8给出了不同储蓄利率下银行系统性风险的情况。从图8中可以看出，银行系统性风险和储蓄利率呈正相关。当储蓄利率为0.04和0.05时，银行系统最终可以稳定，系统性风险消失。当储蓄利率为0.06时，银行的系统性风险会一直存在。实际上，当储蓄利率过高时，银行的投资收益和储蓄利息支出之间的利差过小甚至为负，从而会导致银行的利润减少或亏损，最终引起流动性的不足。

图7 储蓄的波动幅度对银行系统稳定性的影响

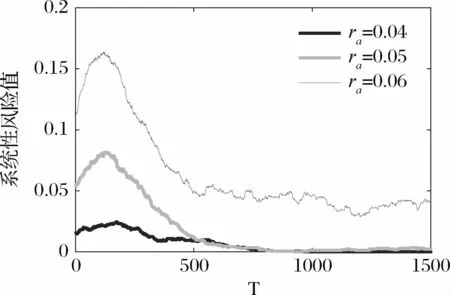
图8 储蓄的利率对银行系统稳定性的影响

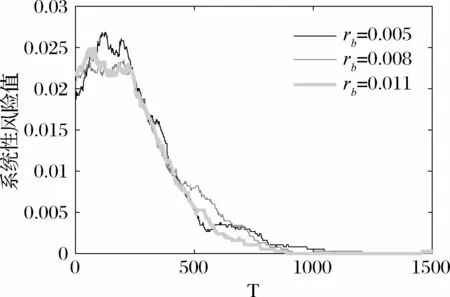
图9 银行间拆借利率对银行系统稳定性的影响

本工作进一步分析了银行间拆借利率对银行系统稳定性的影响，如图9所示。从图9可以看出银行间的拆借利率对银行系统稳定性几乎没有什么影响。在现实的金融市场中，往往银行间的短期拆借利率会非常高。1995年，俄罗斯金融市场资金短缺导致150 家银行无法履行提供资金的责任，隔夜拆借年利率达到200%-1000%。2016年，由于流动性不足，香港人民币隔夜银行间同业拆借利率（HIBOR）飙升至66.82%。但是拆借的高利率并没有对银行系统造成系统性风险，这是由于短期利息支出占银行的净资产的比例往往不高，可以通过银行利润来消化。从仿真结果可以得到下面一个有意思的结论：“能够借到钱才是最重要的”。

基于以上分析结果，本文尝试探讨不同经济形势下银行系统稳定的分析。事实上在经济形势较好时，银行系统较为稳定。这是由于经济形势较好时，银行可以得到较好的投资收益，银行的流动性较为充足，导致银行间的拆借相对容易。当经济形势转为负面时，适当降低银行的存款准备金率，实现流动性的增加，使得银行有充足的资金实现投资利润，从而提高银行的稳定性。另外，适当降低银行系统的储蓄利率也有利于提高银行的利润率。在经济形势较差时，资金规模较小，经营状况不够稳定的银行应当提高自身的吸储能力实现流动性的补足。另一方面，监管机构要在部分银行流动性不足时实施针对性的资本补足。

4 结语

研究银行投资收益波动、存款准备金率、储蓄波动以及储蓄利率波动的变化对银行系统稳定性的影响对银行决策者及监管部门有重要的意义。银行系统是由一系列银行及其相互关系构成的复杂网络系统。这种关联关系不仅与银行间市场有直接关系，而且与金融机构间同等资产的投资有间接关系。现有的研究要么集中于银行间市场，要么集中于银行投资的重叠组合，不能准确地对银行系统进行建模。此外，当前研究的一些假设是不实际的。例如，投资利率是固定的，流动性不能通过贬值来补充资产出售。由于研究假设的片面性和脱离现实性，以往的模型不能有效地反映银行系统的实际情况，导致现有模型不能有效反映的银行系统的演化过程。为了更好地反映银行体系的演化，本文提出了一种新的具有共同持有资产（间接传染渠道）和银行同业拆借（直接传染渠道）的双渠道风险传染模型。同时，由于经济系统受到各种复杂的经济形势影响，本文也考虑了各银行的投资具有投资风险，这对研究银行体系稳定性有着重要的影响。所提出的模型允许银行通过贬值出售资产来弥补流动性，这更符合银行系统的操作规则。研究结果表明，在经济波动情况下，平均储蓄量、储蓄的波动幅度、投资的收益率、存款准备金率以及储蓄利率等对银行系统稳定性的有较大影响。通过数值模拟，得出了一系列具有重要理论价值和管理意义的结论。

（1）ROI的平均值越大，银行体系就越稳定。如果平均ROI过小，存款利率和投资收益的差额就会趋于均值或负值，导致银行盈利能力下降，导致银行抵御风险的能力较弱，使得银行网络始终具有系统性风险；

（2）银行的稳定性对存款利率是敏感的，存款利率的变化对银行体系影响较大。存款利率越高，系统性风险越大；

（3）存款准备金率的提高降低了投资收益与存款利息之间的利润差，从而降低了银行应对风险的能力，增加了系统性风险；

（4）提高居民储蓄率，降低储蓄的波动幅度以及储蓄的利率可以有效的提高银行系统的稳定性。

该研究为定量研究动态银行网络系统的系统性风险问题提供了方案。但本文目前银行间的网络结构以及投资的网络结构都采用的随机网络，未来可进一步探讨不同网络结构下的银行系统稳定性，并可利用实际数据进行实证分析。另外，对新的银行的加入以及银行的贷款业务对银行系统性风险的影响的研究可以进一步完善本论文模型。