融入数学建模思想的线性代数案例教学研究
刘敬刚 郭燕


摘 要:针对线性代数课程传统教学方法中存在的不足,提出将数学建模思想融入线性代数案例教学过程的新思路.通过具体例子表明,在案例教学中贯穿数学建模思想,可以使抽象的线性代数理论、方法变得具体、形象、直观,加深学生对所学内容的理解,同时培养学生分析问题和解决问题的能力,提高学生的综合素质和创新能力,激发学生的学习兴趣,保证教学质量.
关键词:数学建模;线性代数;教学方法;案例教学
中图分类号:G642.0 文献标识码:A 文章编号:1673-260X(2020)01-0015-03
1 前言
线性代数作为理工科大学生的一门必修数学基础课,它在数学、物理、工程技术等方面具有广泛应用[1].随着计算机技术的日益普及和广泛应用,现代工程问题的解决最终都转化为线性代数方程组的求解问题,因此线性代数的理论和方法在大学生走上工作岗位后,有着十分广泛的应用.线性代数的核心内容是以矩阵为工具研究向量、向量空间、线性变换和线性方程组,这些内容比较抽象且理论性强,对于刚跨进大学校门的学生而言学习难度较大[2].同时由于线性代数课程设立之初,以介绍理论为主,教学实践中偏重自身理论体系的完备,强调定义、定理、性质等理论内容,而对线性代数的方法和具体应用不够重视,很少涉及具体应用实例,增加了大学生理解线性代数理论方法的难度.随着广大教育工作者通过线性代数课程的教学研究和教学改革,人们逐步认识到线性代数理论方法和实际应用相结合的重要性,但是在课堂教学中普遍存在以教师为主导的案例讲解仅仅说明线性代数有用,并没有让抽象的理论内容变得直观[3-5].当前“新工科”理念要求,课堂教学既能发挥教师的主导作用,又能充分体现学生的主体地位,实现课堂教学的“去中心化”[6].针对这种现状,本文提出将数学建模思想融入线性代数应用案例教学过程中,通过“教师引导、学生主导”重现问题分析、问题简化、建立模型、求解模型、结果解释和验证整个过程,让学生看到线性代数理论方法“有用”,同时培养学生应用所学知识分析、解决问题的能力,也为理解线性代数的抽象概念和方法提供有效途径.
2 数学建模思想融入案例教学的方法
面向实际问题,融合数学建模思想,依据线性代数有关理论建立数学模型,并应用线性代数方法进行求解,使原本抽象的理论、方法变得生动有趣,可以有效激发学生的求知欲,提高学习的积极性和学习效率.众所周知,数学建模的基本步骤为:分析问题、模型假设、符号说明、建立模型、求解模型、结果分析、模型检验等,下面以饮料配制问题为例介绍数学建模思想融入线性代数案例教学的设计方法.
例:饮料配制问题
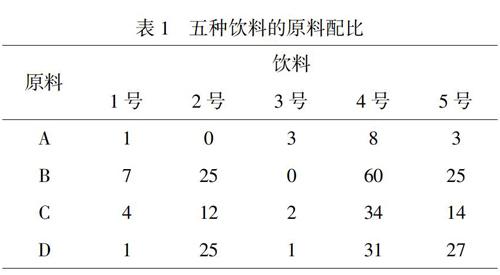
某饮料厂用原料A、B、C、D,按不同配比制成五种饮料(编号为1-5),具体原料配比见表1.某日,饮料厂第4号和第5号饮料售罄.问题:能否用其他饮料配制出这两种脱销的饮料?若可以,应该如何配制?
对于这样一个实际问题,一定会引起同学们的兴趣,可以极大地调动同学们对问题的探知欲望.依托数学建模思想,将数学建模基本步骤和线性代数理论方法有机结合在一起,具体分为七个步骤实现对问题的有效解决.为了叙述方便,首先考虑4号饮料的配制问题,5号饮料类似进行讨论.
1.问题分析
要配制出4号饮料,只需要讨论1、2、3号饮料,能否按某种比例混合后,满足4号饮料对四种原料的配比要求.
2.数据处理并提出具体问题
根据表1的数据,首先求出五种饮料在配比表中的列和,如表2所示.从而可以提出如下具体问题:假设要配制133单位的4号饮料,能否由1、2、3号饮料混合达到4号饮料的配比要求,如果能求出混合比例.
3.模型假设
假设原料可分.
4.符号说明
规定五种饮料在表2中的原料配比列和所示容量为一份饮料.设配制1份即133单位的4号饮料,需要饮料1、2、3分别为x1份、x2份、x3份.
5.模型建立
由已知信息建立如下数学模型
x1+3x3=87x1+25x2=604x1+12x2+2x3=34x1+25x2+x3=31 (1)
从而将4号饮料能否配制的问题,转化为非齐次线性方程组(1)是否有解的问题.
6.模型求解
由线性代数关于线性方程组解的存在性判定有关方法和结论,首先利用矩阵的初等行变换将线性方程组的增广矩阵化为行階梯形矩阵,
因为R(A)=R(A,b)=3,所以有唯一解,即4号饮料可以由1、2、3号饮料配制且配制方法唯一.
进一步,用初等行变换将增广矩阵化为行最简形,
解得x1=5,x2=1,x3=1.
7.结果解释
要配制133单位的4号饮料,分别需要1、2、3号饮料5份、1份、1份,即5份13单位的1号饮料、1份62单位的2号饮料、1份6单位的3号饮料混合可得133单位的4号饮料.
8.应用
综上,可知配制1单位的4号饮料,1、2、3号饮料分别需要,从而得1、2、3号饮料的混合比例为65:62:6.
以上过程针对4号饮料的配制问题,在数学建模思想指导下完成了对问题的求解.同理,假设要配制出一份即69单位的5号饮料,需要饮料1、2、3分别为y1份、y2份、y3份,建立如下数学模型
x1+3y3=37y1+25y2=254y1+12y2+2y3=14y1+25y2+y3=27 (4)
用矩阵初等行变换化增广矩阵为行阶梯形,可得
因为R(A) 饮料配制问题的求解过程中,教师用数学建模思想方法引导学生,应用线性方程组有关理论和方法分析问题、解决问题,突出了学生的主体地位.整个过程类似中学解应用题,大学一年级同学接受起来比较容易,但是其中蕴含着丰富的数学建模思想,具体有以下几个方面: 1.对问题进行分析,由已知数据信息求表1中原料配比的列和,丰富完善数据信息; 2.对问题进行必要的合理假设,即假设配料可分,该假设既符合实际又方便求解; 3.为了建模直观、方便起见,假设需要配制的饮料总量为1份,即表2所示饮料在原料配比表中的列和,从而得到简化的具体问题; 4.数学模型就是由赋予特定含义的数学符号,给出的数学表达式. 5.结果解释中,准确解释了的求解结果的具体含义,并且为了配制方便,将配比转化为在同一度量单位下饮料的混合比例. 依托数学建模思想方法,搭建了连接线性代数和实际问题的桥梁,将学和用自然结合、相辅相成,学为用作必要准备,用体现学的价值,充分调动了学生学习线性代数的积极性和主动性,提高了对线性代数理论方法的学习热情. 3 教学案例赋予抽象概念直观解释 线性代数中的向量、向量的线性表示、向量组的线性相关性和向量空间等概念比较抽象,当向量维数较高时没有相应的几何解释,给学习和理解有关定义、结论和方法造成了很大困扰.注意到饮料配制问题中五种饮料的配比都是有序数组,因此可以用向量来表示,记为 由(6)式可以看出,4号饮料能否由1、2、3号饮料配制的问题,就转化为向量?琢4能否由向量组?琢1,?琢2,?琢3线性表示的问题.换言之,就是?琢4是否属于?琢1,?琢2,?琢3生成的向量空间 又由于R(?琢1,?琢2,?琢3)=R(A)=3,所以向量组?琢1,?琢2,?琢3线性无关,是向量空间L(?琢1,?琢2,?琢3)的一组基.由问题(1)的求解结果可知?琢4可由向量组?琢1,?琢2,?琢3线性表,即?琢4∈L(?琢1,?琢2,?琢3),或者说?琢1,?琢2,?琢3,?琢4线性相关.同理分析可得,?琢5不能由向量组?琢1,?琢2,?琢3线性表,即?琢5?埸L(?琢1,?琢2,?琢3),或者说?琢1,?琢2,?琢3,?琢5线性无关. 总之,通过将饮料配制问题的数学模型写成向量形式,赋予向量、线性表示、线性相关性和向量空间等抽象概念具体的实际含义,对于抽象内容的学习和理解提供了帮助. 4 结论 在线性代数课程教学中开展融入数学建模思想的案例教学,有利于将线性代数理论方法和实际应用有机结合起来,有利于将线性代数知识的“学”和“用”有机结合起来,有利于将专业基础知识教育和学生综合素质、创新实践能力培养有机结合起来.通过案例教学,使线性代数理论方法在数学建模思想方法指导下成为解决实际问题的有效工具,不仅加强了学生对线性代数知识点的理解和掌握,更教给学生一种解决实际问题的方法,使学生养成良好的分析问题、解决问题习惯,掌握开启成功大门的钥匙. 参考文献: 〔1〕朱琳,蔣启芬.国外线性代数的教学研究述评[J].数学教育学报,2018,27(01):79-84. 〔2〕文军,屈龙江,易东云.线性代数课程教学案例建设研究[J].大学数学,2016,32(06):46-52. 〔3〕付传秀,周建新.线性代数教学改革中融入数学建模思想的探讨[J].教育教学论坛,2019(21):110-111. 〔4〕李清华.数学建模思想有效融入线性代数教学的探析[J].教育现代化,2018,5(39):77-79. 〔5〕段勇,黄廷祝.将数学建模思想融入线性代数课程教学[J].中国大学教学,2009(03):43-44. 〔6〕谢加良,朱荣坤,宾红华.新工科理念下线性代数课程教学设计探索[J].长春师范大学学报,2018, 37(04):131-133+138.

