时间尺度上奇异非保守Lagrange系统的Lie对称性和守恒量

陈志炜, 朱建青

(苏州科技大学 数理学院, 江苏 苏州 215009)

时间尺度理论在物理学、 控制系统、 力学和经济学等领域应用广泛.用对称性理论研究守恒量是分析力学的一个重要研究方向.文献[1]利用微分方程不变性的扩展群法得到了Lie对称性, 其主要思想为微分方程在无限小变换下的不变性; 文献[2]研究了Lagrange系统的Lie对称性, 得到了守恒量.目前, 对非奇异系统对称性和守恒量的研究已取得很多成果[3-8].在理论物理研究中, 由于量子色动力学、 量子味动力学、 电磁场、 相对论性运动的粒子、 杨-Mills场和超弦理论中的Lagrange函数均为奇异的, 因此对奇异系统的研究非常重要.文献[9]将相空间与位形空间中的Noether定理推广到时间尺度上；文献[10]研究了奇异Lagrange系统的Lie对称性和守恒量；文献[11]将Lie对称性推广到一类非完整奇异系统; 文献[12]将Hamilton正则方程的3种统一对称性推广到奇异系统, 即Mei对称性、 Noether对称性和Lie对称性；文献[13]研究了奇异非完整系统的对称性和守恒量；文献[14]分析了时滞奇异摄动控制系统的稳定性.文献[15]提出了时间尺度上的Noether定理；文献[16-17]研究了时间尺度上的Noether对称性和Lie对称性；文献[18]建立了时间尺度上Hamilton系统的Noether理论；文献[19]将Birkhoff系统的Noether对称性推广到时间尺度上；文献[20]研究了时间尺度上相空间中非保守非完整系统的Noether理论.但对时间尺度上奇异系统的对称性研究目前文献报道较少, 基于此, 本文将Lie对称性理论推广到时间尺度上奇异非保守Lagrange系统中.

1 时间尺度上系统的运动方程

假设力学系统的位形由n个广义坐标qs(s=1,2,…,n)确定, 其Lagrange函数为

L=L(t,qσ,qΔ),

(1)

所受非势广义力为

(2)

时间尺度上非保守Lagrange系统的运动方程为

(3)

若

(4)

则称该系统为时间尺度上的奇异系统.

求解系统中部分广义加速度, 记为

(5)

同时存在(n-r)个关系式:

βi(t,qσ,qΔ)=0,i=1,2,…,n-r.

(6)

2 确定方程和限制方程

取t和qs(s=1,2,…,n)的无限小变换:

(7)

其中：ε为无限小参数;ξ0和ξs为无限小生成元.生成元的向量形式为

(8)

其一次扩展为

(9)

二次扩展为

(10)

根据Lie对称性理论, 方程(5)在变换(7)下的不变性可表示为确定方程

(11)

将算子(10)代入式(11), 可得

(12)

方程(6)在变换(7)下的不变性可表示为如下限制方程:

X(1)(βj(t,qσ,qΔ))|βj=0=0,j=1,2,…,n-r.

(13)

定义1若无限小生成元ξ0,ξs满足式(12)和式(13), 则称该对称性为时间尺度上奇异非保守Lagrange系统的Lie对称性.

3 结构方程和守恒量

定理1若无限小生成元ξ0,ξs满足式(12)和式(13), 且存在G=G(t,qσ,qΔ)满足结构方程

(14)

则该系统存在守恒量

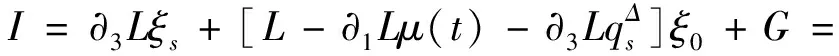
(15)

证明：

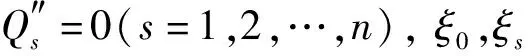
(16)

则系统存在守恒量式(15).

定理3若T=R, 则σ(t)=t,μ(t)=0, 根据式(14)可给出经典的奇异非保守Lagrange系统Lie对称性结构方程[10]为

(17)

由式(15)可得守恒量为

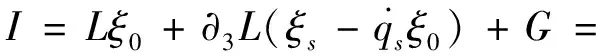
(18)

4 算 例

设T={2n:n∈N∪{0}}, Lagrange函数为

(19)

非势广义力为

(20)

1)建立运动微分方程.由式(3)给出

(21)

2)建立系统Lie对称性的确定方程和限制方程.由式(12),(13)给出

(22)

(23)

方程(22),(23)有解

ξ0=0,ξ1=1,ξ2=0.

(24)

3)建立系统的结构方程并求解G.对于式(24), 由方程(14)可得

GΔ=-1,

(25)

由方程(25)可得

G=-t.

(26)

4)求守恒量.由式(24),(26)及守恒量(15)给出

(27)

当T=R,σ(t)=t,μ(t)=0时, 系统的Lagrange函数为式(19), 非势广义力为式(20).由式(18), 经典的奇异非保守Lagrange系统守恒量为

(28)

综上, 本文基于微分方程在无限小变换下的不变性, 将时间尺度理论应用到奇异系统中, 给出了时间尺度上奇异系统存在Lie对称性守恒量的条件, 并得到了守恒量的具体形式.当T=R时, Lie守恒量的形式可将离散和连续系统统一.该方法和结果也可应用于时间尺度上其他系统的Lie对称性研究.