重叠和分组函数的分配性方程求解

吴 涛, 赵 彬

(陕西师范大学 数学与信息科学学院, 西安 710119)

1 预备知识

定义1[11]设LI={[x1,x2]|(x1,x2)∈[0,1]2,x1≤x2}, 规定[x1,x2]≤LI[y1,y2]⟺x1≤y1∧x2≤y2.

若x∈LI, 则记x1=l(x),x2=r(x), 即x=[x1,x2], 这里l(x),r(x)分别指x=[x1,x2]的第一个端点和第二个端点.易证(LI,≤LI)是完备格, 且0LI=[0,0], 1LI=[1,1].

定义2[18]U上的区间值模糊集是映射A:U→LI.

记U=[0,1]⊆,={[a,b]|0≤a≤b≤1}.

定义3[19]若二元函数O: [0,1]2→[0,1]满足交换性、 递增性、 连续性,O(x,y)=1当且仅当x=y=1,O(x,y)=0当且仅当x=0∨y=0, 则称O是重叠函数.

定义4[19]若二元函数G: [0,1]2→[0,1]满足交换性、 递增性、 连续性,G(x,y)=0当且仅当x=y=0,G(x,y)=1当且仅当x=1∨y=1, 则称G是分组函数.

定义5中的1,0分别是1LI=[1,1], 0LI=[0,0], 在不易混淆的情况下可简写为1,0.类似地, 可给出区间值分组函数的定义.由文献[11]中t-可表示三角模的定义, 下面给出可表示的区间值重叠函数的定义, 可表示的区间值分组函数的定义可类似给出.

定理1[16]设g: [0,1]→[0,1],h: [0,1]→[0,1]是两个单调递增的连续函数, 且g是严格的, 则如下两个条件等价:

1)(g,h)是重叠函数Og,h的乘法生成元对, 其中Og,h(x,y)=g(h(x)h(y));

2)h,g满足条件: ①h(x)=0⟺x=0; ②h(x)=1⟺x=1; ③g(x)=0⟺x=0; ④g(x)=1⟺x=1.

定理2[16]设s: [0,1]→[0,1],t: [0,1]→[0,1]是两个单调递减的连续函数, 且s是严格的, 则如下两个条件等价:

1)(s,t)是分组函数Gs,t的乘法生成元对, 其中Gs,t(x,y)=s(t(x)t(y));

2)t,s满足条件: ①t(x)=0⟺x=1; ②t(x)=1⟺x=0; ③s(x)=0⟺x=1; ④s(x)=1⟺x=0.

2 乘法Cauchy函数方程

定理3[2]设D是集合(0,1),[0,1),(0,1]或者[0,1], 则对连续函数f:D→, 下列两个条件等价:

1)对任意的x,y∈D,f满足乘法Cauchy函数方程f(xy)=f(x)f(y);

2)f=0或f=1, 或对任意的x∈D, 存在一常数c∈使得f(x)=xc.若0∈D, 则c>0.

引理1[7]设X={(x1,x2)∈[0,1]2|x1≤x2},f:X→[0,1]是一连续函数, 则下列两个条件等价:

1)对任意的(x1,x2),(y1,y2)∈X,f满足函数方程

f(x1·y1,x2·y2)=f(x1,x2)·f(y1,y2);

(1)

2)对任意的(x1,x2)∈X,f有下列5种形式：

①f=0;

②f=1;

存在唯一的c∈(0,∞), 使得:

存在唯一的c1,c2∈(0,∞), 使得：

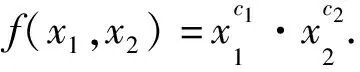
由引理1可得:

引理2设X*={(x1,x2)∈[0,1]2|x1≥x2},g:X*→[0,1]是一连续函数, 则下列两个条件等价:

1)对任意的(x1,x2),(y1,y2)∈X*,g满足函数方程

g(x1·y1,x2·y2)=g(x1,x2)·g(y1,y2);

(2)

2)对任意的(x1,x2)∈X*,g有下列5种形式：

①g=0;

②g=1;

存在唯一的c∈(0,∞), 使得:

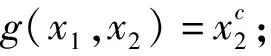
存在唯一的c1,c2∈(0,∞), 使得：

3 蕴涵算子基于可表示的重叠和分组函数的分配律

下面先给出经典情形下蕴涵算子基于重叠和分组函数分配性方程的解, 其中重叠和分组函数由乘法生成元对生成, 然后在推广的相应区间值下, 给出蕴涵算子基于可表示的重叠和分组函数分配性方程的解.

命题1设O: [0,1]2→[0,1]是由(g,h)严格乘法生成的重叠函数,G: [0,1]2→[0,1]是由(s,t)严格乘法生成的分组函数,I: [0,1]2→[0,1]是一个连续函数, 且满足对任意的z∈[0,1],I(0,z)=1, 则下列条件等价：

1)对任意的x,y,z∈[0,1], 三元组(O,G,I)满足

I(G(x,y),z)=O(I(x,z),I(y,z));

(3)

2)对任意固定的z∈[0,1],I(x,z)具有如下形式之一:

① 对任意的x∈[0,1],I(x,z)=1;

② 对任意的x∈[0,1], 存在一递减连续函数c(z)>0满足c(1)=0, 使得I(x,z)=g((s-1(x))c(z))=h-1((t(x))c(z)), 规定00=1.

证明: 1)⟹2).由已知O(x,y)=g(h(x)h(y)),G(x,y)=s(t(x)t(y)), 代入式(3)可得

I(s(t(x)t(y)),z)=g(h(I(x,z))h(I(y,z))).

(4)

令Iz(x)=I(x,z),u=t(x),v=t(y),fz=g-1∘Iz∘s,gz=h∘Iz∘t-1.由式(4)可得

fz(uv)=gz(u)gz(v).

(5)

由I满足I(0,z)=1可得

gz(1)=h∘Iz∘t-1(1)=h∘I(0,z)=h(1)=1.

于是可得fz=gz.从而对任意的u,v∈[0,1],fz(uv)=fz(u)fz(v).由定理3乘法Cauchy函数方程有fz=g-1∘Iz∘s=1, 化简得I(x,z)=1或fz(u)=uc(z), 即g-1∘Iz∘s(u)=uc(z), 化简得I(x,z)=g((s-1(x))c(z)), 再结合fz=gz, 则

I(x,z)=g((s-1(x))c(z))=h-1((t(x))c(z)),

由引理1知c(z)>0.

2)⟹1).

① 若I(x,z)=1, 则由重叠函数的定义可得I(G(x,y),z)=O(I(x,z),I(y,z)).

② 若I(x,z)=g((s-1(x))c(z))=h-1((t(x))c(z)), 则

命题2设Oi: [0,1]2→[0,1]是由(gi,hi)(i=1,2)严格乘法生成的重叠函数,I: [0,1]2→[0,1]是一个连续函数, 且满足对任意的x∈[0,1],I(x,1)=1, 则下列条件等价：

1)对任意的x,y,z∈[0,1], 三元组(O1,O2,I)满足

I(x,O1(y,z))=O2(I(x,y),I(x,z))；

(6)

2)对任意固定的x∈[0,1],I(x,y)具有下列形式之一:

① 对任意的y∈[0,1],I(x,y)=1;

证明: 1)⟹2).由已知O1(y,z)=g1(h1(y)h1(z)),O2(y,z)=g2(h2(y)h2(z)), 代入式(6)可得

I(x,g1(h1(y)h1(z)))=g2(h2(I(x,y))h2(I(x,z))).

(7)

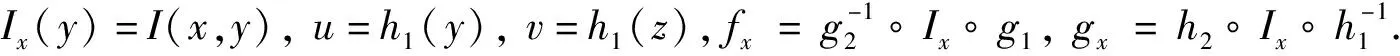
fx(uv)=gx(u)gx(v).

(8)

由I满足I(x,1)=1可得

由引理2知c(x)>0.

2)⟹1).

① 若I(x,y)=1, 由重叠函数的定义可得I(x,O1(y,z))=O2(I(x,y),I(x,z)).

1)令g1(x)=g2(x)=x,c(x)=x, 可得Yager模糊蕴涵I(x,y)=yx;

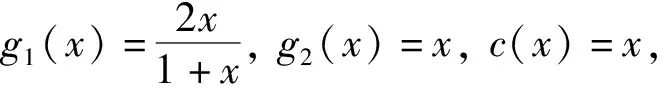
结合定理1和定理2易得以下结论: 若O1不恒等于O2, 则O1≤O2⟺g1≤g2∧h1≤h2.类似结论对分组函数也成立; 若G1不恒等于G2, 则G1≤G2⟺s1≤s2∧t1≥t2.下面考虑重叠函数和分组函数不恒相等的情形, 给出区间值模糊集中下列两类方程的解.规定00=1.

3.1 第一类方程

第一类方程为

(9)

式(9)可化简为

从而

对任意的固定的[z1,z2]∈LI, 记

式(10),(11)可化简为

由Oi(x1,y1)=gi(hi(x1)hi(y1)),Gi(x1,y1)=si(ti(x1)ti(y1))(i=1,2), 式(12)可化简为

令t1(x1)=u1,t2(x2)=u2,t1(y1)=v1,t2(y2)=v2, 有

令

其中u1,u2∈[0,1],u1≥u2.则

由

(14)

类似地,

(15)

其中

方程(14)的解分别有下列4种可能的情形：

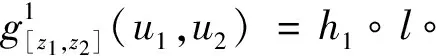
存在唯一的常值cz,dz∈(0,∞), 使得:

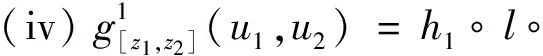
(18)

方程(15)的解有下列4种可能的情形：

存在唯一的常值ez,fz∈(0,∞), 使得:

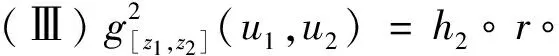
(19)

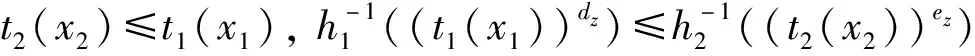
或存在唯一的常值cz,dz,ez,fz∈(0,∞), 使得:

(20)

由于

由于

3.2 第二类方程

第二类方程为

(21)

方程(21)可化简为

从而

对任意的固定的[x1,x2]∈LI, 记

(22)

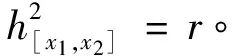
(23)

式(22),(23)可化简为

(24)

(25)

由Oi(y1,z1)=gi(hi(y1)hi(z1))(i=1,2,3,4), 式(24)可化简为

令h1(y1)=u1,h2(y2)=u2,h1(z1)=v1,h2(z2)=v2, 则

令

(26)

(27)

其中u1,u2∈[0,1],u1≤u2, 则

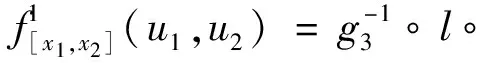
由于

(28)

类似地, 有

(29)

其中u1≤u2,v1≤v2,

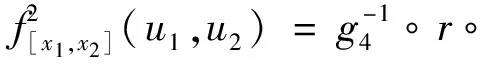
(30)

(31)

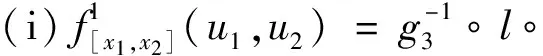
存在唯一的常值cx,dx∈(0,∞), 使得:

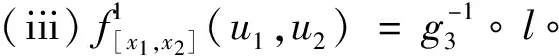
(32)

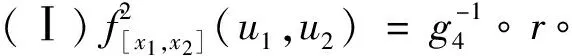
存在唯一的常值ex,fx∈(0,∞), 使得:

(33)

或存在唯一的常值cx,dx,ex,fx∈(0,∞), 使得:

4 重叠和分组函数之间的分配性

下面解决由Santos等[15]提出的关于重叠和分组函数分配性方程的问题: 是否存在不同于Omin的任意的幂等重叠函数O, 使得对单位元为 0 的任意的分组函数G对O可分配; 若不成立, 是否存在不同于Omin的一个幂等重叠函数O, 使得单位元为0的一个分组函数G对O可分配.类似的问题为对不同于Gmax的幂等分组函数G, 使得单位元为1的重叠函数O是否对G可分配.

定理4设O是不同于Omin的任意的幂等重叠函数,G是单位元为0的任意的分组函数.若G对O分配, 则这样的重叠函数O不存在.

证明: 假设存在一个不同于Omin的幂等重叠函数O, 对单位元为0的任意的分组函数G, 若G对O分配, 则

G(x,O(y,z))=O(G(x,y),G(x,z)).

(34)

以下所有的情形都成立:

若x=0, 代入式(34)得G(0,O(y,z))=O(y,z)=O(G(0,y),G(0,z)), 则式(34)成立.

情形1)若y=0∨z=0, 由式(34)的结构可知, 情形是对称的, 下面考虑y=0, 则

x=G(x,0)=G(x,O(0,z))=O(G(x,0),G(x,z))=O(x,G(x,z)),

其中x,z∈[0,1].

情形2)当x=0∨z=0∨x=1时, 式x=O(x,G(x,z))成立.当z=1时,x=O(x,1).若x≤y, 则x=O(x,x)≤O(x,y)≤O(x,1)=x, 即O(x,y)=min{x,y}.类似的结果对y≤x也有O(x,y)=min{x,y}.这与O不同于Omin矛盾.故这样的重叠函数O不存在.

定理5设O是不同于Omin的一个幂等重叠函数,G是单位元为0的一个分组函数.若G对O分配, 则这样的重叠函数O不存在.

证明: 假设存在一个不同于Omin的幂等重叠函数O, 由已知得G(x,O(y,z))=O(G(x,y),G(x,z)).取y=0, 化简得

x=G(x,0)=G(x,O(0,z))=O(G(x,0),G(x,z))=O(x,G(x,z)),

即x=O(x,G(x,z)).由分组函数G有单位元0, 有G(x,z)≥G(x,0)=x, 结合G是连续的, 引入记号mx,z=G(x,z), 且mx,z≥x,x=O(x,mx,z), 再结合O是交换的, 可知对任意的x,y∈[0,1],O(x,y)=min{x,y}.于是这样的重叠函数O不存在.

同理可得：

定理61)设G是不同于Gmax的任意的幂等分组函数,O是单位元为1的任意的重叠函数.若O对G分配, 则这样的分组函数G不存在.

2)设G是不同于Gmax的一个幂等分组函数,O是单位元为1的一个重叠函数.若O对G分配, 则这样的分组函数G不存在.

综上可见, 本文一方面给出了经典情形以及区间值模糊集中蕴涵算子关于重叠函数和分组函数的两类分配性方程的解, 所得结果可视为是蕴涵算子基于t-可表示的幂零三角模(三角余模)分配性方程的相关推广.另一方面, 本文否定解决了关于重叠和分组函数分配性方程的问题.