具有指数型二分性时标动力学方程的反周期解
孟 鑫, 吕 鑫
(1.吉林师范大学 数学学院, 吉林 四平 136000;2.四平市特种设备检验中心, 吉林 四平 136000)
1 引言与预备知识
时标理论[1]统一了离散与连续微积分, 使人们能更好地理解离散系统与连续系统之间的细微差别.近年来, 关于时标动力学方程解定性性质的研究得到广泛关注[2-5].反周期解是一类特殊的周期解, 关于微分方程和差分方程反周期解的研究已取得了许多结果[6-9].指数型二分性理论是研究微分方程和差分方程周期解的有力工具, 利用指数二分性理论可给出方程存在周期解的条件[10-11].本文主要研究非齐次线性时标动力学方程和半线性时标动力学方程反周期解的存在性.




|[h(σ(t))-h(s)]-hΔ(t)[σ(t)-s]|≤ε|σ(t)-s|,







xΔ(t)=F(t,x(t)),
(1)

xΔ(t)=A(t)x(t),
(2)

|Φ(t)PΦ-1(s)|≤K1e⊖α1(t,s),t≥s,
|Φ(t)(I-P)Φ-1(s)|≤K2e⊖α2(s,t),s≥t,
则称线性方程(2)具有指数型二分性.

Φ(t+ω)PΦ-1(s+ω)=Φ(t)PΦ-1(s),
Φ(t+ω)(I-P)Φ-1(s+ω)=Φ(t)(I-P)Φ-1(s).
2 主要结果
假设条件:
(H1)线性方程(2)关于投影P以及常数K1,K2,α1,α2>0满足指数型二分性;


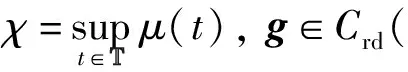
|g(t,x)-g(t,y)|≤L|x-y|,
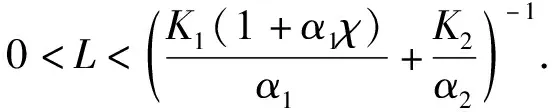
定理1假设条件(H1)~(H3)成立, 则非齐次线性方程
xΔ(t)=A(t)x(t)+f(t),
(3)
存在ω-反周期解x(t), 且
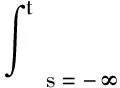
证明: 根据条件(H1), 可直接验证x(t)为方程(3)的解.根据条件(H3)及命题2, 有
故x(t)是方程(3)的ω-反周期解.
定理2假设条件(H1),(H2),(H4)成立, 则半线性方程
xΔ(t)=A(t)x(t)+g(t,x(t))
(4)
存在唯一的ω-反周期解.

考虑ω-反周期方程
xΔ(t)=A(t)x(t)+g(t,y(t)).
(5)
根据条件(H1)方程(5), 存在解
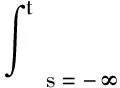

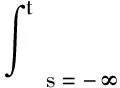
由于
故Ty∈X, 即T:X→X.
因为T:X→X, 所以T的不动点即为方程(4)的ω-反周期解.对任意的y1,y2∈X, 根据命题1, 有
因此,
从而T是X上的压缩映射, 根据Banach不动点定理, 映射T有唯一不动点, 即方程(4)存在唯一的ω-反周期解.

3 应用实例
例1考虑线性方程
(6)

当s≥t时, 有
因此, 若取K1=K2=4,α1=4,α2=2, 则线性方程(6)具有指数型二分性.
例2考虑非齐次线性方程
(7)


例3考虑半线性方程
(8)
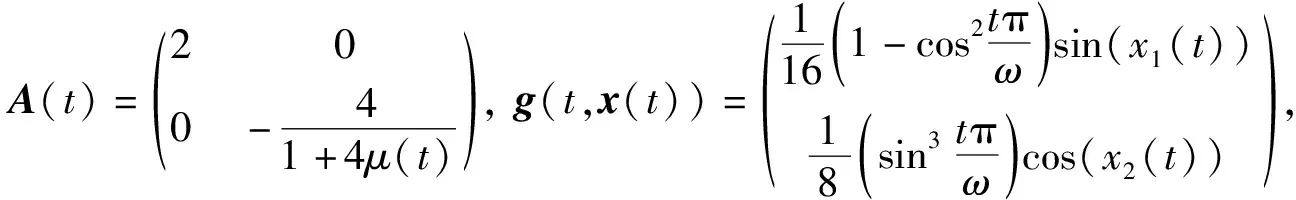

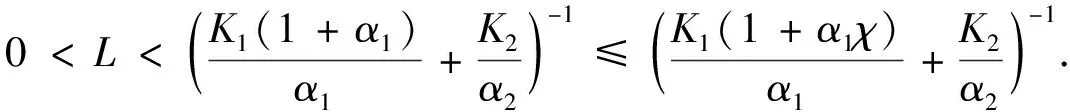
根据定理2, 方程(8)有唯一的ω-反周期解.

