分数阶不确定Like-Bao系统的有限时间同步

毛 北 行

(郑州航空工业管理学院 数学学院, 郑州 450015)

混沌分析及其同步控制目前已引起人们广泛关注[1-7].文献[8]研究了分数阶不确定Duffling混沌系统的终端滑模同步; 文献[9]基于适应转移函数滑模方法研究了分数阶Genesio-Tesi混沌系统的同步; 文献[10]用两种方法研究了分数阶Newton-Leipnik混沌系统滑模同步; 文献[11]研究了纠缠混沌系统的比例积分滑模同步; 文献[12]研究了一类复杂网络系统的有限时间函数投影同步; 文献[13]研究了时滞神经网络混沌系统的有限时间反馈同步; 文献[14]研究了一类神经网络混沌系统的有限时间同步; 文献[15]研究了分数阶超混沌Bao系统的比例积分滑模同步; 文献[16]研究了一类四维Like-Bao混沌系统的动力学分析; 文献[17]研究了超混沌Bao系统线性状态反馈控制及自适应控制.在此基础上, 本文研究分数阶不确定Like-Bao系统的有限时间同步, 根据分数阶有限时间同步理论给出Like-Bao系统达到有限时间同步的充分条件.

1 系统描述及主要结果

定义1[18]Caputo分数阶导数定义为

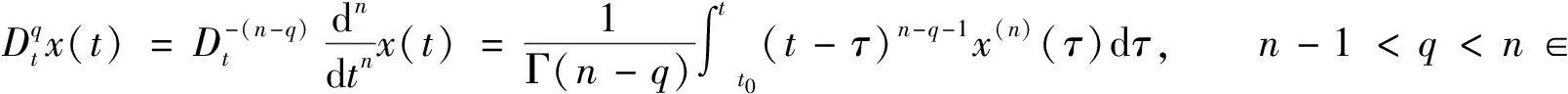
考虑Like-Bao混沌系统[16]

(1)

其中：a=38;b=6;c=20;k=2.该系统的4个Lyapunov指数分别为0.023 864,-2.895 738,-0.048 464,-6.085 664, 此时出现吸引子, 其轨迹相图如图1所示.

图1 系统(1)的轨迹

考虑分数阶Like-Bao系统

(2)

其中:a=38;b=6;c=20;k=2;q=0.927.该系统的4个Lyapunov指数分别为1.987,0.071,0,-18.058, 此时出现混沌吸引子, 分数阶Like-Bao系统的吸引子相图如图2所示.

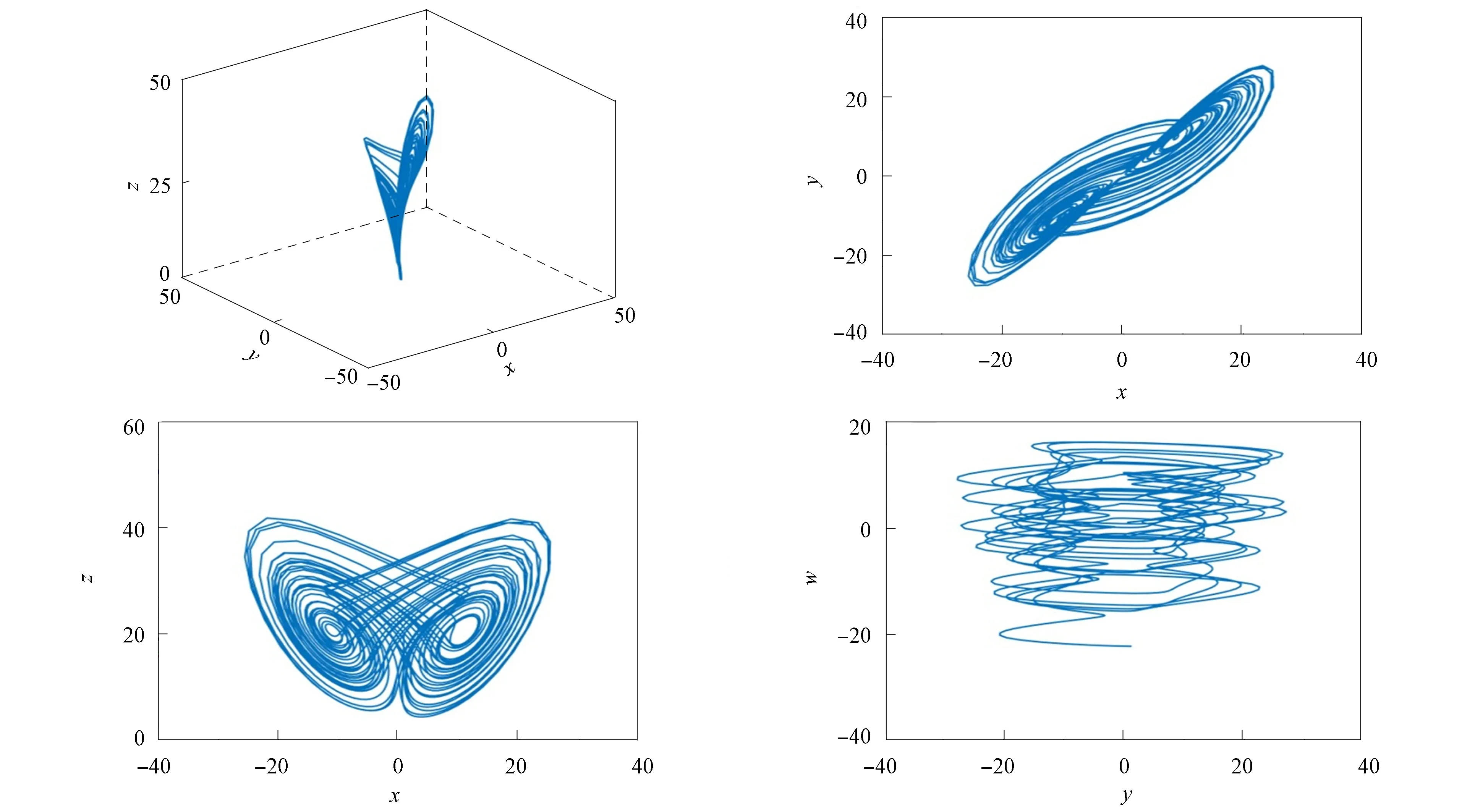
图2 系统(2)的吸引子相图

假设Like-Bao系统的主从系统均具有不确定性, 其主系统为

(3)

其中Δi(i=1,2,3,4)为未知参数或有界扰动, |Δi|≤ρi,ρi>0.Like-Bao系统的从系统为

(4)

其中Δj(j=5,6,7,8)为响应系统未知参数或有界扰动, |Δj|≤ρj,ρj>0.

定义e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω, 则有

(5)

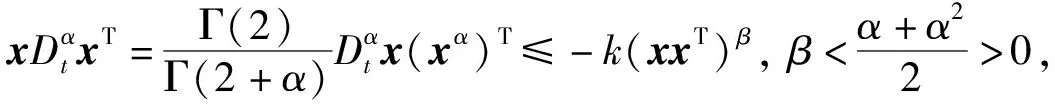
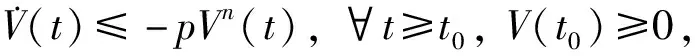
V1-η(t)≤V1-η(t0)-p(1-η)(t-t0),t0≤t≤T, 且V(t)=0,t≥T,

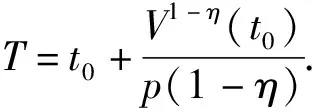
假设1γ1≥ρ1+ρ5,γ2≥ρ2+ρ6,γ3≥ρ3+ρ7,γ4≥ρ4+ρ8.

定理1在假设1条件下, 设计控制律:

则Like-Bao系统的主从系统(3)和(4)是有限时间同步的.其中:

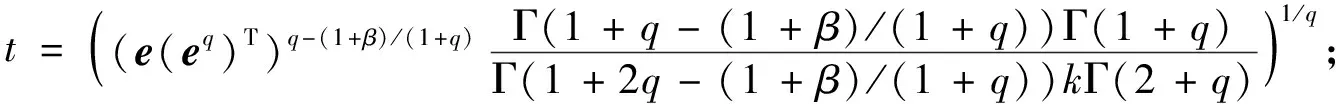
证明: 根据引理1可得

证毕.

作为分数阶系统的特例, 考虑不确定整数阶Like-Bao系统:

(6)

其中Δi(i=1,2,3)为未知参数或有界扰动, |Δi|≤ρi,ρi>0.以式(6)作为响应系统

(7)

其中Δj(j=4,5,6)为响应系统未知参数或有界扰动, |Δj|≤ρj,ρj>0.

定义e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω, 则

(8)

定理2在假设1的条件下, 设计控制律：

根据引理2可得结论.

2 数值仿真

下面采用预估校正法进行MATLAB仿真, 选取步长为0.01, 数值仿真时间T=20 s.a=38,b=6,c=20,k=2,q=0.927, 初值设为(x(0),y(0),z(0),ω(0))=(0.4,0.1,0.3,0.5),(x1(0),y1(0),z1(0),ω1(0))=(1.4,1.2,0.3,0.8),β=0.873,Δ1=0.2sint,Δ2=sint,Δ3=0.5cost,Δ4=cost,Δ5=sint,Δ6=0.5sint,Δ7=cost,Δ8=sint.控制增益γ1=2,γ2=2,γ3=2,γ4=2,ρ1=0.2,ρ2=1,ρ3=0.5,ρ4=1,ρ5=1,ρ6=0.5,ρ7=1,ρ8=1, 定理1和定理2的系统误差分别如图3和图4所示.由图3和图4可见, 初始时刻误差相差较大, 距离原点较远, 随着时间推移逐渐趋近原点, 且趋于一致.

图3 定理1的系统误差

图4 定理2的系统误差

综上, 本文研究了分数阶不确定Like-Bao系统的有限时间同步, 根据分数阶系统有限时间同步理论得到了对同步时间的估计.结果表明, Like-Bao混沌系统的驱动响应可在有限时间内取得同步, 且该结论可延伸至整数阶Like-Bao系统.