“依形解题” 优化计算

符强如

(新疆乌鲁木齐市实验学校，830026)

“数”与“形”是数学对象的两个方面,它们之间可以相互转化、相互解释、相互表征.本文就“依形解题”,优化计算进行探索.

一、 利用平面几何知识(添加适当辅助线)

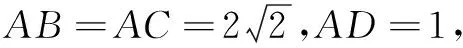
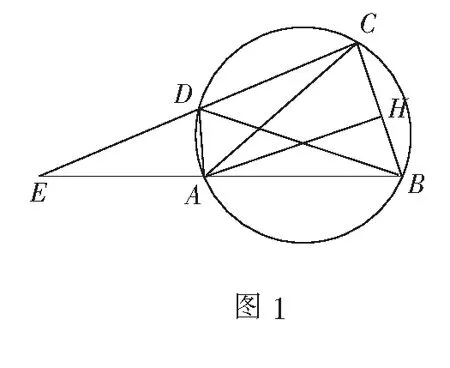
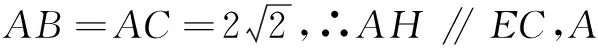
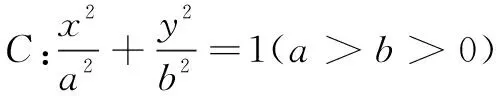
(1)求椭圆C的标准方程.

(2)过点F作与x轴不重合的直线l,l与椭圆交于A，B两点，点A在直线x=-4上的投影M与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.

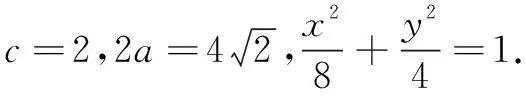
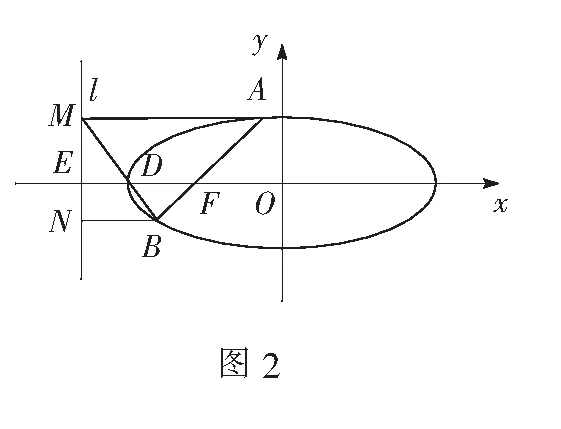
(2)如图2，设点B在直线x=-4上的投影为N,连结MN交x轴于E点.由椭圆第二定义可知直线x=-4为其左准线.设|AM|=m,|BN|=n.∴|AF|=em,|BF|=en.由题易知∆BFD∽∆BAM.

评注例1是典型的添加辅助线中位线,例2是利用平面几何知识(椭圆第二定义源于人教A版《普通高中课程标准实验教科书·数学(选修2-1)》第47页例6和第51页阅读材料).当题目中图形特征不易被发现时,可以通过添加辅助线或利用平面几何知识使其特征直观呈现,以“形”辅“数”,将问题等价转化,化抽象为具体,使问题解决有章可循,易于解决,优化了单一研究“数”的枯燥和繁琐的计算.

二、 利用定义和相关概念的几何意义

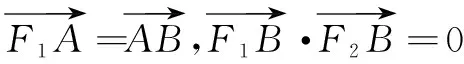
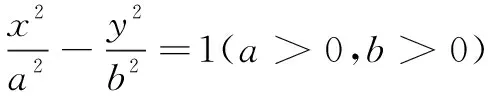
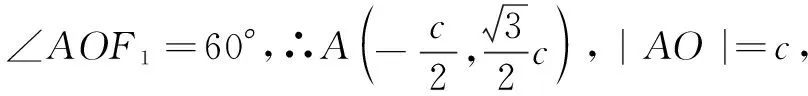
三、 利用平面向量相关知识

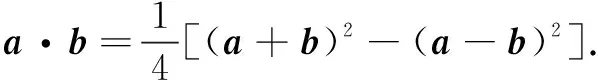
总之,对学生解题而言,需要下功夫的地方有化归方向、作图能力、数形转换等.教师需要引领学生发现问题的本质,努力使他们“想得到”,使复杂问题简单化，以“形”解题,以图形表现抽象代数符号,增加课程趣味性,降低学习难度,增强学习信心,提高学习效率，切实培养学生数学核心素养,落实“立德树人”根本任务.