“说数学”在新授课中的应用

徐春艳

(江苏省镇江中学,212002)

教学活动是师生双方共同参与的、积极的、互动的过程．课堂教学要有趣味性,要引导学生积极思考,让学生萌发创造性的思维[1]．为了实现这一目标,在高中阶段,要教会学生如何思考,注意思考的条理性,将思维和结果清晰地表达[2]．“说数学”是一种数学活动,它是通过语言将对某些数学问题的认识口头表达出来的一种活动．它可以是学生就某一个数学问题例如数学知识、数学心理和数学思维等来阐述自己对它的思考和理解,也可以是对数学概念、数学文化等表达自己所思所想,还可以是对一类问题的解法或规律进行总结．

本文以高中数学“平面向量基本定理”的新授课教学,谈谈如何通过“说数学”的活动让学生感受、体验知识发生、发展的过程,培养和提升学生的数学素养．

片断1设定情境 导入新课

问题1请你说说对向量共线定理的理解.

设计意图学习的最大动力是问题,有了问题就有了探究的欲望.可要求学生及时复习旧知识,提前预习新知识,新旧知识发生碰撞产生问题和困惑,带着疑问进课堂.问题会驱使学生追求真理,更加认真上课,积极参与课堂,在上课的过程中慢慢解开谜团,节约程序化学习的课堂时间.这里用提问的方式让学生回顾知识点,通过“说”，促进对新知识的学习．

片段2交流探究 建构模型

问题2是不是平面内的每一个向量都可以用某一个向量来表示?

问题3那怎样才能表示平面内的任意一个向量呢?大家一起来看两个物理问题,看看对你是否有启发？

情境1如图1，物体静止地放在斜面上,你能对物体所受重力进行分解吗?

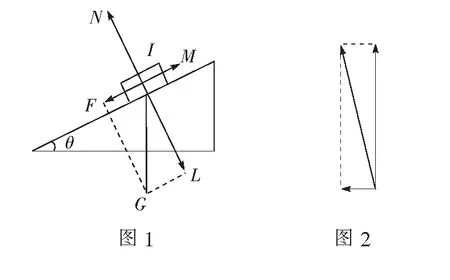
情境2如图2,火箭在空中高速飞行,你能对它的速度进行分解吗?

设计意图从学生熟悉的物理问题——力的分解、速度的分解来创设问题情境、提出问题,符合学生的认知规律．在教师的引导下，学生很快就能发现，这一物理问题本质上和要学习的向量分解是一回事,学生动手画出直观的图形,说出问题的解法,在同伴中成果分享,很好地激发学生学习的热情.在此过程中，可引导学生能在潜意识里使用平行四边形法则,为后面引出向量的分解做好铺垫．

片断3启发生疑 激发火花

上节课学习了向量共线定理的相关内容,那么对于确定的向量e1和e2(不共线),“任一向量a”的这种分解是否成立?如果成立,对于不共线向量e1和e2，在a=λ1e1+λe2中，实数λ1,λ2是否唯一？

这个问题的发现是本节课的难点,学生比较难以理解,但是作为教师也不能直接给出答案,否则就是剥夺了学生思考的权利,不利于数学核心素养的养成.所以,这里需要教师做一个引导者,通过师生对话,类比讨论,让学生拨开云雾见太阳．对于学习的每个环节所遇到的困惑,分组合作,通过与同伴交流,互相借鉴,共同面对.教师观察引导,各组做完派代表汇报,学生自我反思,互相切磋,说说自己解决问题的方法和步骤,促进数学核心素养的养成．

设计意图通过前几个问题的设置和解决,引申出一个向量如何用其它向量来表示的问题, 自然会产生困惑,自然会类比向量共线定理.引导学生自己主动去类比、观察、归纳 、分析、概括，最终解决问题,同时培养学生的直观想象和数学抽象素养．

片断4概念辨析 深化理解

请同学们勾画出概念中的关键词,并思考几个问题:

(1)e1,e2满足怎样的条件才可以作基底?

(2)基底e1,e2唯一吗?

(3)定理中的实数λ1,λ2唯一吗?

(4)平面向量基本定理的本质是什么?

将图形语言转换成文字语言,培养了学生抽象、概括、归纳的能力,提升了学生的数学抽象素养;通过教师启发、点拨、有效的师生对话、生生对话,互相补充,完善定理内容,深入理解平面向量基本定理．让学习共同体之间互相“说”,进行合作探究,让学生懂得平面内任一向量都能用两个不共线向量来线性表示,体验到了由特殊到一般的过程,强化了学生直观想象和数学抽象素养．

设计意图在给出以上问题之前,可引导学生首先通过思考交流，构建概念,经过讨论并归纳“画”出平面向量基本定理的内容对应的图形语言,然后在教师的引导下，将图形语言转化为文字语言，得到平面向量基本定理的内容．教师继续点拨,通过设计问题串让同学来说,加深学生对概念的理解．

片断5典例精析 应用升华

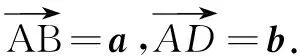
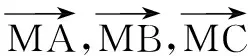
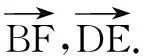
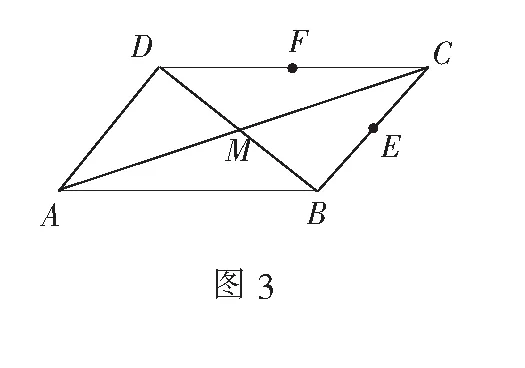
在讨论过程中,学生之间互相“揭短”,有学生说表示向量就是要找三角形,再用三角形法则,加加减减;也有学生说表示向量还可以找平行四边形,利用平行四边形法则;还有学生说前面同学说的其实都是几何方法,还可以是用代数方法,化归为向量共线定理求系数,用待定系数法求系数．

设计意图让学生在讨论中自由发挥,让大家一起参与“说”,整个过程集大家的智慧来总结向量表示的方法．

成功的数学教学，不仅让学生会“做数学”,还要让学生会“说数学”,这就需要学生会独立自主地去使用已经掌握的知识,并创造性地去探索新知识,掌握一些常见的数学思想和基本方法,学会提出问题， 思考问题，解决问题．教师要注重学生核心素养的培养和提升,数学核心素养的培养并非一朝一夕的事,需要努力为学生搭建“说数学”的平台.通过“说”的过程不断思考、推理,训练他们的思维,提高学生的表达能力；鼓励学生在知识的学习中互相质疑,感到迷惑时提出疑问,有遗漏疏忽的地方相互补充.在“说数学”的过程中师生、生生互相启发,实现教学相长．