关注教学细节 助力深度学习
刘 鹏
(江苏省锡山高级中学,214174)
所谓深度学习是相对于浅层学习而言的,浅层学习是一种无关联、孤立的学习,其关注点是数量,是学时的长短;而深度学习提倡主动的、在理解基础上的学习,它要求学生主动地将新、旧知识加以关联,达到更高的思维层次,其关注点是质;其次深度学习更关注学生的过程性思考与知识体系自主建构,其评价指标更倾向于能力等.
本文就教师如何关注教学细节,助力学生深度学习方面和广大同仁共同探讨.
一、有备而来,让学生倾心投入深度学习
学生能够快速进入深度学习状态,需要两方面的准备.首先是思想上的准备,其次是基础知识上的准备.学生只有对所学内容感兴趣,思想上愿意参与问题的思考和解决,才能积极主动进入学习状态.教师在备课时,分析学生与教材,设计符合“自己学生”的教学计划、教学手段,使其注意力尽快集中于教学内容,精神快速进入“亢奋”状态.因此教师在课前就有必要和义务为学生介绍、创设主题的背景知识,或提供与教学内容相关的材料,让学生也有备而来,为全情参与教学活动,为深度学习做好思想和知识的准备.
案例1在(苏教版2-1)“导数—平均变化率”教学时,结合学生在高一《数学》必修2中已经学习直线的斜率和物理中已学习加速度等知识储备,教师可根据学生的年龄特征,在课前设置一小段游乐场中的过山车视频,过山车的上下穿梭,游客的尖叫可快速将学生的注意力引入课堂,精心设问:“为什么在相同的时间里,游客的感受差异如此巨大?”“如何用数学语言描述这一变化特征?”等等,将学生的思维引向主题.
二、精心设问,让学生在问题探究中深度学习
问题是实现课堂教学目的的重要手段,是引领学生快速进入深层学习的阶梯和推进剂.因此,教师应该结合教学目标、教学的重点、难点精心设置问题,让学生在问题解决的过程中进行新、旧知识的类比、衔接,从而实现学生知识、方法体系的重新建构,思维能力的提升,达成深度学习的目标.
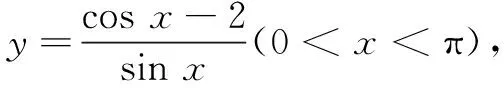
本题是三角函数与分式函数的复合,初次接触本题,大部分学生会感到束手无策.究其原因有以下几点:一是函数最值的求解方法单一;二是基本概念、公式不熟悉;三是数形结合意识不强,转化能力弱.故此时设置适当的问题串,有助于明确方向,拓展思路,激发兴趣,助力问题解决和能力的提升.如设置如下问题串:
(1)求函数最值有哪些方法?要注意些什么?
(2)你能判断此函数的单调性吗?有哪些方法?
(3)能否“数形结合”解决此问题?
(4)可否转换角度利用三角函数的有界性解决?
问题(1)有利于学生对求函数最值常规方法的回顾、汇总,有利于激发学生的探究欲望;问题(2)指出求解最值问题的常规方法—利用函数的单调性,而单调性的判断又可以考虑定义法、导数法和复合函数的单调性,本题以导数法判断比较理想;问题(3)对学生思维提出新的挑战,将函数值看作点(sinx,cosx)和点(0,2)连线的斜率,结合动点轨迹,数形结合来求y的最大值;问题(4)再次激起学生思维的跨越,用y表示sin(x+φ),利用三角函数的有界性求y的最大值.
三、留足时间、空间,让学生在“剥茧抽丝”中深度学习
每节课(特别是起始课、概念课)都有其确定的重点和难点,如何化解这些重点和难点,有的教师为了“节省时间”,往往是直接给出定义、结论,再辅以大量练习来实现目标,其短期效果较好.故教师在课堂上要适时、大胆留足时间和空间,让学生参与知识发生、发展,相信只有亲身经历才会理解得更加深刻,运用得更加自然.
案例3“函数的单调性”(苏教版必修1),其教学难点是如何得到函数单调性概念的形式化定义以及对定义中“任意”、“都有”的理解.学生在初中已经学习了正比例函数、一次函数、二次函数和反比例函数,应该说对函数的增减性有一定的感性认识,教师再出示函数y=2x,y=-2x的图象,绝大部分学生都能结合函数图象用自然语言说出函数值y随自变量x的值变化而变化的情况.随后教师提出如下的问题让学生展开讨论:不看图象,仅根据“0<1时,f(0) (1)判断函数在区间(0,+∞)上的单调性; (2)判断函数在各自定义域上的单调性. 通过对重点、难点的全程参与和解决,学生真正理解定义中的“任意”、“都有”的含义和单调区间的意义.相信大部分学生对函数单调性的概念内涵和外延的理解会更加深刻,对如何研究新问题有了新的理解. 在日常教学活动中,教师总免不了对学生的表现给予评价,但不同的评价方式产生的教学效果差异是显而易见的.一方面,中肯、激励性的评价让学生备受鼓舞,促使学生再接再厉,忘我投入,敷衍、嘲讽、批判性的评价让学生意志消沉,心生厌恶.另一方面,评价要丰富、全面.可师生互评,也可同学互评;不仅要对结果的正误做出评价,还要对其解题过程或其它方面作出评价;对正确的、独特的展示,要进行肯定和表扬,对错误的、有缺陷的展示要指出问题所在,同时还要挖掘其闪光点. 在充分思考后,学生甲举手说出其解法如下: 教师进一步补充点评“我也同意生乙的观点,同时我还很欣赏甲同学的主动、清晰和有条理的表达,希望大家都要向他学习.”,又问生乙有何方法?生乙说“想用建立直角坐标系的方法解决,但感觉可能不行,因为要引入多个字母.”教师首先说:“其实我也有这种想法,因为建立直角坐标系是一种常用方法,它可以降低思维难度,且其普适性也较强.那如何建系呢?”学生乙说明具体建系方法,师生一起得出: (-a-x)2+(-y)2=32, (a-x)2+(-y)2=22, 两式相减得4ax=5,所以 至此,教师本想结束本题,突然看到平时数学基础不是很好,又不怎么说话的同学丙似有话要说,旁边的同学也跃跃欲试,教师马上说:“下面我们一起来欣赏丙同学的想法.” 教师还未说话,同学们便一起鼓掌,学生丙也面露羞涩、兴奋之形.教师也跟着鼓掌,点评“很好!此种方法适合填空、选择题,抓住任意性,化一般为特殊,体现出丙同学思维的灵活性.希望下次能主动、大胆表达自己想法.” 《普通高中数学课程标准》明确要求,“体现数学的文化价值”要作为高中数学课程的基本理念之一.在数学课堂上要尽可能多地宣传、展示身边的数学,生活中的数学,数学家的轶事,主动展示数学美,让学生发现、感受数学美——数学图形的对称美、奇异美,代数式的形式美、结构美和问题解决的逻辑美等等.这样学生才能“长”出发现美的眼睛,喜欢数学,爱上数学,深度学习数学自然水到渠成. 特别在一些章节的起始课、总结课中,教师要重视数学内容的人文教育,美育教育,不可一带而过,错失教育良机.如在学习圆锥曲线的起始课时,教师可以展示一些学生熟悉的和椭圆、圆、双曲线和抛物线有关的器物,“神州”系列卫星的运行轨道等图片,还可以介绍一些椭圆、抛物线、双曲线性质在现代医学、汽车制造等行业中的运用例子,以此激发学生学习圆锥曲线的兴趣,让其体会圆锥曲线就在我们身边.又如在学习数列时,可以适时介绍数学史上的几大猜想以及我国著名数学家陈景润在此方面的贡献和相应趣事,让学生感受数学家的献身精神和百折不挠的意志品质,感受数学的神奇魅力,增强民族自豪感.再如说到“数形结合”时,可介绍华罗庚教授为强调这一方法重要性时写的一首词:“数与形,本是相倚依,焉能分作两边飞;数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休,切莫忘,几何代数统一体,永远联系莫分离.”让学生领略到数学家的多才多艺、温情可爱的一面,同时通过这样的介绍也有利于增强学生对这些知识、方法的深刻理解,有助于学生主动进行深度学习.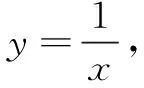
四、评价全面、中肯,让学生乐于深度学习





五、加强人文和美育教育,让学生在“欣赏”中深度学习

