“函数的零点”教学实录与思考

黄 荣

(江苏省无锡市第一中学,214031)

近日,观摩了一节公开课，课题为“函数的零点”,取得了预期的教学效果.本文展示这节课的教学实录,并谈谈笔者的几点思考.

一、教学实录

1.零点概念

学生自主阅读学习苏教版《数学》必修1教材91页到92页例1之前的内容(4分钟).

师:什么是零点?

生:对于函数y=f(x),使f(x)=0的实数x.

师:如何从数和形两个角度理解函数的零点?

生:从数的角度看,函数y=f(x)的零点为方程f(x)=0的根;从形的角度看,函数y=f(x)的零点为函数y=f(x)图象与x轴交点的横坐标.

教师PPT展示函数零点、方程根、函数图象与与x轴交点横坐标三者的关系.

例1如图1，说出函数y=f(x)的所有零点.

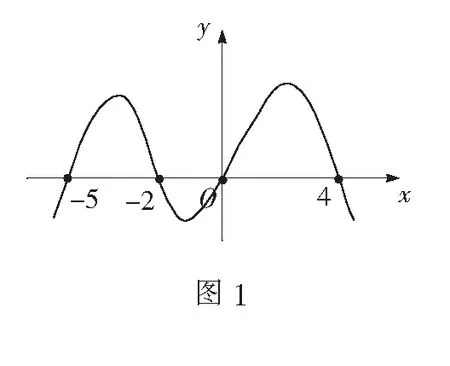
生:-5,-2,0,4.

师:零点本质是实数,而不是点,如-5不能说成(-5,0).

2.零点探求

思考1:请你设计一个判断一次函数f(x)在区间(a,b)上存在零点的方法.

生:f(a)·f(b)<0.

思考2:你设计的方法能否推广到任意函数,说说你的看法.

生:不能,要求函数f(x)在区间[a,b]上的图象是不间断的.

思考3:请同学们改进方案,组织语言,并形成定理.

学生经过思考、讨论,归纳出零点存在性定理:若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)上有零点.

3.定理探究

探究1怎么理解定理中的“有”?

生:“有”,即存在,表示至少有一个零点.

追问①:零点个数有规律吗?

生:有奇数个零点.

师:一定是奇数个?有没有反例?

两位学生在黑板上画出反例,如图2所示.

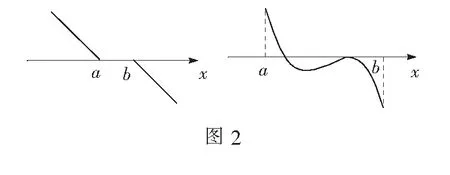
追问②:若f(x)是二次函数,有几个零点?

生:在区间(a,b)上只有唯一零点.

追问③:对于一般函数能否增加一个条件,使零点唯一?

学生:函数y=f(x)在区间(a,b)上单调.

探究2图象不间断.

① 若f(a)·f(b)>0,函数f(x)是否一定不存在零点?

生:不一定,可用二次函数说明.

② 若函数f(x)存在零点,是否一定有f(a)·f(b)<0?

生:不一定,如图3,f(x)在区间(a,b)内有两个零点,但f(a)·f(b)>0.

4.数学应用

例2已知函数y=f(x)在区间[-2,3]上的图象不间断,则由表1可知,函数f(x)在(-2,3)上有______个零点.

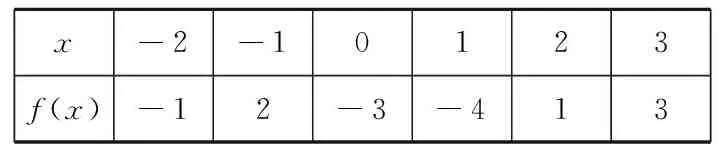
表1

生:函数f(x)在(-2,3)上至少有3个零点.因为函数y=f(x)在区间[-2,3]上的图象不间断,且f(-2)·f(-1)<0,所以在区间(-2,-1)上至少有1个零点,同理,在区间(-1,0)和(1,2)上都至少各有1个零点.

例3口答下列函数是否存在零点:

(1)f(x)=x2-2x-1,x∈(2,3);

(2)f(x)=x3-4x-1,x∈(1,3);

(3)f(x)=x3-4x-1,x∈(-2,0).

生:第(1)问,f(2)<0,f(3)>0,存在零点；第(2)问,f(1)<0,f(3)>0,存在零点；第(3)问,f(-2)<0,f(0)<0,不存在零点.

师:第(3)问,是这样吗?再想想.

生:f(-1)>0,存在零点.

师:至少存在几个零点?

生:2个,分别在区间(-2,-1),(-1,0)上.

例4设函数f(x)=2x+mx-4.

(1)当m=1时,试问f(x)有几个零点?

(2)当m=-1时,试问f(x)有几个零点?

生:第(1)问,容易知道f(x)=2x+mx-4是R上的增函数,所以f(x)=0有解,f(x)有零点.

师:可以这样说明吗?

生:哦,又因为f(1)<0,f(2)>0,所以f(x)有唯一零点.

师:对于第(2)问,f(x)=2x-x-4在R上不单调,怎么处理?

生:画图.

师:怎么画图?

生:在同一坐标系中,画出函数y=2x和y=x+4的图象.

师:你能说说零点的大致范围吗?

生:由函数图象知有2个零点,记为x1,x2(x10,f(2)<0,所以x2∈(2,3).又f(-4)>0,f(-3)<0,所以x1∈(-4,-3).

师:如果要让x2更精确一点怎么办?

生:取中间数2.5.

师:再精确.

生:再取中间数.

师:这其实就是后面要学习的二分法.先由图判断大致范围,再结合计算.形有直观功能,而数可以入微,具体估算出范围.

5.疑难化解

例5试将下列函数零点限定在相邻的两个整数之间.(板演)

(1)f(x)=2x-x-1;

(2)f(x)=x-lgx-3.

学生发现不宜利用函数单调性解决,受例4启发，将第(1)问中f(x)=2x-x-1的零点问题转化化归为函数y=2x与y=x+1图象公共点的问题,并正确画图解决.第(2)问类似.

议一议下列函数的零点个数：

(1)f(x)=x3-4x-1;

(2)f(x)=2x-x2.

学生独立思考与分组讨论相结合,由小组代表画图并发言.学生经过努力，正确完成第(1)问.第(2)问由于图象偏差,仍然遗漏零点,教师指出后用几何画板作演示.

师:请同学们进行自我小结.

思考:函数f(x)=xln(x+1)-2的零点个数.(留作课后思考题)

二、几点思考

1.以生为本,重视学生的课堂参与

学生是数学学习的主人,课堂教学应凸显学生的主体地位,重视学生的课堂参与.这种参与不是形式上表面化的参与,而是富有数学意义的思维参与.

纵观整节课可以发现,虽有教师的问题预设,以及必要的诱导点拨,但更多的是学生的思考探索和交流表达.从零点探求和定理探究环节来看,学生经历了定理的生成、发展和完善的过程,这不仅有助于领悟零点存在性定理的本质,而且还有助于培养学生勇于探索、敢于质疑、善于反思的科学态度和理性精神.对于一些较难的例题,教师仍能从容不迫,给予学生思考的时间,鼓励学生开口表达,动手操作实践,在思考、交流、表达的过程中积累数学活动经验,提升数学学科素养.

2.问题驱动,聚焦问题的深度思考

众所周知,问题是数学的心脏,数学教学应该围绕数学问题展开,促使学生聚焦数学问题深度思考.因此,精心设计好的数学“问题链”显得尤为重要.

纵览各个教学环节,课堂教学始终围绕数学问题展开.教师以凝练的语言,提出问题,并适时追问和反问.以例题教学来看,问题设计简洁有力、层层递进,形成系列“问题链”.例2与例3前2问可以深化对零点存在性定理的基本理解,从例3第(3)问开始拓展延伸,要求逐步提高,对学生的思维提出了较高的挑战.从课堂表现来看,问题设计恰到好处,教师关键处适时点拨,能够有效促进学生的深度思考.

3.探究引领,彰显深度思考的思维价值

根据任务设计的思维价值,可以把数学教学划分为三种水平,即记忆、解释性理解和探究性理解.数学教学应设计与实施探究性任务,彰显数学探究的思维训练价值.

以零点存在性定理的探究为例.如果直接告知学生,再利用习题巩固,那么教学就停留于记忆层次;如果学生思考不足,就提出定理,给予解释,那么教学就止步于解释性理解层次.本节课,教师以定理探究为引领,从一次函数零点存在性的判定切入,搭建“脚手架”,再自然地推广到任意函数,最后要求学生组织语言形成定理.整个教学环节,由特殊到一般,学生在主动探究中获得了定理,提升了素养.这样的探究活动,是真探究,彰显了数学探究的思维训练价值.

当然,从一定意义上来说，教学也是遗憾的艺术.这节课由于时间原因,在收尾环节略显仓促,否则教学效果应该更好.此外,由于教学对象是学校的一个实验班,具有较强的学习能力.因此,对于数学能力层次较低的教学对象,是否能采用这样的教学方式,尚需进一步探讨.