极坐标与参数方程问题的分类研究*

杨春猛 文 萍

(云南省玉溪市红塔区教育科学研究所,653100) (云南省玉溪师范学院数学与信息技术学院，653100)

“极坐标与参数方程”是高中数学选修4-4的重要内容,也是高考选考内容的考点之一.本文结合典型例题,研究不同类型的解题策略.

一、参数方程表示点的问题

参数方程是以参变量为中介来表示曲线上点的坐标的方程,是曲线在同一坐标系下的另一种表示形式.自然而然,参数方程就具有“点的本质”.从这个角度出发,可以把参数方程中与点有关的问题归纳为三类问题来研究:

1.点到点的距离问题

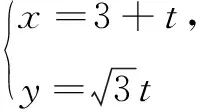
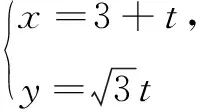
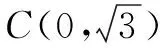
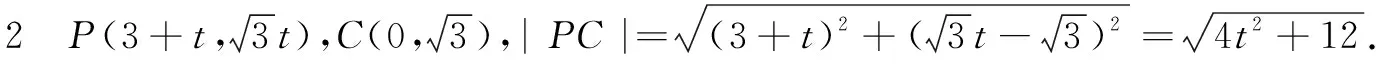
∴t=0时,|PC|最小,此时P(3,0).

评析第(2)问的解法1,使用了点到直线的距离公式求解,比较符合学生的思维习惯.但这里需要求两点间距离最小时的点P的坐标,就得先求出过圆心且垂直于直线l的方程,再联立求解,比较麻烦.如果理解了参数方程是以参变量为中介来表示曲线上点的坐标的方程,就能想到解法2,简洁迅速地解决问题.

2.点到直线的距离问题

例2在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为

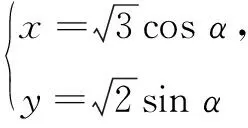
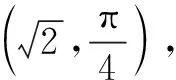
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.

解析(1)略.

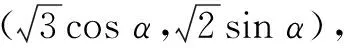
评析第(2)问是把参数方程看作点的坐标的典型问题,很自然地想到使用点到直线的距离公式.

3.点的轨迹方程问题

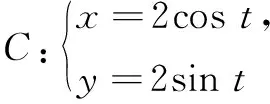
(1)求M的轨迹的参数方程；

(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.

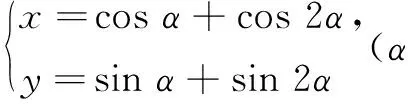
评析第(1)问是点的轨迹的问题,t=α时表示动点P,t=2α时表示动点Q,M为PQ的中点,使用中点坐标公式就可以解决问题,这源于参数方程表示点,反之,点也可以表述为参数方程的形式.第(2)问的距离d是点M到坐标原点的距离,自然地使用两点间距离公式就可以了.

二、直线参数方程的几何意义问题

1.标准的直线参数方程问题

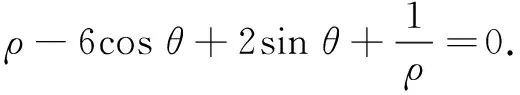
(1)写出曲线C的直角坐标方程和直线l的参数方程;

(2)设l与曲线C相交于A,B两点,求|AB|的值.

解析(1)曲线C化为ρ2-6ρcosθ+2ρsinθ+1=0,化为直角坐标方程为x2+y2-6x+2y+1=0,化为标准方程为(x-3)2+(y+1)2=9,

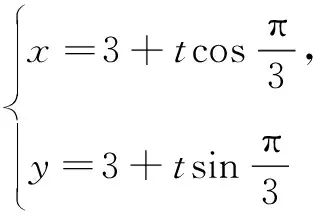
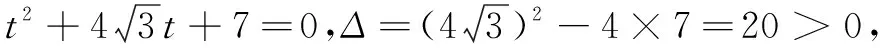
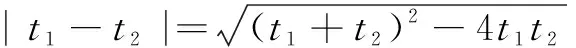
2.非标准的直线参数方程问题

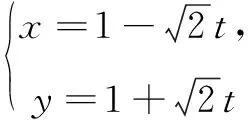
(1)说明C2是哪种曲线,并将C2的方程化为普通方程;

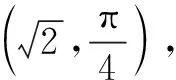
解析(1)略.

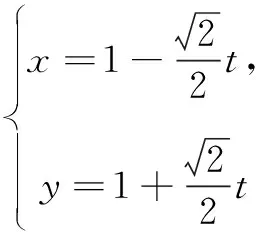
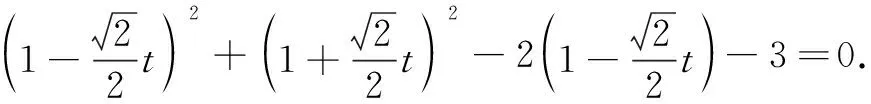
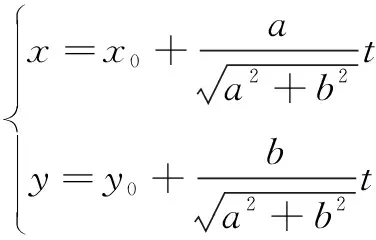
三、极坐标中ρ的几何意义问题

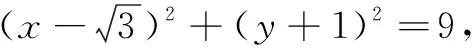
(1)求圆C的极坐标方程;

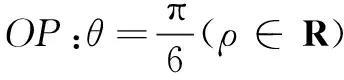
解析略.

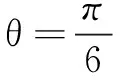
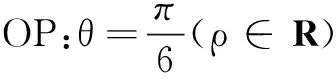
评析第(2)问因为直线过原点,所以解法1直接使用极坐标中极径ρ的几何意义；解法2则是使用直线参数的几何意义另外一个角度,直线过了定点(原点),根据题型的分析可知,故可以考虑使用直线参数的几何意义来解决.

综上所述,极坐标与参数方程可以归纳总结为四类问题来研究,分别是相互转化的问题、参数方程点的本质的问题、直线参数方程中参数的几何意义问题,极坐标中极径的几何意义问题,可以简记为: “相互化，点本质，定点t，原点ρ”.