站在学生的角度践思数学抽象

韩乃芳

[摘  要] 教师要站在学生学的角度，去思考核心素养如何落地这个问题. 站在学生的角度，意味着教师教学研究视角的切换，意味着教师要更多地思考学生如何学才能保证核心素养落地. 数学抽象是数学思维的产物，数学抽象的过程是一个逻辑建构的过程. 观察学生的数学抽象过程与结果，结合结果去判断学生在数学抽象过程中是怎样进行逻辑建构的，是重要的站在学生角度践思数学抽象策略.

[关键词] 高中数学;学生视角;数学抽象

在高中数学教学中，核心素养培育的要求，使得教师要更多地思考应当通过什么样的途径，来保证核心素养的落地. 从当前的研究来看，教师的研究重心更多地落在自身的努力上，即总是思考如何通过“教”的优化，去实现教学过程的优化，从而实现核心素养落地. 这是必要的同时又是不够的，笔者以为教师还要站在学生的角度，去思考核心素养如何落地这个问题. 站在学生的角度，意味着教师教学研究视角的切换，意味着教师要更多地思考学生如何学才能保证核心素养落地. 这从逻辑上是讲得通的，因为核心素养强调的是学生应当具备的能够适应社会发展与终身发展的必备品格与关键能力. 既然是“学生应当具备的”，那自然就要关注学生的学习过程，关注学生学习过程最根本的方法，就是教师要建立学生的视角. 笔者在教学中尝试站在学生的角度去思考并实践核心素养培育，取得了一些收获. 本文以高中数学学科核心素养中的数学抽象为例，谈谈笔者的一些浅显的收获.

■站在学生的视角理解数学抽象

站在学生的视角理解数学抽象是非常必要的，“数学在本质上研究的是抽象了的东西”，这启示数学教师在教学中要再现抽象过程，不能将数学知识直接“抛”给学生，让学生死记知识、模仿练习来学数学. 相反，教师在教学中要设计符合学生认知规律的教学，要从学生身边已有的经验抽象出数学，要让学生经历数学抽象生成的过程，体会这个过程中伴随的数学思想. 具体来说，在学生视角下的数学抽象，应当有这样两点理解：

第一，数学抽象是数学思维的产物. 数学抽象的过程一定是数学思维的过程，学生运用数学思维去加工学习的对象，将其中非数学因素剥离，只留下与数学相关的要素，这就是一个数学抽象的过程. 在这个过程中，无论是非数学因素的剥离，还是剩余数学元素的重新建构，都与数学思维有关，而且这样的一个思维过程是学生运用已有的数学概念、规律，对学习对象进行加工的过程.

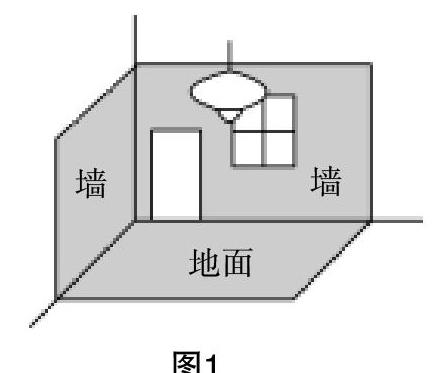
举一个例子，对于“空间直角坐标系”的学习，可以让学生经历一个数学抽象的过程，最简单的如让学生去分析一个由三张墙面相交的墙角，可以将墙角抽象为一个“点”，将三张墙面两两相交所形成的线抽象为“坐标轴”，去除墙面这一非数学要素，留下的就是一个由点与坐标轴组成的空间直角坐标系的雏形.

这就是一个非常简单的数学抽象过程，这样的过程中，学生的思维是不可或缺的，而数学抽象的结果自然也就是思维的产物.

第二，数学抽象的过程是一个逻辑建构的过程. 在日常的教学中，很少有人将数学抽象与逻辑建构结合起来，更多的人认为数学抽象是一个经验作用的过程但是根据徐利治教授等专家的研究发现，数学抽象的过程本质上是数学学习者基于一定的逻辑来建立或者构造新的数学对象的过程. 这是一个非常有意义的判断，这一判断意味着数学抽象超越了经验理解，更多的具有数学意味，又或者说如果离开了逻辑与建构，数学抽象是难以真正发生的.

比如上面的例子当中，从生活中的墙角抽象出空间直角坐标系，是一个剥离非数学因素的过程，而判断哪些因素是非数学因素，需要学生已有的数学知识基础与逻辑参与. 比如学生在平面直角坐标系的学习中，已经认识到要建立一个直角坐标系，需要的是原点和坐标轴，那么在研究墙角这一生活事物时，自然就会留下点和坐标轴两个数学要素，而剥离其他与直角坐标系无关的因素. 这个过程中的逻辑其实还是非常清晰的，而要培养学生的数学抽象素养，是不能忽视这一逻辑的，也是不能忽视这一逻辑建构过程的.

需要再次强调的是，这两点理解都是在学生的视角下建立的，教师在教学中有了学生的视角，才能真正急学生之所急，想学生之所想，才能让自己的教学更加符合学生的学习需要.

■站在学生的角度体验数学抽象

综合上面的分析，可以发现抽象是数学的思维方式之一，也是数学活动中最基本的思维方法.对于数学抽象的教学，实际上是一种构造活动，是借助于旧知和推理进行的逻辑建构，形成新概念或定理的活动. 而结合笔者在教学实践中的一些努力，发现站在学生的视角去理解数学抽象，还只是一个间接的过程. 教师要想有更加直接的体验，那就应该站在学生的角度去体会数学抽象过程. 体验学生的数学抽象过程，说起来简单做起来却不容易，其中的一个关键就是要知道学生在数学抽象的过程中是怎么想的. 对于这个问题的解决，笔者采用的方法是观察学生的数学抽象过程与结果，结合结果去判断学生在数学抽象过程中是怎样进行逻辑建构的.

例如，在上面所举的“空间直角坐标系”这一例子当中，部分学生对空间直角坐标系的理解，实际上是在他人研究的基础上形成的，对于这部分学生而言，其实缺少直接的经验. 考虑到班级授课制的特点，这个时候教师实际上是不可能将上述教学过程重复的，更有价值的做法应当是在对空间直角坐标系的应用当中，继续完成数学抽象的过程. 一个简单的做法就是：假如要确定房间内某一个白炽灯的位置（如图1），那应当需要什么样的序数组？（考虑到思维的层次性，教师在这里可以用一个平面直角坐标系的例子来辅助学生去理解，限于篇幅，这里不再赘述）

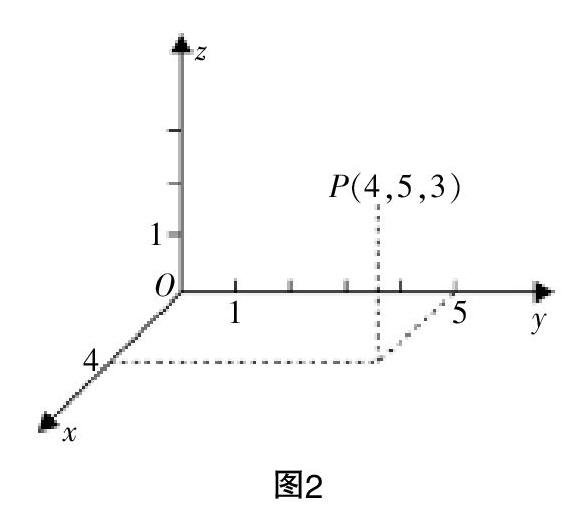
学生在解决这个问题的时候，同样要经历一个数学抽象的过程，笔者注意到学生能够结合上一个教学环节，先迅速地将该生活问题转变为数学问题——实际上也就是重复一个空间直角坐标系的形成过程. 待到空间直角坐标系形成之后，学生会用一个点去表示灯泡所在的位置，其后学生产生的问题自然就是：在空间直角坐标系里这个点的坐标是什么？——在参与多个小组讨论的过程中，笔者都注意到学生能够自发地提出这一问题. 这个问题的提出实际上是建立在前一抽象的基础之上的（同时也有着逻辑推理的参与，这是数学学科核心素养中的另一个要素，这里不展开阐述）;而且这一问题的提出意味着学生大脑中的表象已经可以用另一个图来表示（如图2）. 如果这个图在学生大脑中是清晰的，那就说明学生的数学抽象过程是成功的. 事实上，教师还可以进一步跟踪学生的思维，比如看学生能否根据图迅速准确地判断出P点的坐标.

在這样的一个教学过程中，教师立足于学生的学习过程，通过学生的学习结果去反推学生在数学抽象过程中的具体思路，以及可能遇到的障碍，这样教师就能对学生的数学抽象过程会感同身受，同时这样的体验也可以为教师的教提供更加精准的方向.

■站在学生的角度反思数学抽象

数学抽象是数学学科核心素养的第一要素，而数学核心素养是数学课程改革的新指向，是数学教育的培养目标. 基于对高中数学课程中数学核心素养六个维度的理解，强调依靠数学抽象过程生成数学抽象核心素养，是高中数学教师对核心素养最基本的理解.

笔者在实际教学中以数学抽象作为突破口，是考虑到以教学形态出现的数学抽象，遵循数学抽象的一般规律. 而进一步的研究表明，数学抽象具有实物抽象、半符号抽象、符号抽象和形式化抽象四种表现形式，这为数学分层教学的实施提供了数学学科前提和思维训练的教育基础. 笔者以为，高中数学教学中数学抽象的重点是后面三种表现形式，而实物抽象更多地发挥着帮助学生建立表象（即思维对象）的作用.

结合上面空间直角坐标系的例子可以发现，第一次建立空间直角坐标系的时候，实物抽象的过程比较明显，而在第二次进行灯泡位置确定的时候，就已经进入了半符号抽象和符号抽象的阶段. 所以这样的两个过程，虽然都是数学抽象，但是有所不同. 同时这样的设计又是有道理的，因为这是一个循序渐进的过程，从实物抽象到半符号抽象以及符号抽象，正好能够让几乎所有的学生都建立一个比较丰富的数学抽象过程，待到学生对空间直角坐标系比较熟悉之后，学生如果再次遇到空间直角坐标系，那就进入了形式化抽象的阶段. 所以站在学生的角度反思数学抽象素养的培育，教师要有循序渐进的思路，必要的时候还需要分层次教学，这样才能让不同层次的学生与数学抽象的不同形式进行高效的匹配，从而达成核心素养培育的效果.