优化解题过程，提升计算能力

孙世林

[摘  要] 历年高考解析几何解答题，综合性强，能力要求高，考生普遍失分较多. 文章以一道解析几何问题为例，谈谈如何回归解析几何知识本质，如何优化解题过程，如何从多角度探究问题，从而提升计算能力.

[关键词] 解析几何;解题思路;运算求解

解析几何综合题是考查学生能力的主要内容之一，在高考中占有重要地位， 试题呈现出综合性强，难度大，灵活多变的特点，对能力要求高，普遍存在解题思路不清、方法选择不当、计算不过关等现象，下面就谈谈如何优化解题过程，提升计算能力.

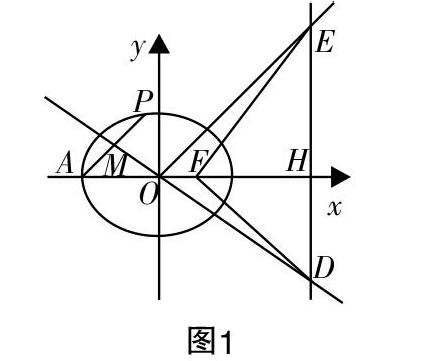
问题：如图1，已知椭圆C：■+■=1（a>b>0）的离心率为■，F为椭圆C的右焦点，A（-a，0），AF=3.

（Ⅰ）求椭圆C的方程;

（Ⅱ）设O为原点，P为椭圆上一点（点P不是椭圆的长轴端点），AP的中点为M.直线OM与直线x=4交于点D，过O且平行于AP的直线与直线x=4交于点E，

求证：∠ODF=∠OEF.

思路1：本题的第一问比较简单，第二问是证明两个角相等.要想证明这两个角相等，我们先看这两个角是怎样形成的？P为椭圆上一点，AP的中点M与原点O连接并延长，与直线x=4相交，形成了点D，点E是过O且平行于AP的直线与直线x=4相交形成的，这样才出现了线段DF和EF，从而有了∠ODF与∠OEF，可见这两个角与点P有紧密的联系，所以可以从直线AP的方程或点P的坐标入手.

解法1：（Ⅰ）椭圆C的方程是■+■=1.

（Ⅱ）由（Ⅰ）得A（-2，0）.设直线AP的方程为：y=k（x+2）（k≠0），

将其代入椭圆方程，整理得（4k2+3）x2+16k2x+16k2-12=0，

显然，其Δ>0，设AP的中点M（x■，y■），P（x■，y■）.

所以-2+x■=■.

所以x■=■=■，y■=k（x■+2）=■，即M■，■.

所以直线OM的斜率是■=-■，

所以直线OM的方程是y=-■x. 令x=4，得D4，-■.

设直线OE的方程是y=kx.令x=4，得E（4，4k）.

由F（1，0），得直线EF的斜率是■=■，所以EF⊥OM.

又直线DF的斜率是■=-■，

所以DF⊥OE，

所以∠ODF=∠OEF.

解法2：（Ⅰ）椭圆C的方程是■+■=1.

（Ⅱ）由（Ⅰ）得A（-2，0）. 设P（x■，y■）（x■≠±2），其中3x■+4y■12=0.

因为AP的中点为M，所以M■，■.

所以直线OM的斜率是k■=■，

所以直线OM的方程是y=■x. 令x=4，得D4，■.

直线OE的方程是y=■x.令x=4，得E4，■.

由F（1，0），得直线EF的斜率是k■=■，

因为k■·k■=■·■=■=-1，

所以EF⊥OM.

同理可得k■·k■=■·■=■=-1，

所以DF⊥OE，

所以∠ODF=∠OEF.

評析：解析几何综合问题常在运动变化过程中探究某些不变的性质与规律，对于这类运动变化问题，解题时要从已知出发深入探究产生运动变化的根源，从产生运动变化的根源入手.解法一从直线AP的方程入手，解法二从点P的坐标入手，对比发现解法二运算量小，究其原因是因为本题运动变化的根源是点P，所以解题时要选择好是从直线方程入手，还是从点的坐标入手，这样就可以优化解题过程，减少计算量，自然快捷地解决此类问题.

思路2：本题的第二问是一道证明题，我们可以从结论出发反推成立的条件，若∠ODF和∠OEF相等，则它们的三角函数值就应该相等.我们选择哪种三角函数？如图不难发现∠ODF=∠ODH-∠FDH，而∠ODH和∠FDH分别位于Rt△ODH和Rt△FDH中，可见这些角的正切值很容易得到;同理∠OEF=∠OEH-∠FEH也容易求得正切值，这样我们就可以借助证明两个角的正切值相等来说明两个角相等.

解法3：（Ⅰ）椭圆的方程为■+■=1.

（Ⅱ）由解法2可知，D4，■，E4，■. 设直线x=4与x轴交于H，

设∠ODH=α，∠FDH=β，则tanα=■，tanβ=■;

所以tan∠ODF=tan（α-β）=■，同理，tan∠OEF=■.

依题意，y■，y■异号，不妨设y■>0，

所以■-■=■+■= ■.

又y■（y■+12）+y■（y■+12）=（y■+y■）·（y■·y■+12） =（y■+y■）■·■+12=（y■+y■）■+12.

又点P（x■，y■）在椭圆上，所以3x■+4y■-12=0，

所以（y■+y■）■+12=（y■+y■）·■+12=（y■+y■）（-12+12）=0.

所以tan∠ODF=tan∠OEF，

依题意∠ODF和∠OEF均为锐角，所以∠ODF=∠OEF.

评析：解决解析几何综合问题时，有时直接求解，常常感觉不知从何入手，我们可以尝试从结论入手，本解法中我们借助证明两个角的正切值相等来说明两个角相等，这就实现了由几何条件向代数运算的转化，体现了解析几何的本质;几何条件代数化的途径很多，如本题我们也可以求出三角形的三边借助余弦定理求角的余弦值，也可以借助向量的数量积求角的余弦值，选择哪种途径要依据题目的特点，要有利于接下来的代数运算.

思路3：在解决解析几何的综合题时，要善于将问题进行转化，从多个角度，用不同的方法探究同一个问题，对于本题我们还可以继续深入探究题目中图形的几何特征，从几何角度寻求突破.本题是证明两角相等，观察图形发现，两个角分别位于有公共边OF的两个三角形中，由此可以联想到三角形的外接圆，联想有公共弦的两个圆，如果这两个圆的半径相等，那么其公共弦所对圆周角相等，这样我们便有了本题的第4种解法：

解法4：由解法一可知得D4，-■，E（4，4k）.

设过O，E，F三点的圆C■的方程为x2+y2+m■x+n■y+p■=0，将O，E，F代入圆的方程得：p■=0，m■=-1，n■=-4k-■，所以，圆C■的半径为r■=■（m■+n■-4p■）=■1+-4k-■■.

设过O，D，F三点的圆C■的方程为x2+y2+m■x+n■y+p■=0，将O，D，F代入圆的方程得：p■=0，m■=-1，n■=4k+■，

所以，圆C■的半径为r■=■（m■+n■-4p■）=■1+4k + ■■，可见，圆C■，C■有公共弦且半径相等，

所以∠ODF=∠OEF.

点评：“解析几何”研究的是几何问题，恰当利用平面几何的有关知识解决问题，也是不可或缺的方法，解析几何问题中蕴含很多几何条件，这些几何条件间有什么关系？从这些几何关系出发又能得到什么样的新的几何关系？某些几何关系成立需要有怎样的几何条件？随着这些疑问的探究和解决，解题思路也就自然生成了.